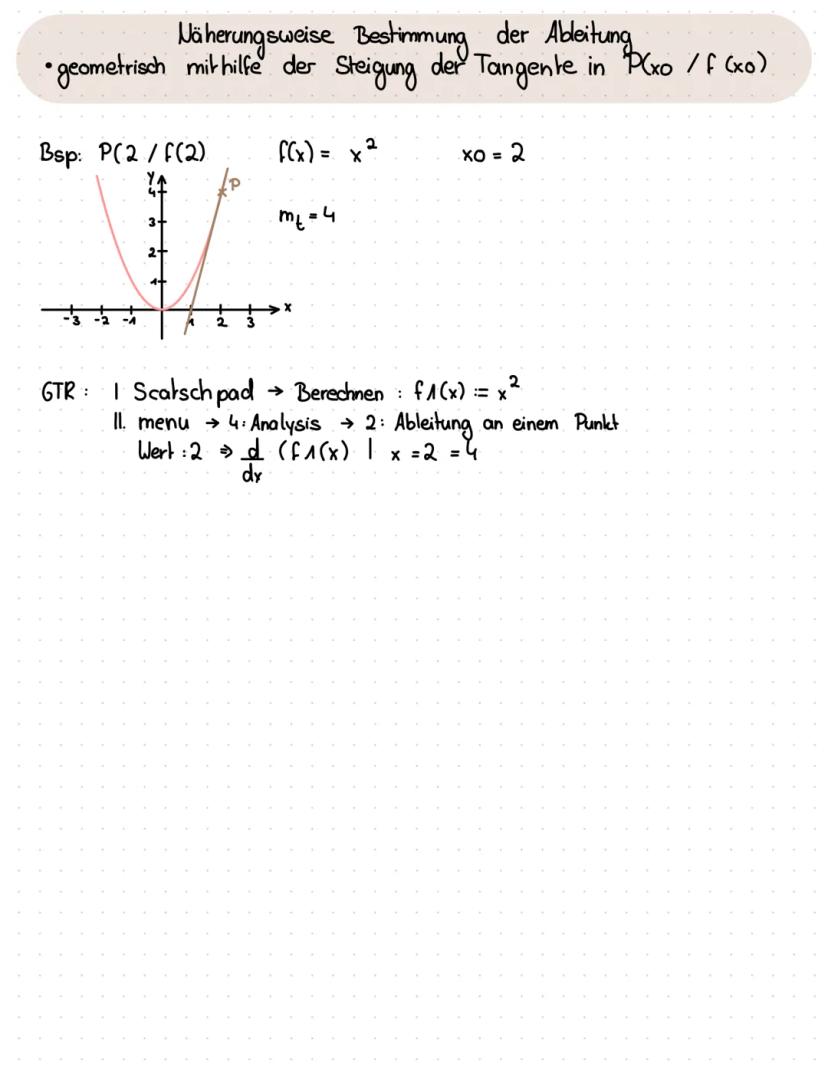
- Näherungsweise Bestimmung der Ableitung —> h-Methode —> geometrishce Mithilfe der Steigung der Steigung der Tangente in P(x0/f(x0) - Ableitung an einer bestimmten Stelle berechnen - Ableitungsfunktionen - Tangeten - Ableitungen
Melde dich an, um den Inhalt freizuschaltenEs ist kostenlos!
Zugriff auf alle Dokumente
Verbessere deine Noten
Werde Teil der Community
Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie