Grundlagen der Funktionen

Lineare Funktionen kennst du bereits gut: y = mx + t. Die Steigung m berechnest du mit Δy/Δx oder über den Tangens des Winkels. Parallele Geraden haben die gleiche Steigung, senkrechte Geraden haben Steigungen, die sich zu -1 multiplizieren.

Bei quadratischen Funktionen f(x) = ax² + bx + c findest du Nullstellen mit der Mitternachtsformel: x₁,₂ = $-b ± √(b²-4ac)$/(2a). Der Scheitelpunkt liegt bei xs = -b/(2a).

Polynome sind Funktionen mit verschiedenen Potenzen von x. Je nach Vielfachheit der Nullstellen verhält sich der Graph unterschiedlich: einfache Nullstellen schneiden die x-Achse, doppelte berühren sie nur, dreifache bilden Terrassenpunkte. Ein Polynom ist achsensymmetrisch, wenn alle Potenzen gerade sind, und punktsymmetrisch bei ungeraden Potenzen.

Merktipp: Die Mitternachtsformel heißt so, weil du sie um Mitternacht aus dem Schlaf geweckt aufsagen können solltest!

Trigonometrische und rationale Funktionen

Trigonometrische Funktionen wie sin(x) und cos(x) sind periodisch. Die Cosinus-Funktion ist achsensymmetrisch mit Nullstellen bei x = π/2 + kπ, die Sinus-Funktion ist punktsymmetrisch mit Nullstellen bei x = kπ.

Für Funktionsterme der Form a·sin(bx) + c gilt: b = π/Periode, a bestimmt die Amplitude und c die Verschiebung nach oben oder unten.

Gebrochen-rationale Funktionen haben die Form f(x) = Zählerpolynom/Nennerpolynom. Nullstellen findest du im Zähler, Polstellen entstehen, wenn der Nenner null wird. Bei Polstellen 1. Art (ungerade Vielfachheit) wechselt das Vorzeichen, bei Polstellen 2. Art (gerade Vielfachheit) nicht.

Wichtig: Der Nenner darf niemals null werden - das sind die Stellen, die aus dem Definitionsbereich ausgeschlossen werden müssen!

Asymptoten und Exponentialfunktionen

Asymptoten beschreiben Geraden, denen sich Funktionen annähern. Senkrechte Asymptoten entstehen bei Polstellen, waagrechte Asymptoten abhängig vom Grad: Nennergrad > Zählergrad führt zu y = 0, gleiche Grade zum Verhältnis der Vorfaktoren.

Schräge Asymptoten gibt es, wenn der Zählergrad größer als der Nennergrad ist. Hebbare Definitionslücken entstehen, wenn sich Faktoren kürzen lassen.

Die e-Funktion ist die am schnellsten wachsende Funktion mit besonderen Eigenschaften: Sie hat keine Nullstellen, die x-Achse ist waagrechte Asymptote und sie ist ihre eigene Ableitung. e ≈ 2,71 ist eine wichtige mathematische Konstante.

Eselsbrücke: Die e-Funktion ist wie ein Energydrink unter den Funktionen - sie wächst explosionsartig schnell!

Logarithmus und Funktionsmodellierung

Die ln-Funktion ist die Umkehrfunktion der e-Funktion und die am langsamsten wachsende Funktion. Sie ist nur für positive x-Werte definiert, hat eine Nullstelle bei x = 1 und eine senkrechte Asymptote bei x = 0.

Funktionsmodellierung funktioniert nach dem Schema af$b(x+c)$+d: c verschiebt horizontal, d vertikal, a streckt/staucht vertikal und spiegelt bei negativen Werten, b wirkt horizontal.

Nullstellen findest du, indem du f(x) = 0 setzt. Bei quadratischen Funktionen verwendest du die Mitternachtsformel, bei anderen Funktionen klammerst du oft aus. Den y-Achsenabschnitt erhältst du durch f(0).

Tipp: Bei der Funktionsmodellierung denkst du am besten von innen nach außen: erst die Klammer, dann Streckungen, dann Verschiebungen!

Schnittpunkte und Definitionsbereiche

Schnittpunkte zweier Funktionen findest du, indem du f(x) = g(x) setzt, nach x auflöst und dann den y-Wert berechnest. Das kann zu quadratischen Gleichungen führen, die du mit der Mitternachtsformel löst.

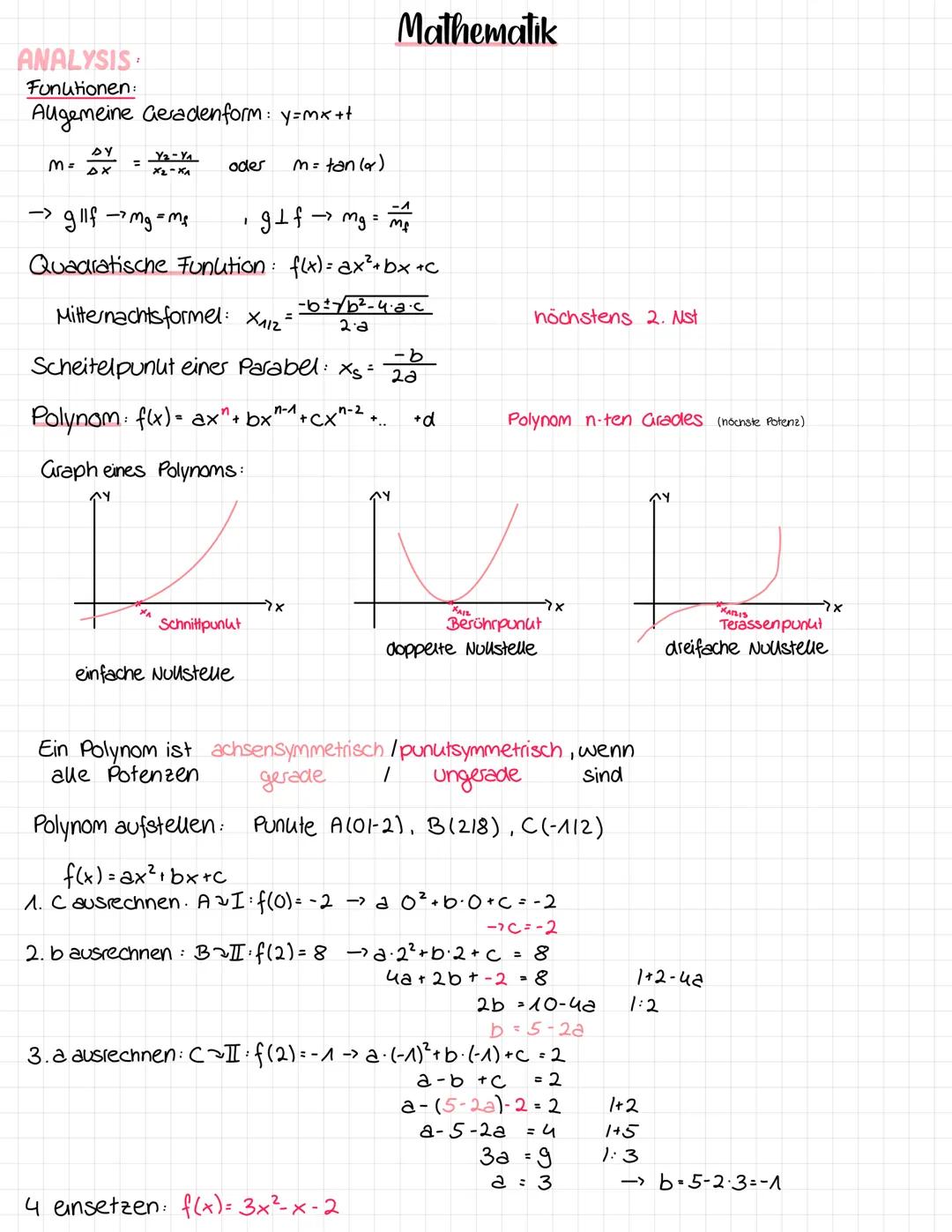
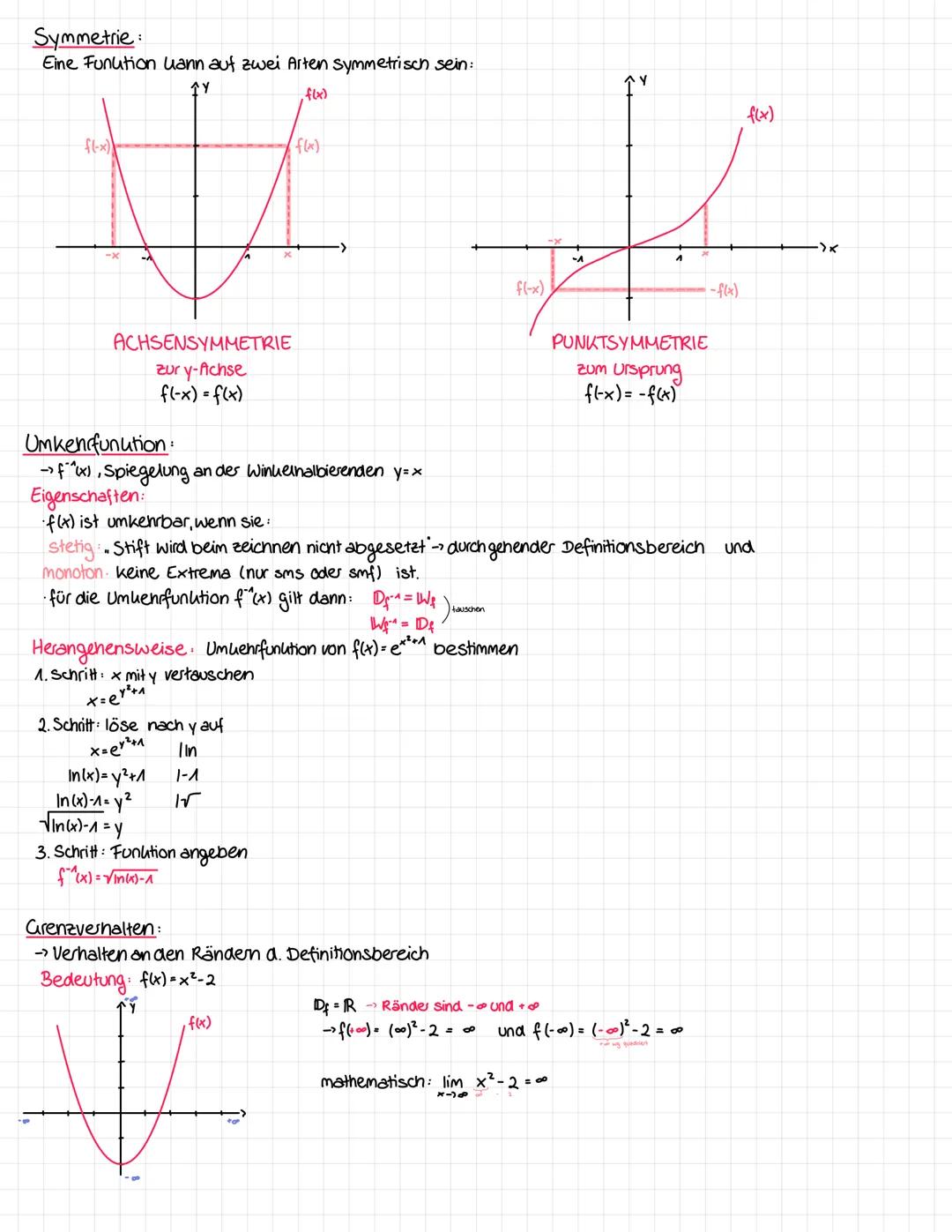
Der Definitionsbereich D umfasst alle x-Werte, für die eine Funktion definiert ist. Der Wertebereich W alle möglichen y-Werte.

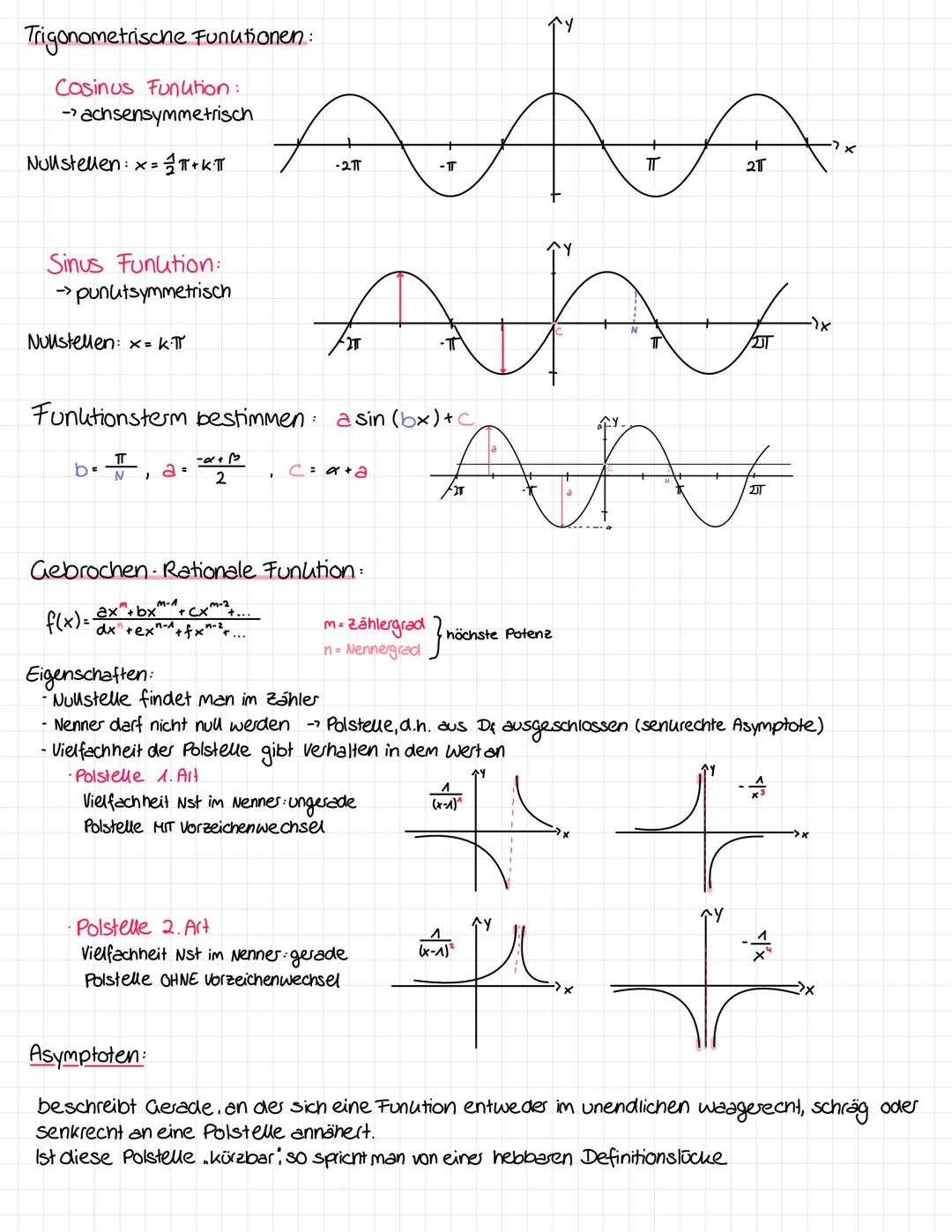
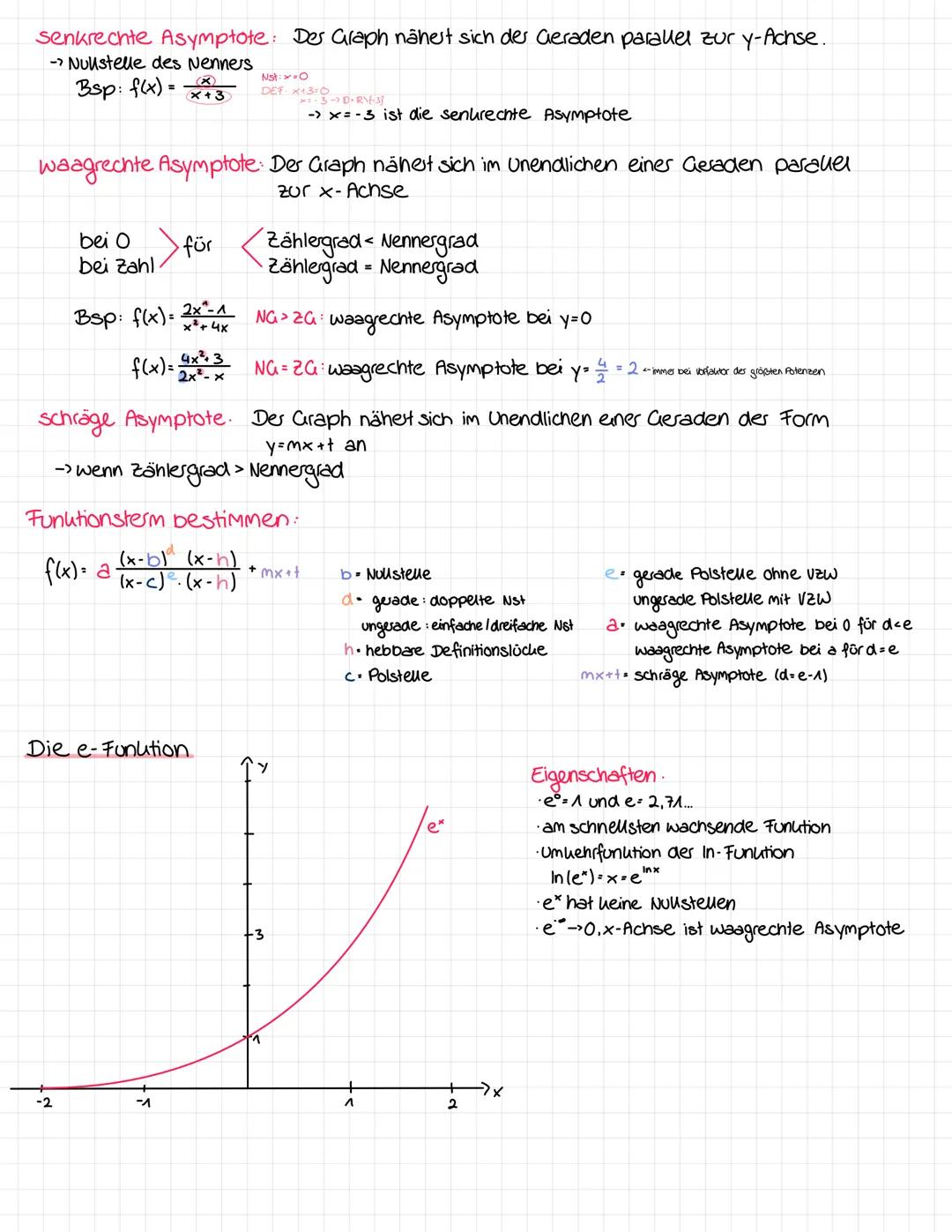
Wichtige Einschränkungen: Bei Brüchen darf der Nenner nicht null sein, bei Wurzeln muss der Radikand ≥ 0 sein, bei Logarithmen muss das Argument > 0 sein.

Die Herangehensweise ist immer gleich: Problematische Terme identifizieren, Bedingungen aufstellen und lösen. Bei der e-Funktion im Nenner setzt du ex - 1 = 0, was zu x = 0 führt.

Merkhilfe: Denk an die "Verbotsschilder" der Mathematik: Teilen durch null, Wurzel aus negativen Zahlen, Logarithmus von null oder negativen Zahlen!

Symmetrie und Umkehrfunktionen

Achsensymmetrie zur y-Achse erkennst du an f$-x$ = f(x), Punktsymmetrie zum Ursprung an f$-x$ = -f(x). Bei Polynomen: alle geraden Potenzen = achsensymmetrisch, alle ungeraden = punktsymmetrisch.

Umkehrfunktionen f⁻¹(x) entstehen durch Spiegelung an der Winkelhalbierenden y = x. Eine Funktion ist umkehrbar, wenn sie stetig und monoton ist. Dabei gilt: Df⁻¹ = Wf und Wf⁻¹ = Df.

Zum Bestimmen der Umkehrfunktion tauschst du x und y, löst nach y auf und schreibst das Ergebnis als f⁻¹(x).

Grenzverhalten beschreibt, was an den Rändern des Definitionsbereichs passiert. Du schreibst lim (x→∞) f(x) und bestimmst, ob das Ergebnis eine Zahl (waagrechte Asymptote) oder ±∞ ist.

Wichtig: Eine Funktion kann nur dann umgekehrt werden, wenn jeder y-Wert genau einmal vorkommt - sonst wäre die Umkehrung keine Funktion mehr!

Grenzwerte und Differentialrechnung

Bei gebrochen-rationalen Funktionen vergleichst du Zähler- und Nennergrad: NG > ZG führt zu lim = 0, NG = ZG zum Verhältnis der Vorfaktoren, NG < ZG zu ±∞.

Wichtige Grenzwerte: e^∞ → ∞, ln(∞) → ∞, ln(0) → -∞. Die Hierarchie lautet: e^x schlägt Polynome, Polynome schlagen Wurzeln, Wurzeln schlagen ln(x).

Die Differentialrechnung beschäftigt sich mit Änderungsraten. Die mittlere Änderungsrate ist m = $f(b)-f(a)$/$b-a$, die momentane Änderungsrate ist die erste Ableitung f'(x₀).

Die erste Ableitung f'(x) gibt die Steigung der Funktion an jedem Punkt an. Sie entsteht als Grenzwert des Differenzenquotienten.

Eselsbrücke: Die mittlere Änderungsrate ist wie deine Durchschnittsgeschwindigkeit, die momentane wie der Blick auf den Tacho in einem bestimmten Moment!

Ableitungsregeln und Extrema

Grundregeln: xⁿ wird zu n·xⁿ⁻¹, eˣ bleibt eˣ, ln(x) wird zu 1/x, sin(x) zu cos(x), cos(x) zu -sin(x).

Die Kettenregel wendest du bei verketteten Funktionen an: (u(v(x)))' = u'(v(x))·v'(x). Bei eᵛ⁽ˣ⁾ erhältst du eᵛ⁽ˣ⁾·v'(x).

Produktregel: (u·v)' = u'·v + u·v'. Quotientenregel: $u/v$' = $u'·v - u·v'$/v².

Extrema findest du, indem du f'(x) = 0 setzt. Wo die erste Ableitung positiv ist, steigt die Funktion (sms), wo sie negativ ist, fällt sie (smf). An Extremstellen wechselt das Monotonieverhalten.

Tipp: Bei der Kettenregel denkst du "äußere Ableitung mal innere Ableitung" - wie beim Zwiebelschälen von außen nach innen!

Tangenten, Wendepunkte und graphisches Ableiten

Tangenten sind Geraden, die eine Funktion in einem Punkt berühren. Ihre Steigung entspricht f'(x₀), die Gleichung lautet y = f'(x₀)·x + n. Den y-Achsenabschnitt n findest du, indem du den Berührpunkt einsetzt.

Wendepunkte liegen vor, wenn f''(x) = 0 ist und die Krümmung wechselt. Bei f'' > 0 ist die Funktion linksgekrümmt (Lächeln), bei f'' < 0 rechtsgekrümmt (Trauer). Wendepunkte haben maximale oder minimale Steigung.

Beim graphischen Ableiten überträgst du NEW-Stellen (Nullstellen, Extrema, Wendepunkte): Extrema von f werden zu Nullstellen von f', Wendepunkte von f zu Extrema von f'. Achsensymmetrische Funktionen werden zu punktsymmetrischen Ableitungen.

Das Newton-Verfahren nähert Nullstellen iterativ an: xₙ₊₁ = xₙ - f(xₙ)/f'(xₙ).

Merkregel: Links gekrümmt = lächeln = f'' > 0, rechts gekrümmt = traurig = f'' < 0!

Integralrechnung

Die Integralrechnung ist die Umkehrung der Differentiation. Eine Stammfunktion F(x) hat die Eigenschaft F'(x) = f(x).

Grundregeln: ∫xⁿ dx = xⁿ⁺¹/$n+1$ + c, ∫eˣ dx = eˣ + c, ∫1/x dx = ln|x| + c. Bei der linearen Kettenregel teilst du durch die innere Ableitung: ∫f$ax+b$ dx = 1/a·F$ax+b$ + c.

Das unbestimmte Integral ∫f(x) dx = F(x) + c gibt die allgemeine Stammfunktion an. Das bestimmte Integral ∫ₐᵇf(x) dx = F(b) - F(a) berechnet die Flächenbilanz zwischen x = a und x = b.

Flächenberechnungen zwischen zwei Funktionen: A = ∫ₐᵇ|f(x) - g(x)| dx. Erst Schnittpunkte bestimmen (Integrationsgrenzen), dann die Differenzfunktion integrieren.

Wichtig: Das bestimmte Integral gibt die Flächenbilanz an - positive und negative Flächen können sich aufheben! Bei echten Flächeninhalten brauchst du Betragsstriche.