Definitions- & Wertebereich verstehen
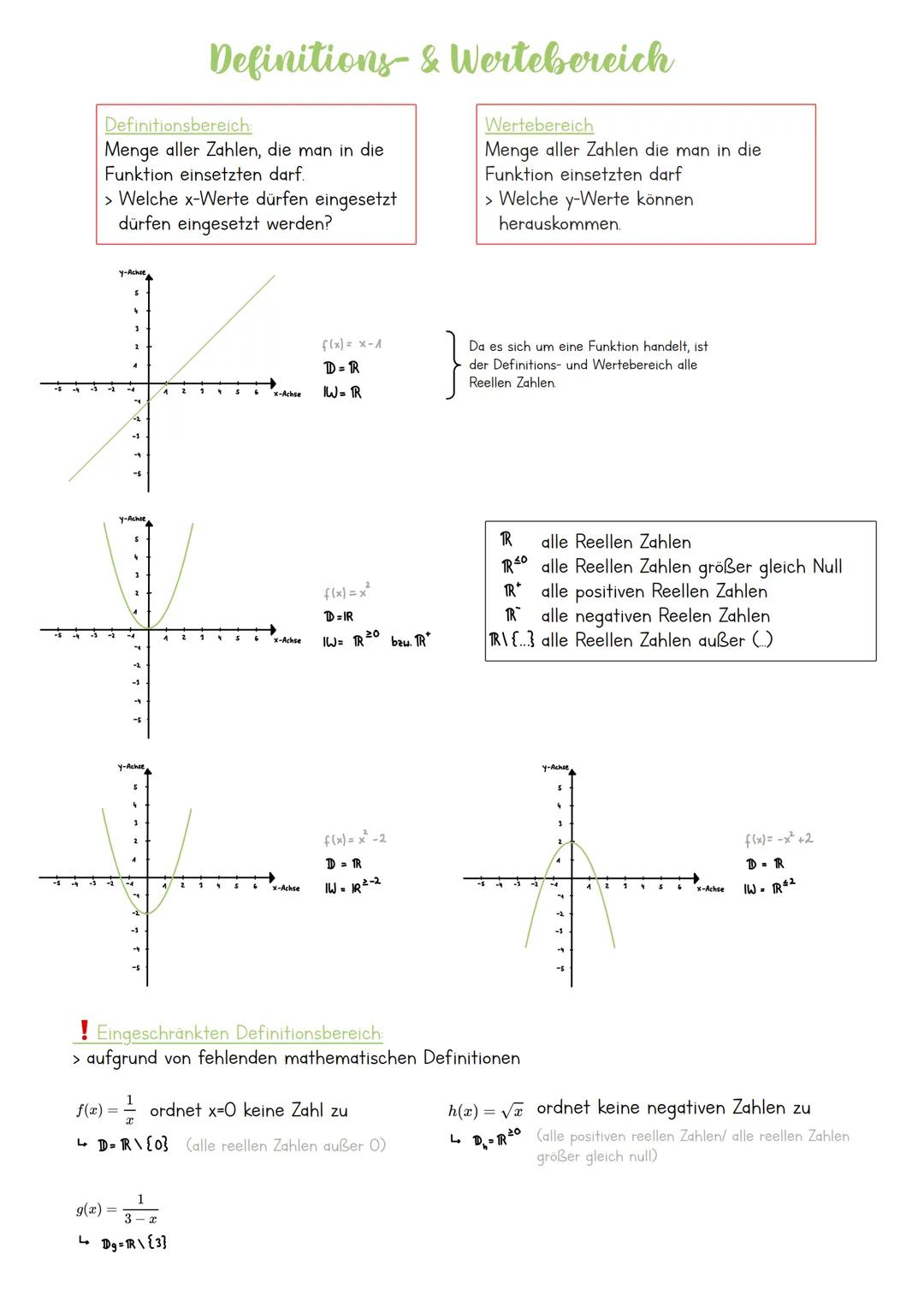
Der Definitionsbereich ist super einfach zu verstehen: Das sind alle x-Werte, die du in deine Funktion einsetzen darfst. Frag dich einfach: "Welche Zahlen kann ich für x verwenden, ohne dass etwas Unmögliches passiert?"
Der Wertebereich zeigt dir alle y-Werte, die als Ergebnis rauskommen können. Hier fragst du dich: "Welche Zahlen kann die Funktion überhaupt als Antwort geben?"
Bei einfachen Funktionen wie f(x) = x ist beides ℝ (alle reellen Zahlen). Du kannst jede beliebige Zahl einsetzen und kriegst auch jede beliebige Zahl raus.
Merktipp: ℝ = alle reellen Zahlen, ℝ⁰ = alle Zahlen ≥ 0, ℝ⁺ = nur positive Zahlen, ℝ⁻ = nur negative Zahlen, ℝ{0} = alle außer der Null
Quadratische Funktionen wie f(x) = x² haben immer den Definitionsbereich ℝ, aber der Wertebereich ist nur ℝ⁰, weil Quadrate nie negativ werden. Bei f(x) = x² - 2 verschiebt sich alles um 2 nach unten, also ist der Wertebereich ℝ≥-2.
Manchmal ist der Definitionsbereich eingeschränkt: Bei f(x) = 1/x darfst du keine Null einsetzen (Division durch Null geht nicht!), also ist D = ℝ{0}. Bei Wurzelfunktionen wie f(x) = √x sind nur positive Zahlen erlaubt, also D = ℝ⁰.