Fächer

Mathe

Funktionen und analysis

Kurvendiskussion einzelschritte

Grenzwert

E-Funktion einfach erklärt: Ableitungsrechner, Produktregel & Kettenregel

Name: Knowunity
Brand: Knowunity

Öffnen

E-Funktion einfach erklärt: Ableitungsrechner, Produktregel & Kettenregel

Carina

@carina_sophie

30 Follower

The document provides a comprehensive guide on E-Funktion (exponential function) and its applications in calculus, focusing on differentiation, integration, and growth models. It covers key concepts such as the Produktregel (product rule), Kettenregel (chain rule), and beschränktes Wachstum (limited growth). The guide offers detailed explanations, examples, and problem-solving techniques for students studying advanced mathematics.

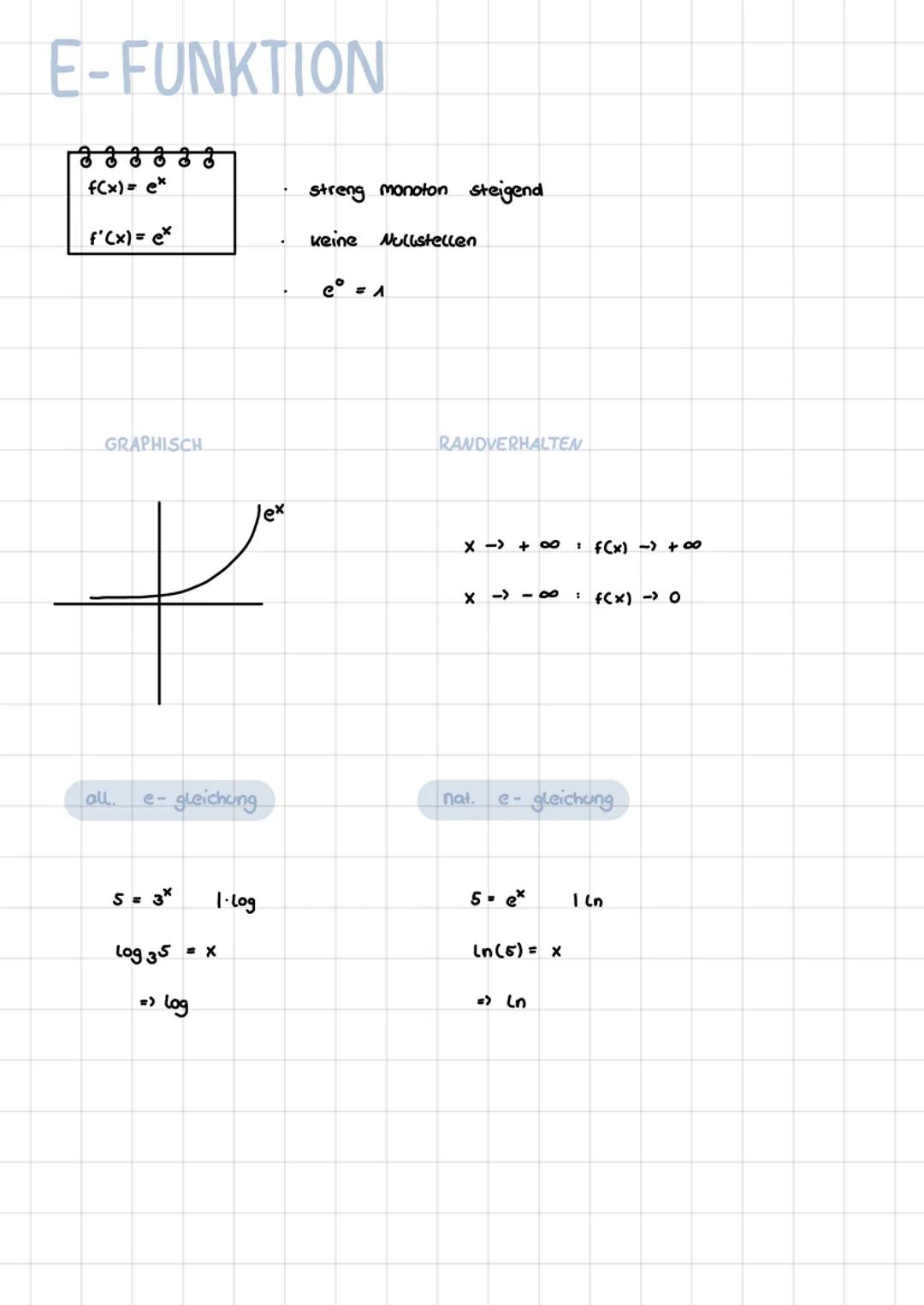
• The e-function is defined as f(x) = e^x, with its derivative being f'(x) = e^x.
• Various rules for differentiating e-functions are explained, including the product and chain rules.
• The guide covers finding zeros, y-values, intersection points, and analyzing function behavior.
• Integration techniques for e-functions are discussed, including improper integrals.
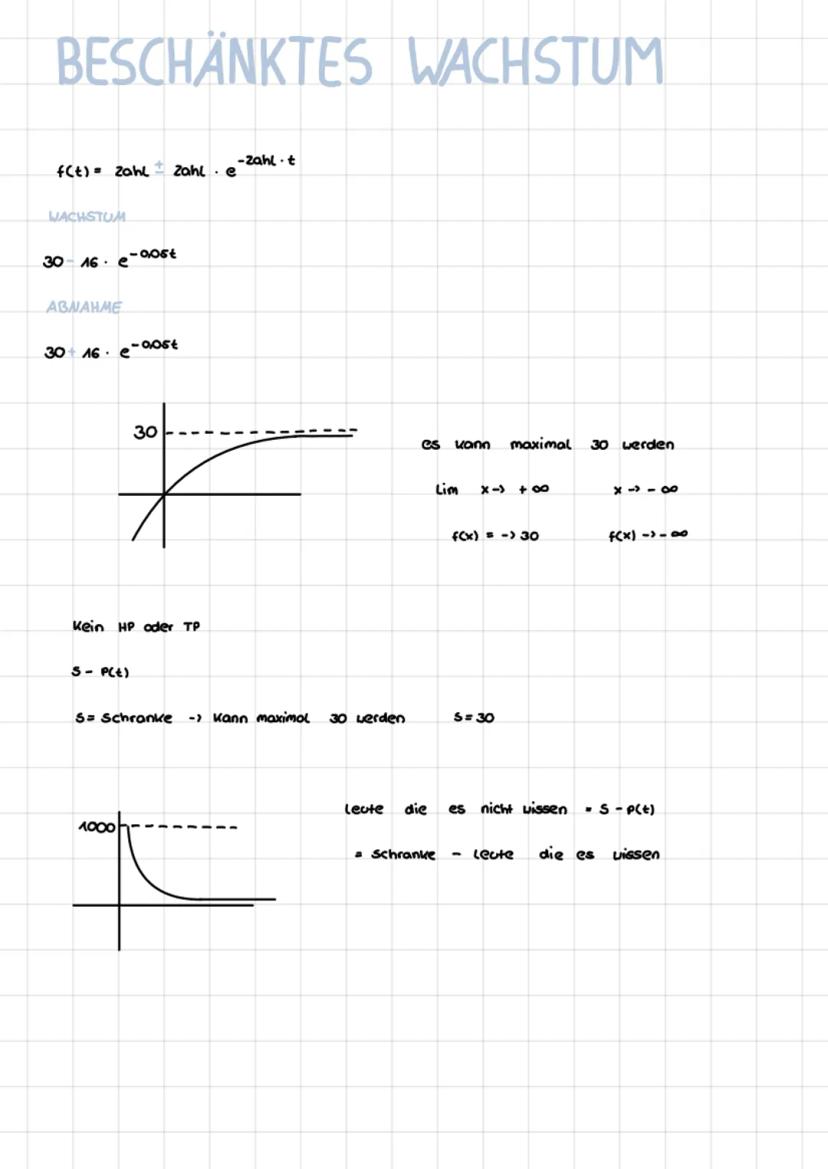
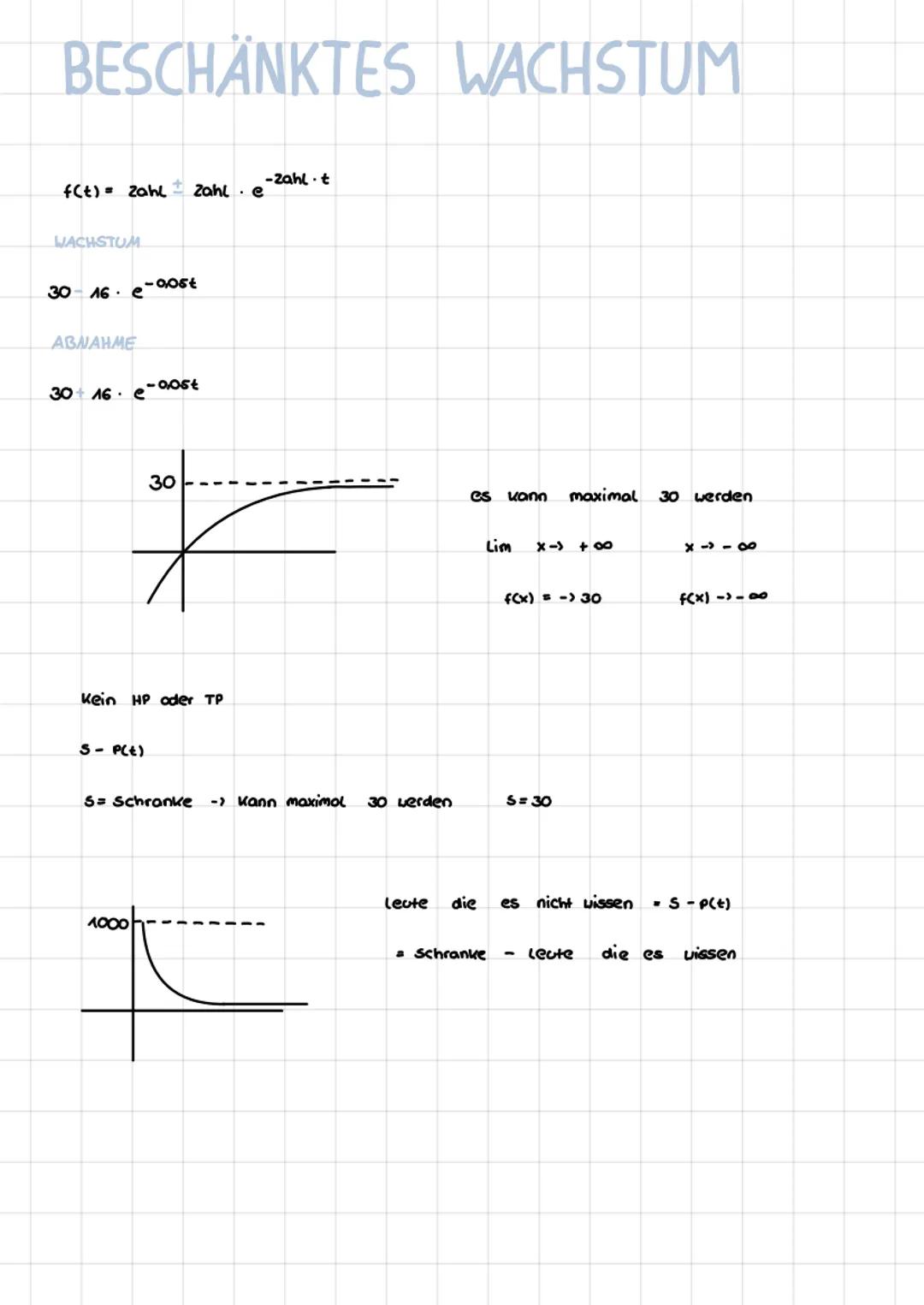
• Limited growth models are explored, showing how e-functions can model real-world phenomena.
• Advanced topics such as extrema, curvature analysis, and limit calculations are also covered.

11.5.2022

5364

E-FUNKTION
8888
f(x) = ex
f'(x) = ex
GRAPHISCH
all.
lex
e- gleichung
S = 3*
Log 35 = x
=> Log
1.log
streng monoton steigend
keine Nullstelle

Monotonicity and Tangent Lines

This page focuses on analyzing the monotonicity of e-functions and finding points where tangent lines have specific properties. The concept of using the first derivative to determine intervals of increasing and decreasing function values is explored in detail.

The process of finding points with horizontal tangent lines is demonstrated:

Set the first derivative equal to zero: f'(x) = 0
Solve the resulting equation to find x-values
These x-values correspond to points where the tangent line is horizontal

Example: For f(x) = x · e^x, setting f'(x) = e^x(1+x) = 0 leads to x = -1, which is the point with a horizontal tangent.

The page also covers how to determine intervals of increasing and decreasing function values using a sign chart of the first derivative.

Highlight: E-functions often have a single point where the tangent line is horizontal, which corresponds to the function's minimum point.

Vocabulary: Kettenregel e-Funktion Beispiel refers to examples demonstrating the application of the chain rule to e-functions.

Öffnen

Limited Growth Models

This page introduces the concept of beschränktes Wachstum (limited growth) and how e-functions can model such phenomena. The general form of a limited growth function is presented and analyzed.

Key features of limited growth models:

The function approaches a limiting value (asymptote) as time increases
The rate of growth decreases as the function approaches its limit
The model often takes the form f(t) = S - (S-P₀)e^(-kt), where S is the limiting value, P₀ is the initial value, and k is the growth rate

Definition: Beschränktes Wachstum refers to growth processes that have an upper limit or carrying capacity, often modeled using e-functions.

The page discusses how to analyze these models:

Identify the limiting value (S) and initial value (P₀)
Determine the growth rate (k) from given information
Analyze the long-term behavior as t approaches infinity

Example: A population model where the maximum population is 30 units, represented by f(t) = 30 - 16e^(-0.05t).

Highlight: Limited growth models are particularly useful in biology, economics, and other fields where resources or other factors impose upper limits on growth.

The page also covers how to interpret the parameters of the model and how changes in these parameters affect the behavior of the function.

Vocabulary: Beschränktes Wachstum Formel refers to the mathematical formula used to represent limited growth models.

Öffnen

Finding Zeros and Intersection Points

This page focuses on techniques for finding zeros and intersection points of e-functions, which are crucial skills for analyzing function behavior and solving equations involving e-functions.

The process of finding a zero for a function like f(x) = (3x-1) · e^-x is demonstrated:

Set the function equal to zero: (3x-1) · e^-x = 0
Since e^-x is never zero, solve 3x-1 = 0
The solution x = 1/3 is the zero of the function

Example: For f(x) = (3x-1) · e^-x, the zero is at x = 1/3.

The page also covers finding y-values for specific x-values and determining intersection points between e-functions and other functions.

Vocabulary: E-Funktion ableiten Rechner refers to calculators specifically designed to differentiate e-functions.

A method for finding intersection points is shown, which involves setting two functions equal to each other and solving the resulting equation, often requiring the use of logarithms.

Highlight: Finding intersection points between e-functions and linear functions often requires the use of logarithms to solve the resulting equations.

Öffnen

Extrema Problems and Optimization

This page focuses on applying e-functions to solve optimization problems, particularly finding maximum or minimum values in real-world scenarios. The concept of creating a target function and using calculus to find its extrema is explored.

Key steps in solving optimization problems:

Identify the quantity to be maximized or minimized
Express this quantity as a function of one variable (the target function)
Find the derivative of the target function
Set the derivative to zero and solve for the variable
Verify that the solution is indeed a maximum or minimum

Example: Maximizing the area of a rectangle with a given perimeter, where one side length is expressed as an e-function.

The page demonstrates how to set up the target function:

A = u · f(u), where A is the area, u is one side length, and f(u) is the other side length expressed as an e-function.

Highlight: Optimization problems involving e-functions often lead to solutions that balance exponential growth or decay with linear factors.

Vocabulary: Anwendungsaufgaben e-funktion Abitur refers to application problems involving e-functions that might appear in the Abitur (German high school exit exam).

Öffnen

Differentiation Rules for E-Functions

This page delves into the differentiation of e-functions, covering various rules and techniques. The basic rule for differentiating e^x is presented, showing that the derivative of e^x is itself.

Highlight: The unique property of e^x is that its derivative is equal to itself: f(x) = e^x, f'(x) = e^x.

The page then introduces more complex differentiation scenarios:

Kettenregel (Chain Rule): When dealing with functions like f(x) = e^(2x-1), the chain rule is applied.
Produktregel (Product Rule): For functions that are products involving e^x, such as f(x) = x · e^x, the product rule is used.

Example: Using the product rule to differentiate f(x) = (x-1) · e^x: f'(x) = (x-1) · e^x + 1 · e^x = (x) · e^x

The page provides several examples of combining these rules for more complex functions, demonstrating how to handle expressions involving both product and chain rules.

Vocabulary: Produktregel e-Funktion Rechner refers to calculators or tools designed to apply the product rule to e-functions.

Öffnen

E-Function Basics and Graphical Representation

This page introduces the fundamental concepts of the E-Funktion (exponential function) and its graphical properties. The e-function is defined as f(x) = e^x, with its derivative being f'(x) = e^x. The graph of the e-function is described as strictly monotonically increasing with no zeros.

Definition: The e-function, f(x) = e^x, is a fundamental exponential function in mathematics, where e is Euler's number (approximately 2.71828).

The page also discusses the behavior of the function as x approaches positive and negative infinity. As x approaches positive infinity, f(x) approaches positive infinity, and as x approaches negative infinity, f(x) approaches zero.

Highlight: The e-function has no zeros and is always positive, making it useful for modeling phenomena that never reach zero or negative values.

The natural logarithm (ln) is briefly mentioned as the inverse of the e-function, which is crucial for solving exponential equations.

Example: To solve an equation like 5 = e^x, we can take the natural logarithm of both sides: ln(5) = x.

Öffnen

Curvature Analysis

This page delves into the analysis of function curvature, focusing on the second derivative of e-functions. The concept of concavity and its relationship to the second derivative is explored in detail.

Key points covered include:

Using the second derivative to determine concavity
Finding inflection points where concavity changes
Analyzing the relationship between concavity and function behavior

Definition: Concavity refers to the curvature of a function's graph. A function is concave up when f''(x) > 0 and concave down when f''(x) < 0.

The page provides a step-by-step approach to curvature analysis:

Calculate the second derivative of the function
Determine intervals where f''(x) > 0 (concave up) and f''(x) < 0 (concave down)
Identify inflection points where f''(x) = 0 and concavity changes

Example: For a function f(t) = 0.04e^(-0.05t), the second derivative f''(t) = 0.04e^(-0.05t) is always positive, indicating the function is always concave up.

Highlight: E-functions often have a single inflection point where the concavity changes from concave up to concave down or vice versa.

The page also discusses the relationship between concavity and the function's rate of change, providing insights into how the shape of the graph relates to its mathematical properties.

Öffnen

Function Analysis: Extrema and Inflection Points

This page delves into the analysis of function behavior, focusing on identifying extrema and inflection points of e-functions. The concepts of first and second derivatives are utilized to determine these critical points.

Key points covered include:

Using the first derivative (f'(x)) to find potential extrema
Using the second derivative (f''(x)) to classify extrema and find inflection points
Identifying regions of increasing and decreasing function values

Definition: An inflection point is a point on a curve where the curvature changes sign, identified by f''(x) = 0 and a change in concavity.

The page provides a step-by-step approach to analyzing functions:

Find the first derivative and set it to zero to identify potential extrema
Use the second derivative to classify these points as maxima or minima
Identify inflection points where f''(x) = 0 and the concavity changes

Example: For f(x) = x · e^x, the extremum occurs at x = -1, which is a minimum point.

Highlight: The analysis of e-functions often reveals that they have no maximum points but may have a minimum and always have an inflection point.

Öffnen

Advanced Problem-Solving Techniques

This page covers advanced techniques for solving problems involving e-functions, including finding specific y-values, using the difference quotient, and calculating limits.

Key topics covered:

Solving equations involving e-functions for specific y-values
Calculating and interpreting the difference quotient
Evaluating limits of e-functions as t approaches infinity

Example: Solving for t in the equation A = 0.02 + 15e^(-0.4t) to find when a specific value of A is reached.

The page demonstrates how to use logarithms to solve exponential equations:

Isolate the exponential term
Take the natural logarithm of both sides
Solve for the variable

Highlight: The difference quotient is a key concept in calculus, representing the average rate of change of a function over an interval.

The page also covers limit calculations, particularly for e-functions as the variable approaches infinity. These limits are crucial for understanding the long-term behavior of exponential models.

Vocabulary: E-Funktionen ableiten Übungen refers to exercises focused on differentiating e-functions.

Öffnen

Integration of E-Functions

This page covers techniques for integrating e-functions, including definite and improper integrals. The fundamental property that the integral of e^x is e^x + C is emphasized and applied to more complex scenarios.

Key topics covered:

Basic integration of e^x
Integration by substitution for more complex e-functions
Definite integrals with finite limits
Improper integrals with infinite limits

Definition: An improper integral is an integral where one or both limits of integration are infinite, or the integrand has a vertical asymptote within the interval.

The page provides examples of solving improper integrals:

Set up the integral with a variable upper or lower limit
Evaluate the indefinite integral
Take the limit as the variable approaches infinity

Example: Evaluating ∫[0 to ∞] 4xe^x dx using the limit definition of an improper integral.

Highlight: When integrating e-functions over infinite intervals, the exponential growth often dominates, leading to divergent integrals unless there are counterbalancing factors.

The page also discusses techniques for determining whether an improper integral converges or diverges, which is crucial for understanding the total area under e-function curves over infinite intervals.

Nichts passendes dabei? Erkunde andere Fachbereiche.

Knowunity ist die #1 unter den Bildungs-Apps in fünf europäischen Ländern

Knowunity wurde bei Apple als "Featured Story" ausgezeichnet und hat die App-Store-Charts in der Kategorie Bildung in Deutschland, Italien, Polen, der Schweiz und dem Vereinigten Königreich regelmäßig angeführt. Werde noch heute Mitglied bei Knowunity und hilf Millionen von Schüler:innen auf der ganzen Welt.

Laden im

Google Play

Laden im

App Store

Knowunity ist die #1 unter den Bildungs-Apps in fünf europäischen Ländern

4.9+

Durchschnittliche App-Bewertung

13 M

Schüler:innen lieben Knowunity

#1

In Bildungs-App-Charts in 12 Ländern

950 K+

Schüler:innen haben Lernzettel hochgeladen

Immer noch nicht überzeugt? Schau dir an, was andere Schüler:innen sagen...

iOS User

Ich liebe diese App so sehr, ich benutze sie auch täglich. Ich empfehle Knowunity jedem!! Ich bin damit von einer 4 auf eine 1 gekommen :D

Philipp, iOS User

Die App ist sehr einfach und gut gestaltet. Bis jetzt habe ich immer alles gefunden, was ich gesucht habe :D

Lena, iOS Userin

Ich liebe diese App ❤️, ich benutze sie eigentlich immer, wenn ich lerne.

Nichts passendes dabei? Erkunde andere Fachbereiche.

Knowunity ist die #1 unter den Bildungs-Apps in fünf europäischen Ländern

Knowunity wurde bei Apple als "Featured Story" ausgezeichnet und hat die App-Store-Charts in der Kategorie Bildung in Deutschland, Italien, Polen, der Schweiz und dem Vereinigten Königreich regelmäßig angeführt. Werde noch heute Mitglied bei Knowunity und hilf Millionen von Schüler:innen auf der ganzen Welt.

Laden im

Google Play

Laden im

App Store

4.9+

Durchschnittliche App-Bewertung

13 M

Schüler:innen lieben Knowunity

#1

In Bildungs-App-Charts in 12 Ländern

950 K+

Schüler:innen haben Lernzettel hochgeladen

Immer noch nicht überzeugt? Schau dir an, was andere Schüler:innen sagen...

iOS User

Ich liebe diese App so sehr, ich benutze sie auch täglich. Ich empfehle Knowunity jedem!! Ich bin damit von einer 4 auf eine 1 gekommen :D

Philipp, iOS User

Die App ist sehr einfach und gut gestaltet. Bis jetzt habe ich immer alles gefunden, was ich gesucht habe :D

Lena, iOS Userin

Ich liebe diese App ❤️, ich benutze sie eigentlich immer, wenn ich lerne.

Fächer

Mathe

Funktionen und analysis

Kurvendiskussion einzelschritte

Grenzwert

E-Funktion einfach erklärt: Ableitungsrechner, Produktregel & Kettenregel

Carina

@carina_sophie

30 Follower

11.5.2022

5364

11/12

Mathe

129

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Monotonicity and Tangent Lines

The process of finding points with horizontal tangent lines is demonstrated:

Set the first derivative equal to zero: f'(x) = 0
Solve the resulting equation to find x-values
These x-values correspond to points where the tangent line is horizontal

Example: For f(x) = x · e^x, setting f'(x) = e^x(1+x) = 0 leads to x = -1, which is the point with a horizontal tangent.

The page also covers how to determine intervals of increasing and decreasing function values using a sign chart of the first derivative.

Highlight: E-functions often have a single point where the tangent line is horizontal, which corresponds to the function's minimum point.

Vocabulary: Kettenregel e-Funktion Beispiel refers to examples demonstrating the application of the chain rule to e-functions.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Limited Growth Models

This page introduces the concept of beschränktes Wachstum (limited growth) and how e-functions can model such phenomena. The general form of a limited growth function is presented and analyzed.

Key features of limited growth models:

The function approaches a limiting value (asymptote) as time increases
The rate of growth decreases as the function approaches its limit
The model often takes the form f(t) = S - (S-P₀)e^(-kt), where S is the limiting value, P₀ is the initial value, and k is the growth rate

Definition: Beschränktes Wachstum refers to growth processes that have an upper limit or carrying capacity, often modeled using e-functions.

The page discusses how to analyze these models:

Identify the limiting value (S) and initial value (P₀)
Determine the growth rate (k) from given information
Analyze the long-term behavior as t approaches infinity

Example: A population model where the maximum population is 30 units, represented by f(t) = 30 - 16e^(-0.05t).

Highlight: Limited growth models are particularly useful in biology, economics, and other fields where resources or other factors impose upper limits on growth.

The page also covers how to interpret the parameters of the model and how changes in these parameters affect the behavior of the function.

Vocabulary: Beschränktes Wachstum Formel refers to the mathematical formula used to represent limited growth models.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Finding Zeros and Intersection Points

This page focuses on techniques for finding zeros and intersection points of e-functions, which are crucial skills for analyzing function behavior and solving equations involving e-functions.

The process of finding a zero for a function like f(x) = (3x-1) · e^-x is demonstrated:

Set the function equal to zero: (3x-1) · e^-x = 0
Since e^-x is never zero, solve 3x-1 = 0
The solution x = 1/3 is the zero of the function

Example: For f(x) = (3x-1) · e^-x, the zero is at x = 1/3.

The page also covers finding y-values for specific x-values and determining intersection points between e-functions and other functions.

Vocabulary: E-Funktion ableiten Rechner refers to calculators specifically designed to differentiate e-functions.

A method for finding intersection points is shown, which involves setting two functions equal to each other and solving the resulting equation, often requiring the use of logarithms.

Highlight: Finding intersection points between e-functions and linear functions often requires the use of logarithms to solve the resulting equations.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Extrema Problems and Optimization

Key steps in solving optimization problems:

Identify the quantity to be maximized or minimized
Express this quantity as a function of one variable (the target function)
Find the derivative of the target function
Set the derivative to zero and solve for the variable
Verify that the solution is indeed a maximum or minimum

Example: Maximizing the area of a rectangle with a given perimeter, where one side length is expressed as an e-function.

The page demonstrates how to set up the target function:

A = u · f(u), where A is the area, u is one side length, and f(u) is the other side length expressed as an e-function.

Highlight: Optimization problems involving e-functions often lead to solutions that balance exponential growth or decay with linear factors.

Vocabulary: Anwendungsaufgaben e-funktion Abitur refers to application problems involving e-functions that might appear in the Abitur (German high school exit exam).

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Differentiation Rules for E-Functions

This page delves into the differentiation of e-functions, covering various rules and techniques. The basic rule for differentiating e^x is presented, showing that the derivative of e^x is itself.

Highlight: The unique property of e^x is that its derivative is equal to itself: f(x) = e^x, f'(x) = e^x.

The page then introduces more complex differentiation scenarios:

Kettenregel (Chain Rule): When dealing with functions like f(x) = e^(2x-1), the chain rule is applied.
Produktregel (Product Rule): For functions that are products involving e^x, such as f(x) = x · e^x, the product rule is used.

Example: Using the product rule to differentiate f(x) = (x-1) · e^x: f'(x) = (x-1) · e^x + 1 · e^x = (x) · e^x

The page provides several examples of combining these rules for more complex functions, demonstrating how to handle expressions involving both product and chain rules.

Vocabulary: Produktregel e-Funktion Rechner refers to calculators or tools designed to apply the product rule to e-functions.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

E-Function Basics and Graphical Representation

Definition: The e-function, f(x) = e^x, is a fundamental exponential function in mathematics, where e is Euler's number (approximately 2.71828).

Highlight: The e-function has no zeros and is always positive, making it useful for modeling phenomena that never reach zero or negative values.

The natural logarithm (ln) is briefly mentioned as the inverse of the e-function, which is crucial for solving exponential equations.

Example: To solve an equation like 5 = e^x, we can take the natural logarithm of both sides: ln(5) = x.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Curvature Analysis

Key points covered include:

Using the second derivative to determine concavity
Finding inflection points where concavity changes
Analyzing the relationship between concavity and function behavior

Definition: Concavity refers to the curvature of a function's graph. A function is concave up when f''(x) > 0 and concave down when f''(x) < 0.

The page provides a step-by-step approach to curvature analysis:

Calculate the second derivative of the function
Determine intervals where f''(x) > 0 (concave up) and f''(x) < 0 (concave down)
Identify inflection points where f''(x) = 0 and concavity changes

Example: For a function f(t) = 0.04e^(-0.05t), the second derivative f''(t) = 0.04e^(-0.05t) is always positive, indicating the function is always concave up.

Highlight: E-functions often have a single inflection point where the concavity changes from concave up to concave down or vice versa.

The page also discusses the relationship between concavity and the function's rate of change, providing insights into how the shape of the graph relates to its mathematical properties.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Function Analysis: Extrema and Inflection Points

Key points covered include:

Using the first derivative (f'(x)) to find potential extrema
Using the second derivative (f''(x)) to classify extrema and find inflection points
Identifying regions of increasing and decreasing function values

Definition: An inflection point is a point on a curve where the curvature changes sign, identified by f''(x) = 0 and a change in concavity.

The page provides a step-by-step approach to analyzing functions:

Find the first derivative and set it to zero to identify potential extrema
Use the second derivative to classify these points as maxima or minima
Identify inflection points where f''(x) = 0 and the concavity changes

Example: For f(x) = x · e^x, the extremum occurs at x = -1, which is a minimum point.

Highlight: The analysis of e-functions often reveals that they have no maximum points but may have a minimum and always have an inflection point.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Advanced Problem-Solving Techniques

This page covers advanced techniques for solving problems involving e-functions, including finding specific y-values, using the difference quotient, and calculating limits.

Key topics covered:

Solving equations involving e-functions for specific y-values
Calculating and interpreting the difference quotient
Evaluating limits of e-functions as t approaches infinity

Example: Solving for t in the equation A = 0.02 + 15e^(-0.4t) to find when a specific value of A is reached.

The page demonstrates how to use logarithms to solve exponential equations:

Isolate the exponential term
Take the natural logarithm of both sides
Solve for the variable

Highlight: The difference quotient is a key concept in calculus, representing the average rate of change of a function over an interval.

The page also covers limit calculations, particularly for e-functions as the variable approaches infinity. These limits are crucial for understanding the long-term behavior of exponential models.

Vocabulary: E-Funktionen ableiten Übungen refers to exercises focused on differentiating e-functions.

Melde dich an, um den Inhalt freizuschalten. Es ist kostenlos!

Zugriff auf alle Dokumente

Werde Teil der Community

Verbessere deine Noten

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Integration of E-Functions

Key topics covered:

Basic integration of e^x
Integration by substitution for more complex e-functions
Definite integrals with finite limits
Improper integrals with infinite limits

Definition: An improper integral is an integral where one or both limits of integration are infinite, or the integrand has a vertical asymptote within the interval.

The page provides examples of solving improper integrals:

Set up the integral with a variable upper or lower limit
Evaluate the indefinite integral
Take the limit as the variable approaches infinity

Example: Evaluating ∫[0 to ∞] 4xe^x dx using the limit definition of an improper integral.

Highlight: When integrating e-functions over infinite intervals, the exponential growth often dominates, leading to divergent integrals unless there are counterbalancing factors.