Lineare Funktionen verstehen
Lineare Funktionen sind eigentlich ziemlich einfach: Sie ordnen jeder x-Zahl genau einen y-Wert zu. Das Besondere daran? Ihr Graph ist immer eine gerade Linie - daher auch der Name "linear"!
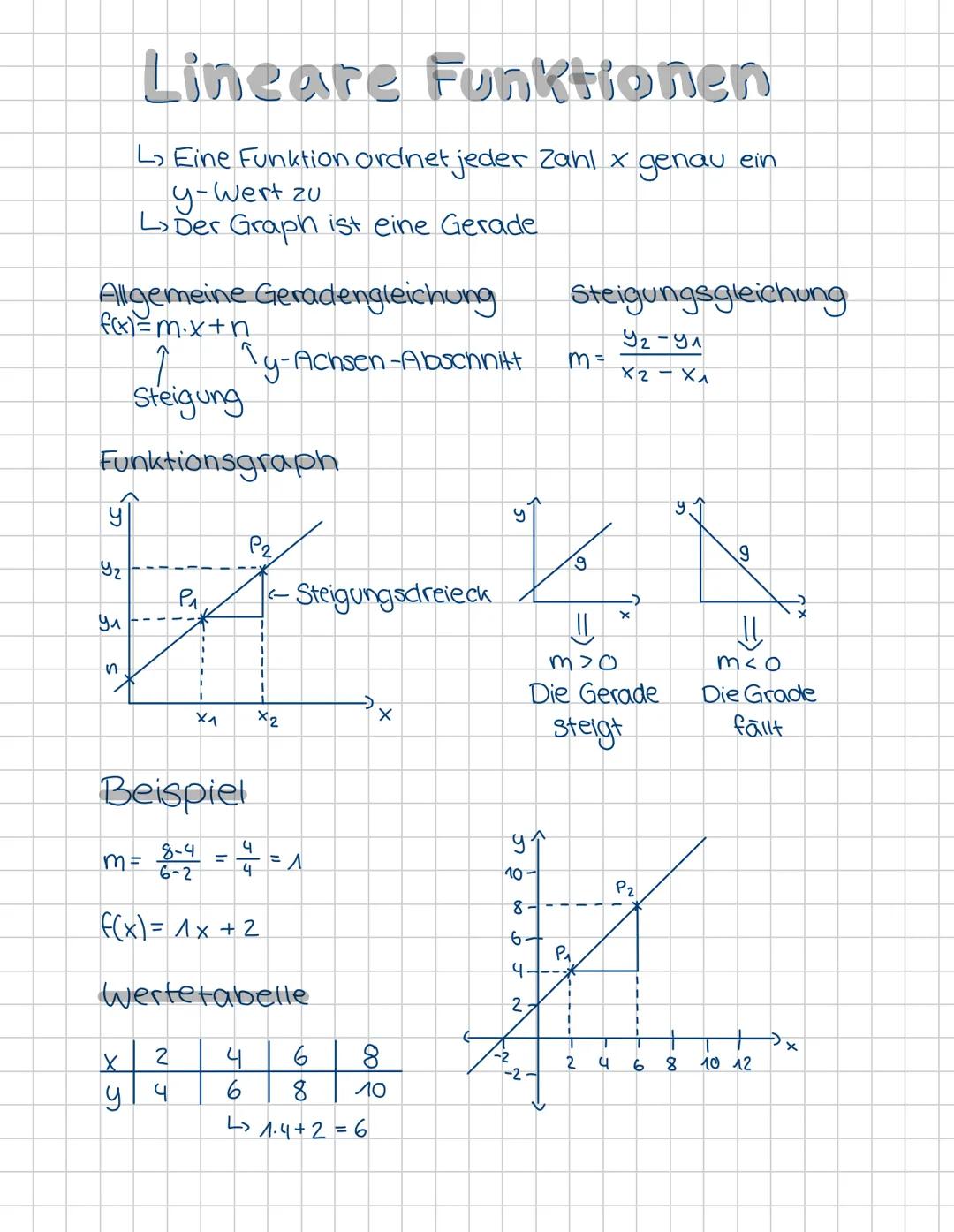
Die allgemeine Geradengleichung lautet: f(x) = m·x + n. Hier ist "m" die Steigung und "n" der y-Achsen-Abschnitt. Der y-Achsen-Abschnitt zeigt dir, wo die Gerade die y-Achse schneidet.
Die Steigung berechnest du mit der Formel: m = y2−y1/x2−x1. Du brauchst dafür einfach zwei Punkte auf der Geraden. Ist m > 0, dann steigt die Gerade. Ist m < 0, dann fällt sie.
Merktipp: Das Steigungsdreieck hilft dir dabei, die Steigung abzulesen - einfach "hoch durch rechts"!
Im Beispiel mit den Punkten (2,4) und (6,8) rechnest du: m = (8-4)/(6-2) = 4/4 = 1. Die komplette Funktion ist dann f(x) = 1·x + 2.