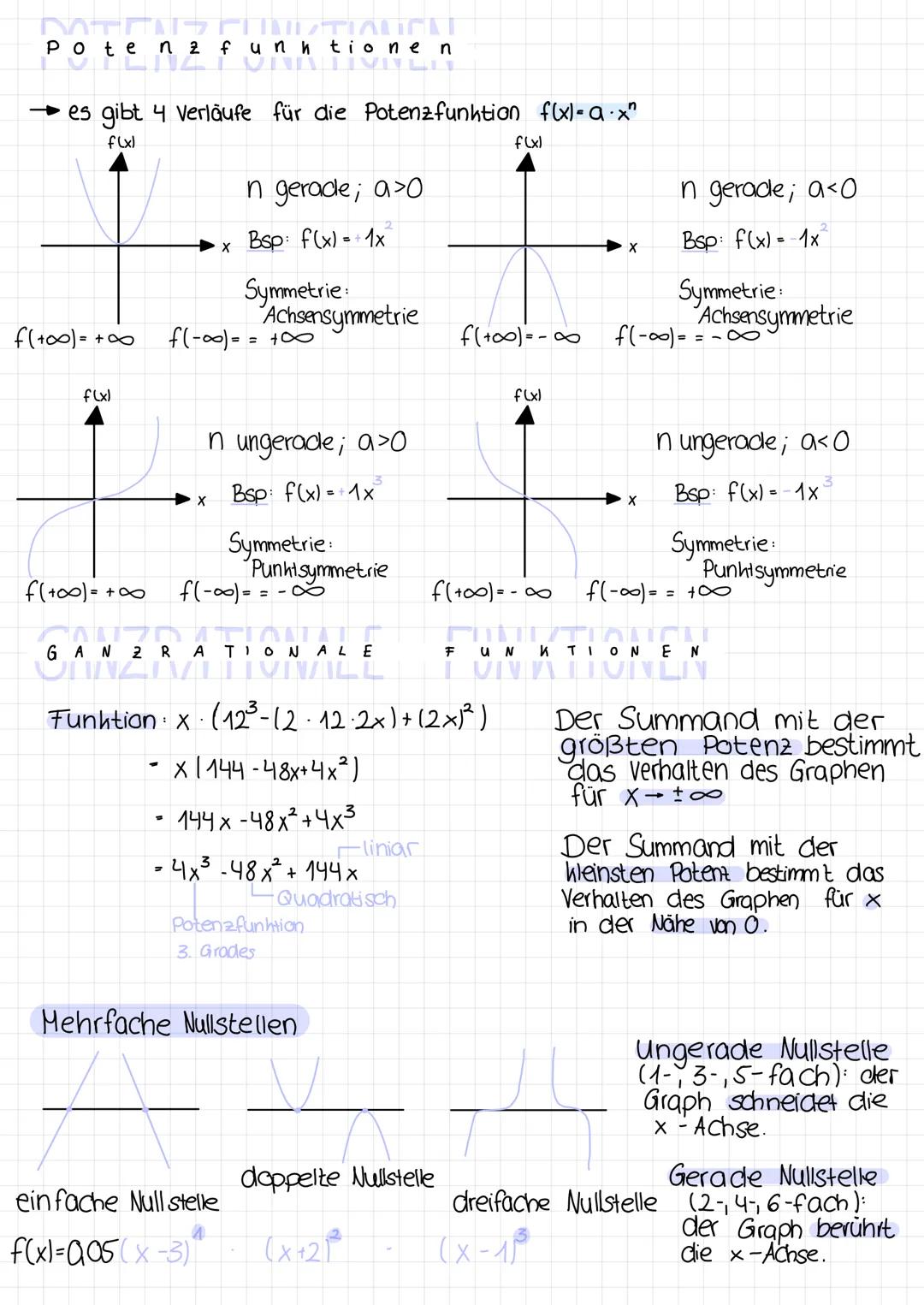
Es gibt 4 Verläufe für die Potenzfunktion f(x)=a*x^n:
- Gerader Exponent (n gerade; a>0)
- Beispiel: f(x) = 1 * x²
- Symmetrie: Achsensymmetrie
- Verhalten: f(x) für x → +∞ = +∞ und f(x) für x → -∞ = +∞
- Ungerader Exponent (n ungerade; a>0)
- Beispiel: f(x) = 1 * x
- Symmetrie: Punktsymmetrie
- Verhalten: f(x) für x → +∞ = +∞ und f(x) für x → -∞ = -∞
- Gerader Exponent (n gerade; a<0)
- Beispiel: f(x) = -1 * x²
- Symmetrie: Achsensymmetrie
- Verhalten: f(x) für x → +∞ = -∞ und f(x) für x → -∞ = +∞
- Ungerader Exponent (n ungerade; a<0)
- Beispiel: f(x) = -1 * x
- Symmetrie: Punktsymmetrie
- Verhalten: f(x) für x → +∞ = -∞ und f(x) für x → -∞ = -∞
Die Summanden mit der größten bzw. kleinste Potenz bestimmen das Verhalten des Graphen für x → +∞ bzw. in der Nähe von 0.
Nullstellen bei ganzrationalen Funktionen
Ablesen von Nullstellen
Bei ganzrationalen Funktionen kann man die Nullstellen durch Ablesen bestimmen oder durch Ausklammern der Variablen. Falls die Funktion nur aus Liniarfaktoren besteht, können die Nullstellen durch den Nullproduktsatz bestimmt werden. Immer sollten die Nullstellen angegeben werden.
Ausklammern und Substitution
Falls die Funktionsgleichung nur aus Summanden mit Variablen (x) besteht, kann man die Nullstellen durch Ausklammern oder durch Substitution bestimmen.
In einer Klausur ist es wichtig, Nullstellen korrekt zu bestimmen und anzugeben.
Symmetrien und Transformationen
Die Symmetrie einer Funktion kann durch die Eigenschaften der Exponenten bestimmt werden. Alle Exponenten gerade bedeuten Achsensymmetrie, während alle Exponenten ungerade Punktsymmetrie bedeuten.
Für die Transformationen von Funktionen gelten bestimmte Regeln für Verschiebungen in x- und y-Richtung sowie für Streckungen und Stauchungen.
Bei der Zeichnung von Graphen ist es wichtig, die Transformationen zu berücksichtigen und den Graphen entsprechend zu zeichnen.
Zusammenfassung
Potenzfunktionen 3. Grades und ganzrationale Funktionen lassen sich anhand ihrer Symmetrien, Nullstellen und Transformationsregeln erkennen. Es ist wichtig, die verschiedenen Verläufe und Eigenschaften zu verstehen, um die Graphen korrekt zeichnen und die Funktionen angemessen analysieren zu können. Übungen zur Bestimmung von Nullstellen und zur Zeichnung von Graphen sind essentiell, um das Verständnis für ganzrationale Funktionen zu vertiefen.