Analysis - Funktionen verstehen
Funktionen sind das Herzstück der Analysis - jeder x-Wert hat genau einen y-Wert, sonst wäre es nur eine Relation. Du schreibst sie als f(x)=8x2−4 und jeder Punkt hat die Form (x∣f(x)).
Schnittpunkte findest du so: Für die y-Achse setzt du x=0 ein, für Nullstellen x−Achse machst du f(x)=0 und löst nach x auf. Bei quadratischen Funktionen helfen dir die pq-Formel $x_{1,2} = -\frac{p}{2} \pm \sqrt{(\frac{p}{2})^2 - q}$ oder abc-Formel.
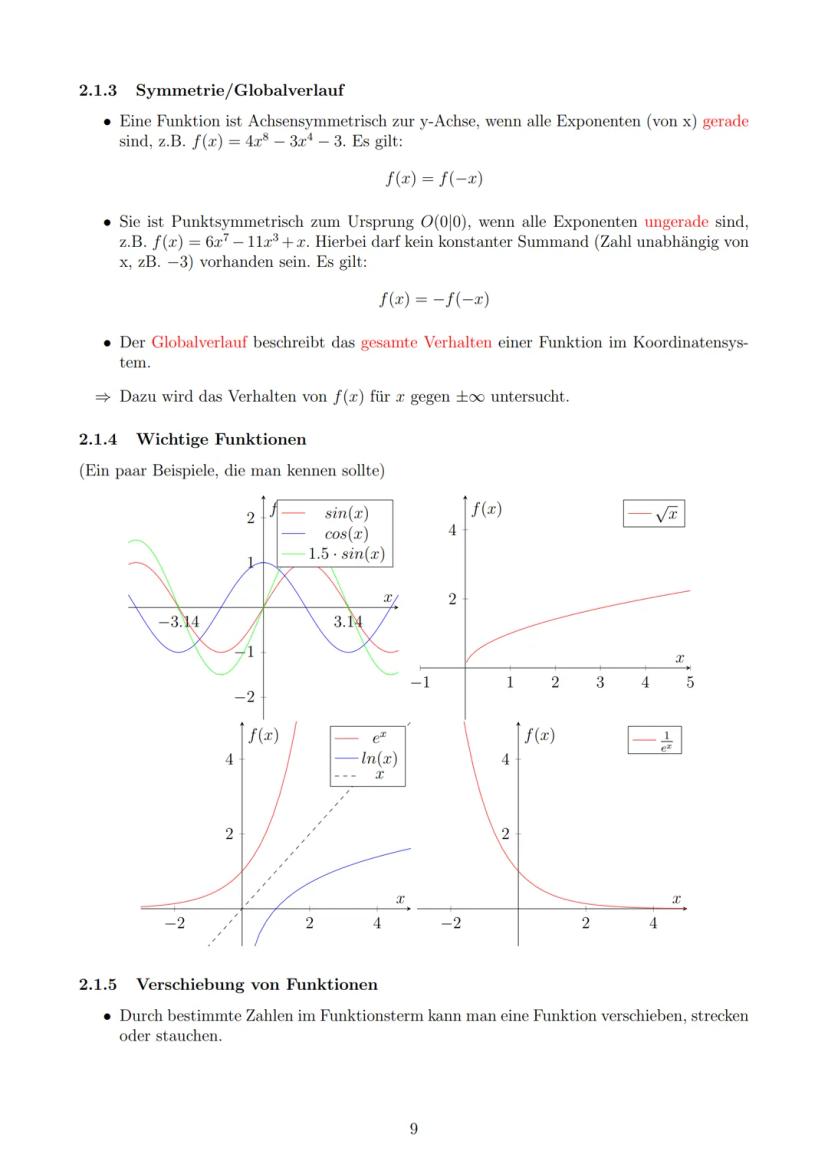
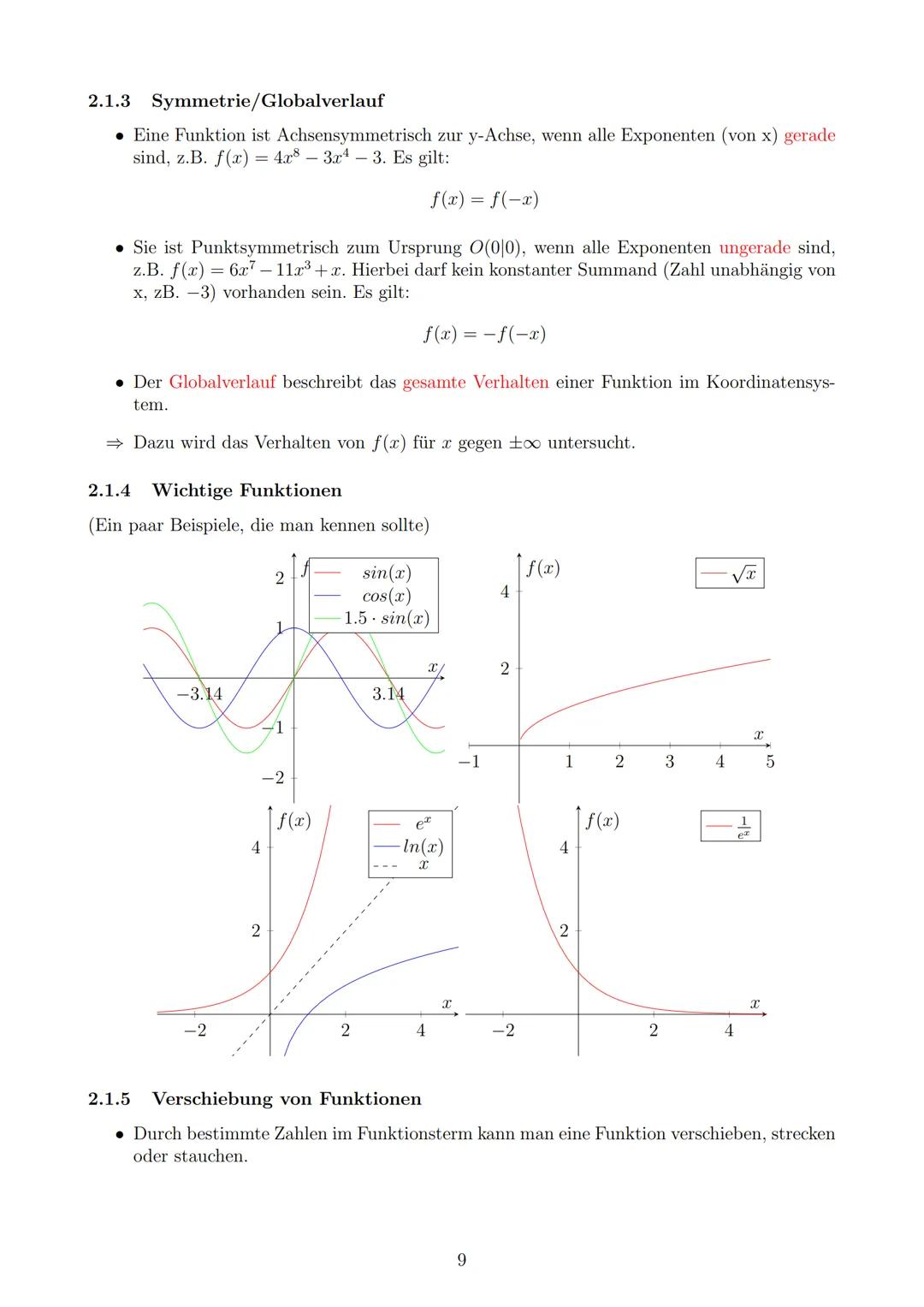
Symmetrie erkennst du an den Exponenten: Alle gerade = achsensymmetrisch zur y-Achse $f(x) = f(-x)$, alle ungerade = punktsymmetrisch zum Ursprung $f(x) = -f(-x)$. Der Globalverlauf zeigt dir, wie sich die Funktion für sehr große und sehr kleine x-Werte verhält.
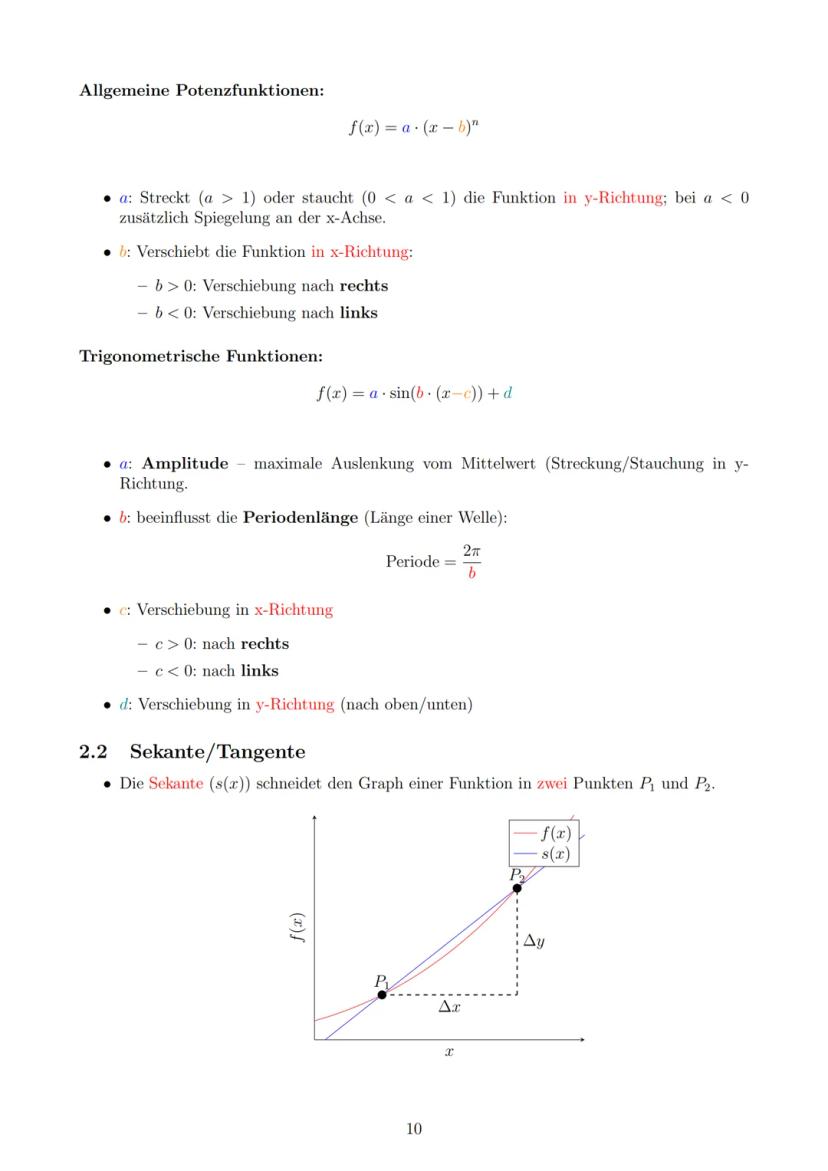
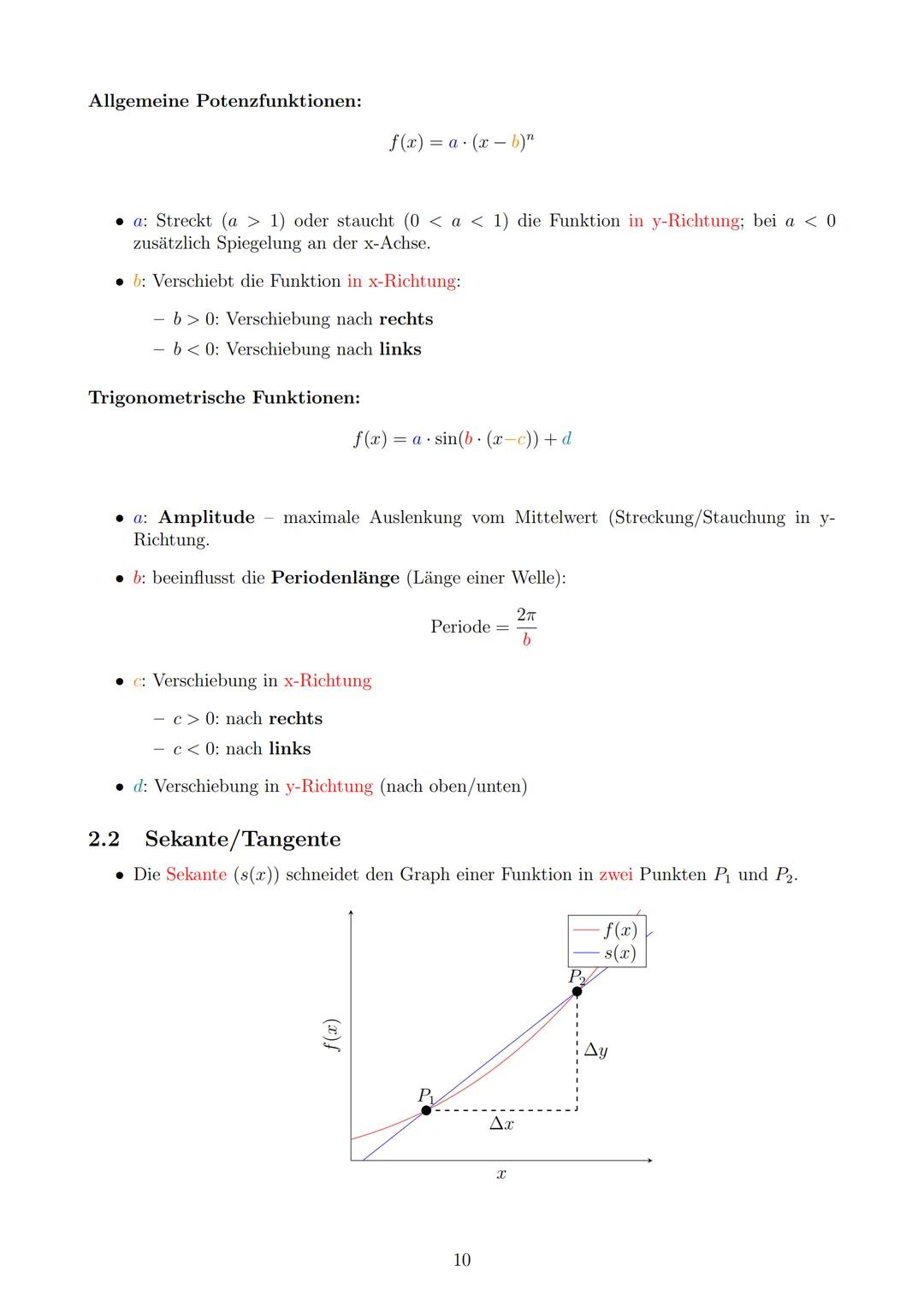
Bei Funktionsverschiebungen gilt: a streckt/staucht in y-Richtung, b verschiebt in x-Richtung. Bei Sinus und Cosinus bestimmt die Amplitude die Höhe, die Periode die Wellenlänge.
Eselsbrücke: Bei (x−b)n geht's andersrum - plus b bedeutet Verschiebung nach rechts, nicht links!