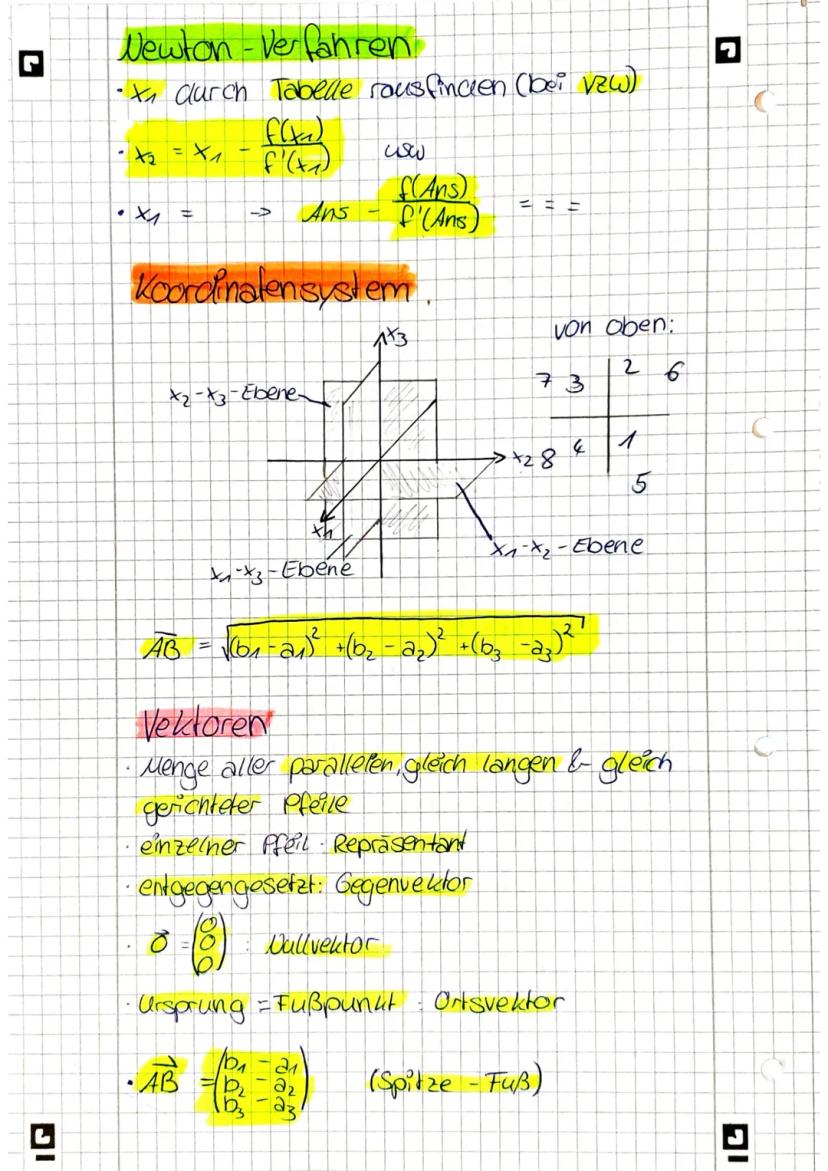
Zusammenfassung der Themen der Mathe Klausur in Q11/1
Melde dich an, um den Inhalt freizuschaltenEs ist kostenlos!
Zugriff auf alle Dokumente
Verbessere deine Noten
Werde Teil der Community
Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie