Grundlagen der Vektoren

Vektoren sind super praktisch, um Bewegungen im 3D-Raum zu beschreiben. Stell dir vor, du willst jemandem erklären, wie er von einem Punkt zum anderen kommt - genau das machen Vektoren!

Ein Vektor ist eine Klasse von Pfeilen, die alle die gleiche Länge, Richtung und Orientierung haben. Im Gegensatz zu Punkten haben sie keine feste Position im Raum. Du kannst sie dir wie Verschiebungsanweisungen vorstellen.

Punkte im Raum werden mit drei Koordinaten beschrieben: P(x₁|x₂|x₃). Die x₁x₂-Ebene entsteht durch die ersten beiden Koordinaten und erstreckt sich unbegrenzt in alle Richtungen.

Tipp: Denk an Vektoren wie an GPS-Anweisungen - sie sagen dir, in welche Richtung und wie weit du gehen musst, aber nicht wo du startest!

Wichtige Vektorarten und Geradengleichungen

Der Ortsvektor eines Punktes A zeigt immer vom Ursprung zu diesem Punkt: OA⃗. Der Nullvektor ist besonders: Er hat keine Länge und keine Richtung - mathematisch gesehen gibt es zu ihm keinen Pfeil.

Linearkombinationen entstehen, wenn du Vektoren mit Zahlen multiplizierst und dann addierst. Das ist wie beim Mischen von Farben - du bekommst neue "Vektorfarben".

Für Geradengleichungen brauchst du zwei Dinge: einen Stützpunkt (wo die Gerade durchgeht) und einen Richtungsvektor (in welche Richtung sie verläuft). Die Formel lautet: g: x⃗ = p⃗ + t·u⃗.

Merkhilfe: Stützvektor + Parameter × Richtungsvektor = jeder Punkt auf der Geraden. Der Parameter t kann jeden reellen Wert annehmen!

Lösungsmengen linearer Gleichungssysteme

Lineare Gleichungssysteme können drei verschiedene Arten von Lösungen haben. Das ist wichtig für deine Klassenarbeiten!

Eine eindeutige Lösung bekommst du, wenn sich alle Gleichungen in genau einem Punkt treffen. Beispiel: L = {(6; 2; 3)} - es gibt nur diese eine Lösung.

Keine Lösung bedeutet, dass die Gleichungen sich widersprechen. Wenn du auf etwas wie "0 = -2" stößt, ist das mathematisch unmöglich - die Lösungsmenge ist leer: L = {}.

Unendlich viele Lösungen entstehen, wenn eine Gleichung überflüssig wird $wie "0 = 0"$. Dann bekommst du eine Lösungsmenge mit einem Parameter: L = {$5 + 4,5t; 2 + 2t; t$; t ∈ ℝ}.

Prüfungstrick: Arbeite systematisch von unten nach oben - löse zuerst die einfachste Gleichung und setze dann nach oben ein!

Lagebeziehungen von Geraden

Zwei Geraden können sich auf verschiedene Weise zueinander verhalten. Das musst du systematisch prüfen können!

Schritt 1: Prüfe die Richtungsvektoren. Sind sie Vielfache voneinander? Dann sind die Geraden parallel oder identisch. Mit einer Punktprobe findest du heraus, welcher Fall vorliegt.

Schritt 2: Sind die Richtungsvektoren keine Vielfachen? Dann setze die Geradengleichungen gleich und löse das Gleichungssystem. Gibt es eine Lösung, haben die Geraden einen Schnittpunkt. Gibt es keine Lösung, sind sie windschief (kreuzen sich im Raum, ohne sich zu berühren).

Für Ebenengleichungen brauchst du einen Stützpunkt und zwei linear unabhängige Spannvektoren: E: x⃗ = p⃗ + r·u⃗ + s·v⃗. Die Spannvektoren dürfen nicht parallel sein!

Eselsbrücke: Parallel = gleiche Richtung, windschief = aneinander vorbei im Raum, Schnittpunkt = treffen sich genau einmal!

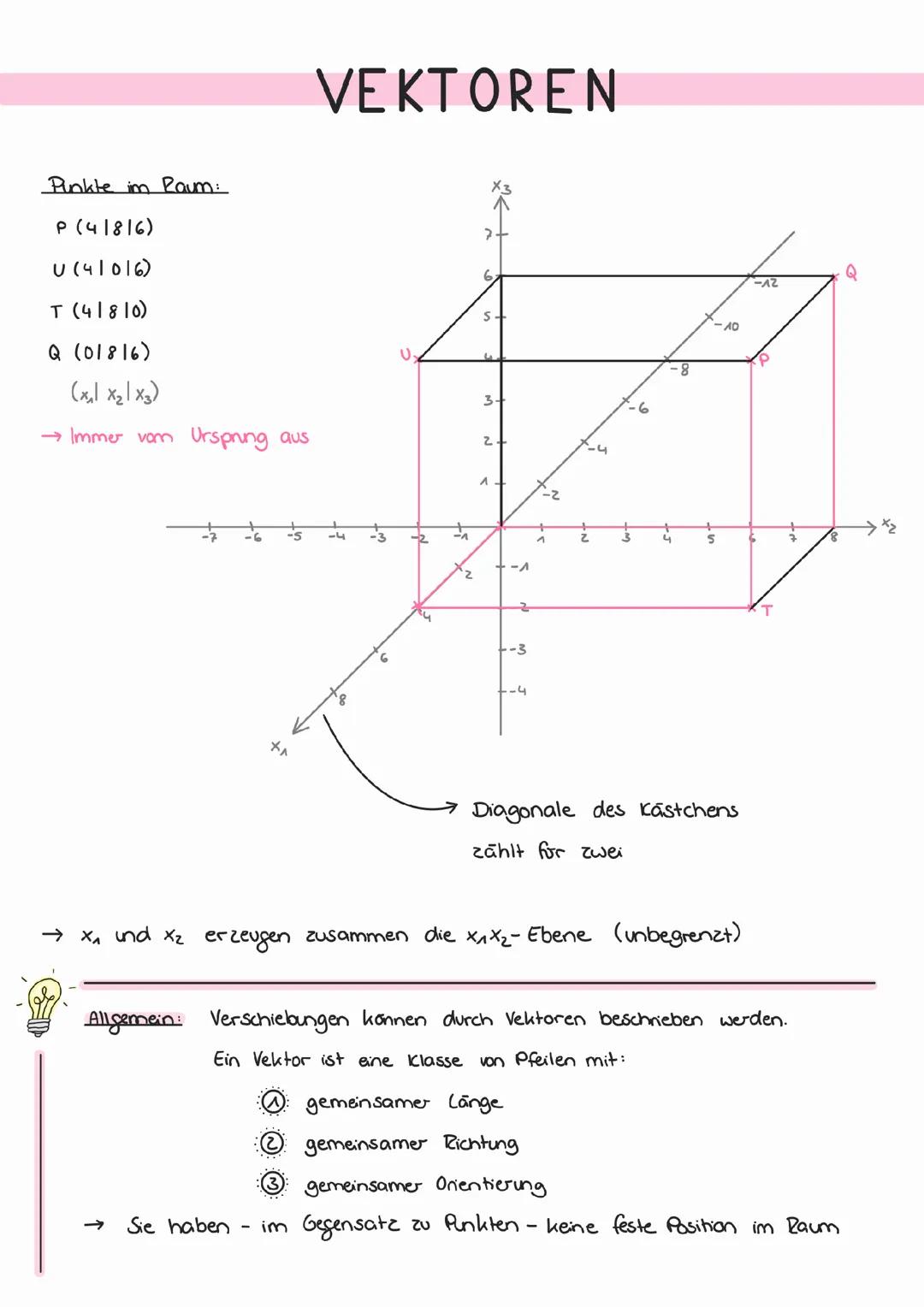
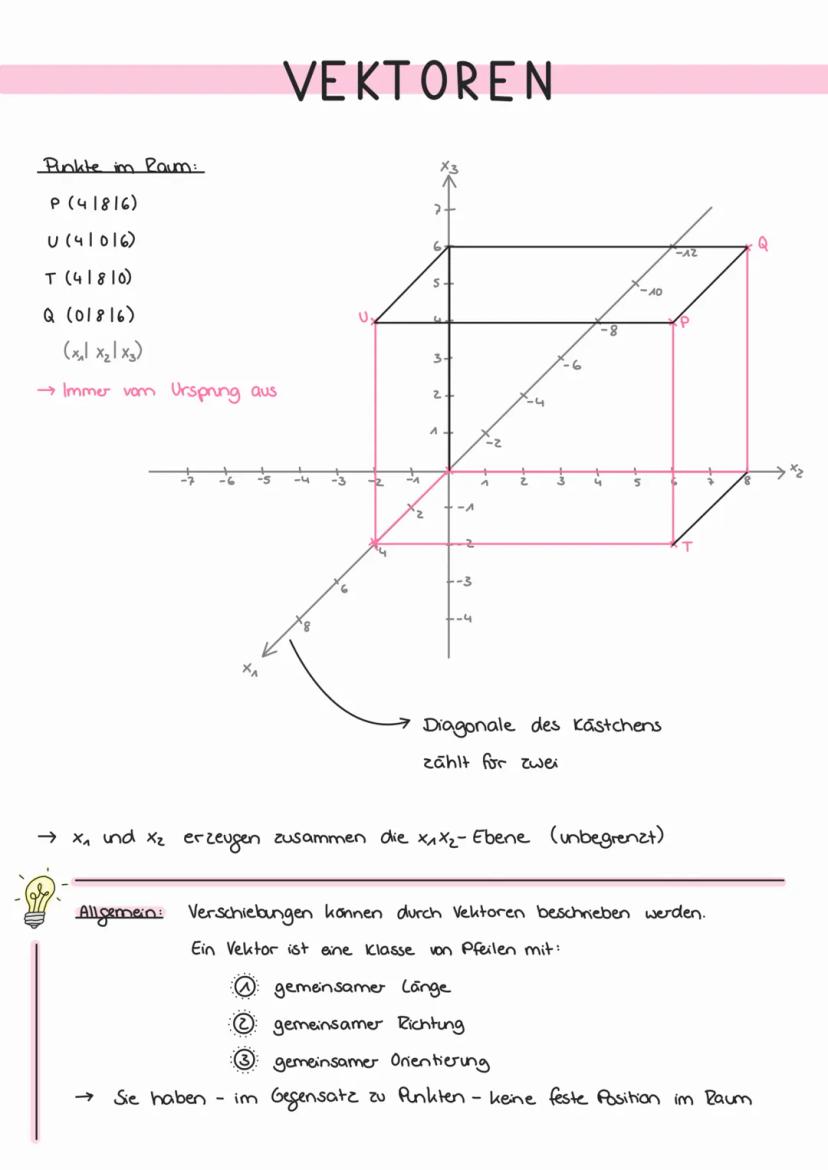
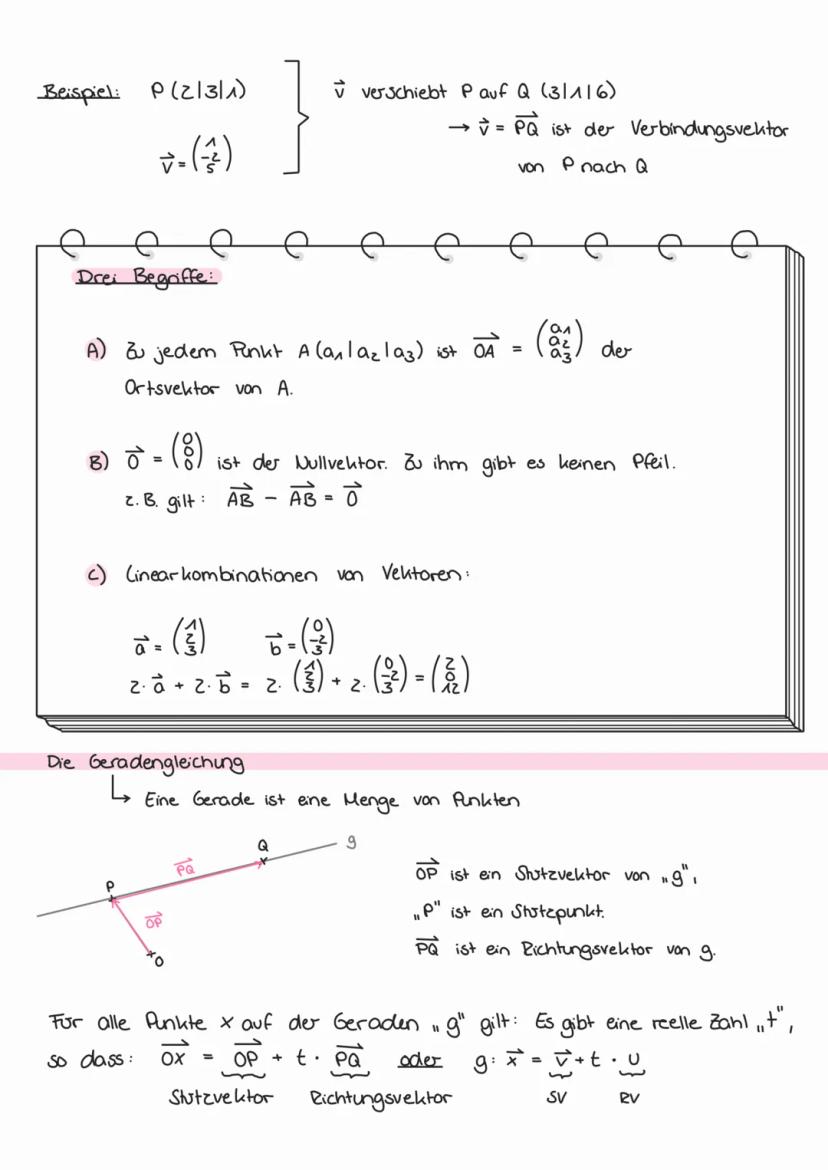
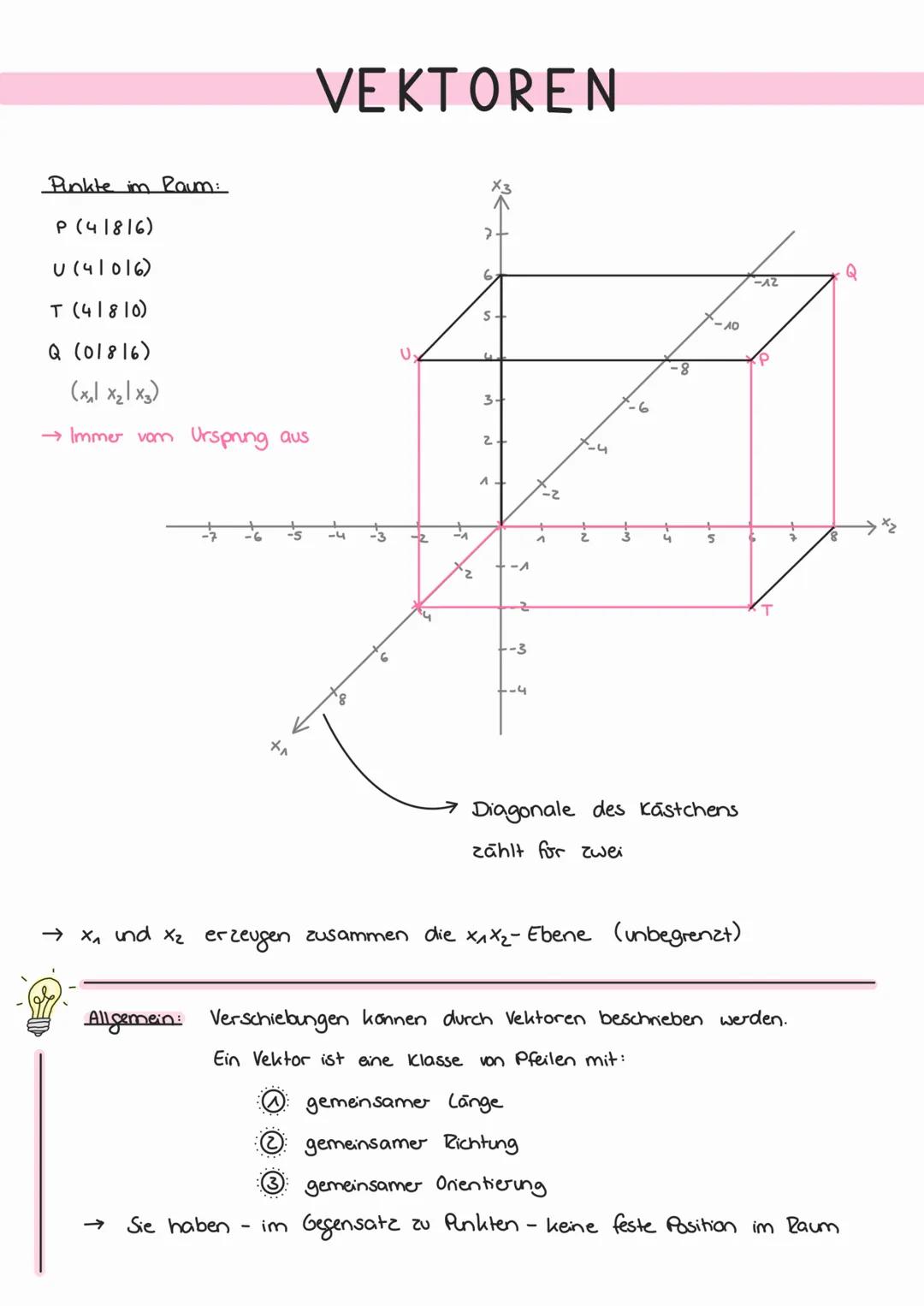
Punktproben bei Ebenen

Um zu prüfen, ob ein Punkt auf einer Ebene liegt, machst du eine Punktprobe. Das ist wie ein mathematischer Realitätscheck!

Setze die Koordinaten des Punktes in die Ebenengleichung ein. Du bekommst ein Gleichungssystem mit den Parametern r und s. Löse es systematisch auf.

Im Beispiel mit den Punkten A(3|0|2), B(5|1|7), C(6|2|5) und D(8|3|4) stellst du zunächst die Ebenengleichung mit A als Stützpunkt und AB⃗, AC⃗ als Spannvektoren auf.

Dann setzt du D ein und löst: Wenn das System eine eindeutige Lösung hat $wie t=1, s=1$, liegt der Punkt auf der Ebene. Das checkst du durch Einsetzen in die dritte Gleichung!

Kontrollmöglichkeit: Setze deine gefundenen Parameter immer in alle drei Gleichungen ein - nur wenn überall das Gleiche rauskommt, stimmt dein Ergebnis!

Orthogonalität und Skalarprodukt

Das Skalarprodukt ist ein super wichtiges Werkzeug, um zu prüfen, ob Vektoren senkrecht zueinander stehen. Du multiplizierst einfach die entsprechenden Komponenten und addierst alles zusammen.

Orthogonale Vektoren erkennst du daran, dass ihr Skalarprodukt gleich null ist: a⃗ · b⃗ = 0 ⟺ a⃗ ⊥ b⃗. Das ist besonders wichtig für rechtwinklige Dreiecke!

Bei einem Dreieck mit rechtem Winkel bei A berechnest du die Vektoren AB⃗ und AC⃗. Ist ihr Skalarprodukt null, hast du einen rechten Winkel bewiesen.

Zwei Geraden sind orthogonal, wenn ihre Richtungsvektoren senkrecht zueinander stehen. Das prüfst du genauso mit dem Skalarprodukt der Richtungsvektoren.

Praxistipp: Skalarprodukt = 0 bedeutet immer "senkrecht". Das ist dein wichtigster Test für Orthogonalität in Klassenarbeiten!

Vektorbeträge und Normalenvektoren

Der Betrag eines Vektors gibt dessen Länge an. Die Formel kennst du vom Satz des Pythagoras: |AB⃗| = √$(b₁-a₁)² + (b₂-a₂)² + (b₃-a₃)²$. Das ist gleichzeitig der Abstand zwischen den Punkten A und B.

Für Winkelberechnungen zwischen Vektoren brauchst du die Formel: cos(α) = (a⃗ · b⃗)/(|a⃗| · |b⃗|). Den Winkel bekommst du dann mit cos⁻¹.

Ein Normalenvektor einer Ebene steht senkrecht auf allen Vektoren in der Ebene. Er ist orthogonal zu beiden Spannvektoren der Ebene.

Die Normalenform einer Ebene lautet: E: $x⃗ - p⃗$ · n⃗ = 0. Hier ist p⃗ der Stützvektor und n⃗ der Normalenvektor. x⃗ steht für jeden beliebigen Punkt auf der Ebene.

Wichtig: Der Normalenvektor zeigt immer senkrecht von der Ebene weg - wie ein Pfeil, der aus einer Tischplatte herausragt!

Koordinatenform und Spurpunkte

Die Koordinatenform einer Ebene sieht so aus: ax₁ + bx₂ + cx₃ = d. Der große Vorteil: Du kannst den Normalenvektor direkt ablesen - er ist n⃗ = (a|b|c).

Spurpunkte sind die Schnittpunkte der Ebene mit den Koordinatenachsen. Sie helfen dir, die Ebene zu visualisieren. Für den x₁-Achsen-Spurpunkt setzt du x₂ = 0 und x₃ = 0.

Beispiel: Bei E: 3x₁ + 9x₂ - 2x₃ = 18 bekommst du die Spurpunkte S₁(6|0|0), S₂(0|2|0) und S₃(0|0|-9).

Manchmal geht eine Ebene durch den Ursprung $dann ist d = 0$. In diesem Fall haben alle Spurpunkte die Koordinaten (0|0|0) - die Ebene schneidet alle Achsen im Nullpunkt.

Visualisierungshilfe: Spurpunkte sind wie die "Eckpunkte" deiner Ebene auf den Achsen - sie zeigen dir, wo die Ebene das Koordinatensystem "durchbohrt"!

Ebenenformen umwandeln

Du kannst zwischen verschiedenen Ebenenformen hin und her wechseln. Das ist besonders für Klassenarbeiten wichtig!

Von der Parameterform zur Normalenform: Der Stützvektor p⃗ bleibt gleich. Den Normalenvektor n⃗ findest du, indem du ein Gleichungssystem aufstellst: Beide Spannvektoren müssen orthogonal zu n⃗ sein.

Das bedeutet: u⃗ · n⃗ = 0 und v⃗ · n⃗ = 0. Du setzt einen Parameter $z.B. n₂ = λ$ und löst nach den anderen auf. Oft multiplizierst du am Ende mit einer ganzen Zahl, um Brüche zu vermeiden.

Für die Koordinatenform setzt du den Stützpunkt in die Normalenform ein, um d zu bestimmen. Dann hast du deine fertige Gleichung: ax₁ + bx₂ + cx₃ = d.

Rechentrick: Wähle für deinen Parameter eine einfache Zahl (wie 1 oder 3) - das macht die Rechnungen übersichtlicher!

Lagebeziehungen Gerade-Ebene

Eine Gerade und eine Ebene können sich auf drei verschiedene Arten begegnen. Das musst du systematisch untersuchen können!

Durchstoßpunkt: Die Gerade schneidet die Ebene in genau einem Punkt. Setze die Geradengleichung in die Ebenengleichung ein und löse nach dem Parameter auf.

Parallel: Die Gerade verläuft parallel zur Ebene ohne sie zu schneiden. Das passiert, wenn das Einsetzen zu einem Widerspruch führt $wie 2 = 6$.

Gerade liegt in der Ebene: Unendlich viele Schnittpunkte. Das erkennst du daran, dass beim Einsetzen eine wahre Aussage wie 0 = 0 entsteht - jeder Punkt der Geraden liegt auf der Ebene.

Im Beispiel E: x₁ + 2x₂ - x₃ = 6 und g: x⃗ = (0|1|2) + t·(2|1|2) führt das Einsetzen zu t = 3, also zum Schnittpunkt S(6|4|8).

Prüfstrategie: Einsetzen und schauen: Eine Zahl für t = Schnittpunkt, Widerspruch = parallel, wahre Aussage = Gerade in Ebene!