Zusammenfassung
Melde dich an, um den Inhalt freizuschaltenEs ist kostenlos!
Zugriff auf alle Dokumente
Verbessere deine Noten
Werde Teil der Community
Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie
Bedeutende Theaterstücke der deutschen Literatur
Deutsche Kulturelle Identität
Deutsche Dichter und Lyrik
Deutsche Bildungsliteratur
Goethes Hauptwerke
Deutsche Kunstströmungen und Bewegungen
Deutsche Kurzgeschichten der Nachkriegszeit
Deutsche Sprachgrundlagen
Kafkas Hauptwerke
Moderne Deutsche Familienstrukturen
Alle Themen
Neuronale Kommunikationssysteme
RNA-Biologie und Genexpression
Zellulärer Energiestoffwechsel
Autotrophe Energieprozesse
Membranumschlossene Organellen
Ökologische Systeme und Wechselwirkungen
DNA-Replikation und -Reparatur
Organsysteme des Menschen
Vererbungsmuster und Vererbungsprinzipien
Enzymstruktur und -regulation
Alle Themen
Classic and Contemporary Novels
Literary Character Analysis
Verb Forms and Functions
Classic Dramatic Literature
Thesis Development and Structure
Rhetorical Theory and Practice
Evidence Analysis and Integration
Common Expression Pairs
English Language Components
Reading Analysis and Interpretation
Alle Themen
Eigenschaften von Funktionsgraphen
Quadratische Ausdrücke und Formen
Wahrscheinlichkeitsverteilungen und Zufallsvariablen
Grundlegende Ableitungsregeln
Lineare Gleichungen und Graphen
Methoden der Funktionsoptimierung
Flächenberechnungsmethoden mit Integralen
Geometrische Systeme und Modelle
Ableitungen und Anwendungen
Eigenschaften von Potenzen und Logarithmen
Alle Themen
Nationalsozialismus und Holocaust 1933-1945
Deutsche Sozialbewegungen und gesellschaftlicher Wandel
Moderne Demokratische Revolutionen
Weltkriege und Friedensverträge
Europäische Monarchen und Staatsmänner
Globale Spannungen im Kalten Krieg
Die Europäische Renaissance und Aufklärung
Historische Quellen und Dokumentation
Die Ära der Weltkriege und ihre Auswirkungen
Moderne Militärische Konflikte
Alle Themen
4.588
•
25. Dez. 2025
•
Chiara
@chiara_pcki
Zusammenfassung





Unser KI-Begleiter ist speziell auf die Bedürfnisse von Schülern zugeschnitten. Basierend auf den Millionen von Inhalten, die wir auf der Plattform haben, können wir den Schülern wirklich sinnvolle und relevante Antworten geben. Aber es geht nicht nur um Antworten, sondern der Begleiter führt die Schüler auch durch ihre täglichen Lernherausforderungen, mit personalisierten Lernplänen, Quizfragen oder Inhalten im Chat und einer 100% Personalisierung basierend auf den Fähigkeiten und Entwicklungen der Schüler.
Du kannst dir die App im Google Play Store und im Apple App Store herunterladen.
Ja, du hast kostenlosen Zugriff auf Inhalte in der App und auf unseren KI-Begleiter. Zum Freischalten bestimmter Features in der App kannst du Knowunity Pro erwerben.
App Store
Google Play
Die App ist sehr leicht und gut gestaltet. Habe bis jetzt alles gefunden, nachdem ich gesucht habe und aus den Präsentationen echt viel lernen können! Die App werde ich auf jeden Fall für eine Klassenarbeit verwenden! Und als eigene Inspiration hilft sie natürlich auch sehr.
Stefan S
iOS user
Diese App ist wirklich echt super. Es gibt so viele Lernzettel und Hilfen, […]. Mein Problemfach ist zum Beispiel Französisch und die App hat mega viel Auswahl für Hilfe. Dank dieser App habe ich mich in Französisch verbessert. Ich würde diese jedem weiterempfehlen.
Samantha Klich
Android user
Wow ich bin wirklich komplett baff. Habe die App nur mal so ausprobiert, weil ich es schon oft in der Werbung gesehen habe und war absolut geschockt. Diese App ist DIE HILFE, die man sich für die Schule wünscht und vor allem werden so viele Sachen angeboten, wie z.B. Ausarbeitungen und Merkblätter, welche mir persönlich SEHR weitergeholfen haben.
Anna
iOS user
Ich finde Knowunity so grandios. Ich lerne wirklich für alles damit. Es gibt so viele verschiedene Lernzettel, die sehr gut erklärt sind!
Jana V
iOS user
Ich liebe diese App sie hilft mir vor jeder Arbeit kann Aufgaben kontrollieren sowie lösen und ist wirklich vielfältig verwendbar. Man kann mit diesem Fuchs auch normal reden so wie Probleme im echten Leben besprechen und er hilft einem. Wirklich sehr gut diese App kann ich nur weiter empfehlen, gerade für Menschen die etwas länger brauchen etwas zu verstehen!
Lena M
Android user
Ich finde Knowunity ist eine super App. Für die Schule ist sie ideal , wegen den Lernzetteln, Quizen und dem AI. Das gute an AI ist , dass er nicht direkt nur die Lösung ausspuckt sondern einen Weg zeigt wie man darauf kommt. Manchmal gibt er einem auch nur einen Tipp damit man selbst darauf kommt . Mir hilft Knowunity persönlich sehr viel und ich kann sie nur weiterempfehlen ☺️
Timo S
iOS user
Die App ist einfach super! Ich muss nur in die Suchleiste mein Thema eintragen und ich checke es sehr schnell. Ich muss nicht mehr 10 YouTube Videos gucken, um etwas zu verstehen und somit spare ich mir meine Zeit. Einfach zu empfehlen!!
Sudenaz Ocak
Android user
Diese App hat mich echt verbessert! In der Schule war ich richtig schlecht in Mathe und dank der App kann ich besser Mathe! Ich bin so dankbar, dass ihr die App gemacht habt.
Greenlight Bonnie
Android user
Ich benutze Knowunity schon sehr lange und meine Noten haben sich verbessert die App hilft mir bei Mathe,Englisch u.s.w. Ich bekomme Hilfe wenn ich sie brauche und bekomme sogar Glückwünsche für meine Arbeit Deswegen von mir 5 Sterne🫶🏼
Julia S
Android user
Also die App hat mir echt in super vielen Fächern geholfen! Ich hatte in der Mathe Arbeit davor eine 3+ und habe nur durch den School GPT und die Lernzettek auf der App eine 1-3 in Mathe geschafft…Ich bin Mega glücklich darüber also ja wircklich eine super App zum lernen und es spart sehr viel Heit dass man mehr Freizeit hat!
Marcus B
iOS user
Mit dieser App hab ich bessere Noten bekommen. Bessere Lernzettel gekriegt. Ich habe die App benutzt, als ich die Fächer nicht ganz verstanden habe,diese App ist ein würcklich GameChanger für die Schule, Hausaufgaben
Sarah L
Android user
Hatte noch nie so viel Spaß beim Lernen und der School Bot macht super Aufschriebe die man Herunterladen kann total Übersichtlich und Lehreich. Bin begeistert.
Hans T
iOS user
Die App ist sehr leicht und gut gestaltet. Habe bis jetzt alles gefunden, nachdem ich gesucht habe und aus den Präsentationen echt viel lernen können! Die App werde ich auf jeden Fall für eine Klassenarbeit verwenden! Und als eigene Inspiration hilft sie natürlich auch sehr.
Stefan S
iOS user
Diese App ist wirklich echt super. Es gibt so viele Lernzettel und Hilfen, […]. Mein Problemfach ist zum Beispiel Französisch und die App hat mega viel Auswahl für Hilfe. Dank dieser App habe ich mich in Französisch verbessert. Ich würde diese jedem weiterempfehlen.
Samantha Klich
Android user
Wow ich bin wirklich komplett baff. Habe die App nur mal so ausprobiert, weil ich es schon oft in der Werbung gesehen habe und war absolut geschockt. Diese App ist DIE HILFE, die man sich für die Schule wünscht und vor allem werden so viele Sachen angeboten, wie z.B. Ausarbeitungen und Merkblätter, welche mir persönlich SEHR weitergeholfen haben.
Anna
iOS user
Ich finde Knowunity so grandios. Ich lerne wirklich für alles damit. Es gibt so viele verschiedene Lernzettel, die sehr gut erklärt sind!
Jana V
iOS user
Ich liebe diese App sie hilft mir vor jeder Arbeit kann Aufgaben kontrollieren sowie lösen und ist wirklich vielfältig verwendbar. Man kann mit diesem Fuchs auch normal reden so wie Probleme im echten Leben besprechen und er hilft einem. Wirklich sehr gut diese App kann ich nur weiter empfehlen, gerade für Menschen die etwas länger brauchen etwas zu verstehen!
Lena M
Android user
Ich finde Knowunity ist eine super App. Für die Schule ist sie ideal , wegen den Lernzetteln, Quizen und dem AI. Das gute an AI ist , dass er nicht direkt nur die Lösung ausspuckt sondern einen Weg zeigt wie man darauf kommt. Manchmal gibt er einem auch nur einen Tipp damit man selbst darauf kommt . Mir hilft Knowunity persönlich sehr viel und ich kann sie nur weiterempfehlen ☺️
Timo S
iOS user
Die App ist einfach super! Ich muss nur in die Suchleiste mein Thema eintragen und ich checke es sehr schnell. Ich muss nicht mehr 10 YouTube Videos gucken, um etwas zu verstehen und somit spare ich mir meine Zeit. Einfach zu empfehlen!!
Sudenaz Ocak
Android user
Diese App hat mich echt verbessert! In der Schule war ich richtig schlecht in Mathe und dank der App kann ich besser Mathe! Ich bin so dankbar, dass ihr die App gemacht habt.
Greenlight Bonnie
Android user
Ich benutze Knowunity schon sehr lange und meine Noten haben sich verbessert die App hilft mir bei Mathe,Englisch u.s.w. Ich bekomme Hilfe wenn ich sie brauche und bekomme sogar Glückwünsche für meine Arbeit Deswegen von mir 5 Sterne🫶🏼
Julia S
Android user
Also die App hat mir echt in super vielen Fächern geholfen! Ich hatte in der Mathe Arbeit davor eine 3+ und habe nur durch den School GPT und die Lernzettek auf der App eine 1-3 in Mathe geschafft…Ich bin Mega glücklich darüber also ja wircklich eine super App zum lernen und es spart sehr viel Heit dass man mehr Freizeit hat!
Marcus B
iOS user
Mit dieser App hab ich bessere Noten bekommen. Bessere Lernzettel gekriegt. Ich habe die App benutzt, als ich die Fächer nicht ganz verstanden habe,diese App ist ein würcklich GameChanger für die Schule, Hausaufgaben
Sarah L
Android user
Hatte noch nie so viel Spaß beim Lernen und der School Bot macht super Aufschriebe die man Herunterladen kann total Übersichtlich und Lehreich. Bin begeistert.
Hans T
iOS user

Zugriff auf alle Dokumente
Verbessere deine Noten
Werde Teil der Community
Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Zugriff auf alle Dokumente
Verbessere deine Noten
Werde Teil der Community
Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie

Zugriff auf alle Dokumente
Verbessere deine Noten
Werde Teil der Community
Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und die Datenschutzrichtlinie
Unser KI-Begleiter ist speziell auf die Bedürfnisse von Schülern zugeschnitten. Basierend auf den Millionen von Inhalten, die wir auf der Plattform haben, können wir den Schülern wirklich sinnvolle und relevante Antworten geben. Aber es geht nicht nur um Antworten, sondern der Begleiter führt die Schüler auch durch ihre täglichen Lernherausforderungen, mit personalisierten Lernplänen, Quizfragen oder Inhalten im Chat und einer 100% Personalisierung basierend auf den Fähigkeiten und Entwicklungen der Schüler.
Du kannst dir die App im Google Play Store und im Apple App Store herunterladen.
Ja, du hast kostenlosen Zugriff auf Inhalte in der App und auf unseren KI-Begleiter. Zum Freischalten bestimmter Features in der App kannst du Knowunity Pro erwerben.
175
Smarte Tools NEU
Verwandle diese Notizen in: ✓ 50+ Übungsaufgaben ✓ Interaktive Karteikarten ✓ Vollständige Probeklausur ✓ Aufsatz-Gliederungen
Vertiefte Erklärung des pythagoreischen Theorems mit Beispielen zu pythagoreischen Zahlen tripeln und Berechnungen der Hypotenuse und Katheten. Ideal für Schüler, die die Grundlagen der Geometrie verstehen möchten.
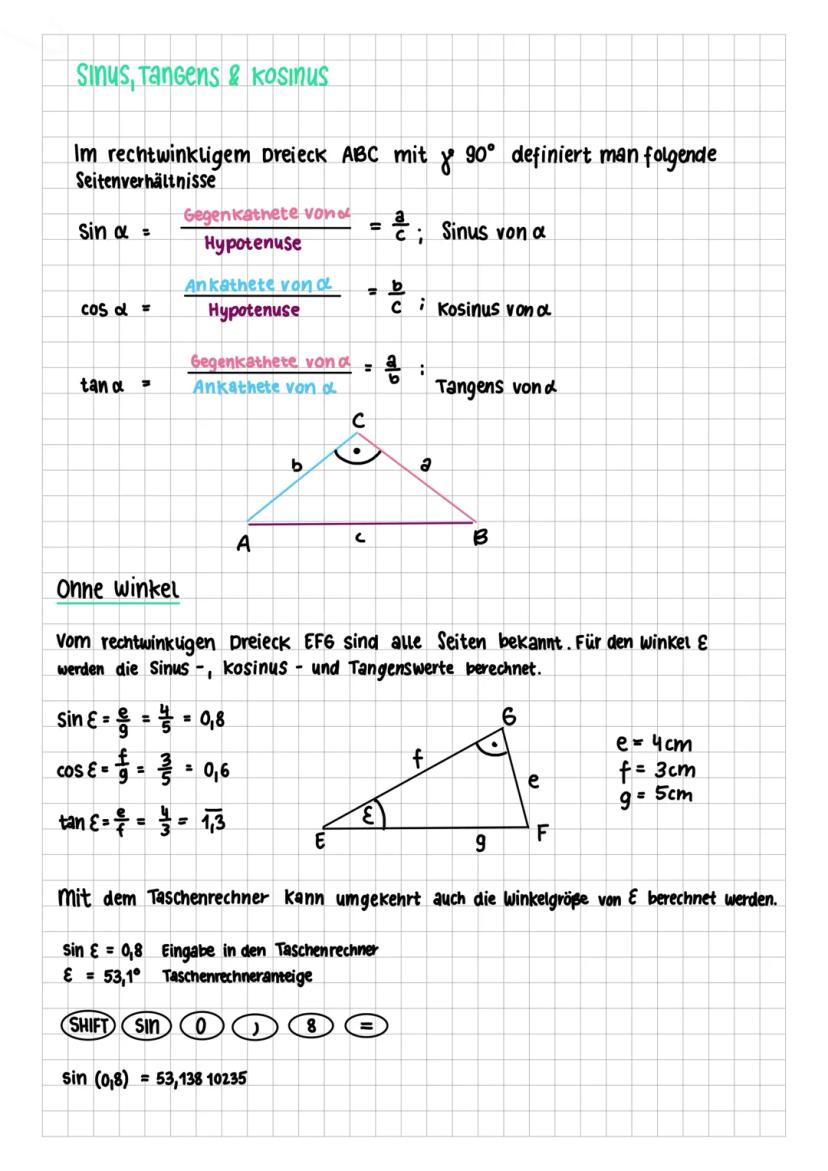
Entdecken Sie die Grundlagen der trigonometrischen Funktionen (Sinus, Kosinus, Tangens) und deren Anwendung in rechtwinkligen Dreiecken. Diese Zusammenfassung behandelt die Sinusregel, Kosinusregel und bietet praktische Beispiele zur Berechnung von Seiten und Winkeln. Ideal für Schüler, die sich auf Prüfungen vorbereiten oder ihr Verständnis der Trigonometrie vertiefen möchten.
Entdecken Sie die Grundlagen der Trigonometrie, einschließlich der Berechnung von Winkeln und Seitenlängen in rechtwinkligen und gleichschenkligen Dreiecken. Lernen Sie die Anwendung des Satzes des Pythagoras sowie die Formeln für Volumen und Oberfläche von Zylindern und Pyramiden. Ideal für Schüler, die sich auf Mathematikprüfungen vorbereiten.
Entdecke die grundlegenden trigonometrischen Beziehungen und Formeln für rechtwinklige und allgemeine Dreiecke. Diese Zusammenfassung behandelt Sinus, Kosinus, Tangens, den Sinussatz und Kosinussatz sowie deren Anwendungen in der Geometrie. Ideal für Schüler der 9. Klasse im Gymnasium, die sich auf Prüfungen vorbereiten oder ihr Verständnis der Trigonometrie vertiefen möchten.
Entdecken Sie den Höhensatz mit klaren Beispielen und Berechnungen. Lernen Sie, wie das Quadrat der Höhe h gleich dem Produkt der Abschnitte der Hypotenuse p und q ist. Ideal für Studierende der Geometrie. Typ: Zusammenfassung.
Erfahren Sie alles über den Pythagoreischen Lehrsatz: die allgemeine Formel \(a^2 + b^2 = c^2\), Berechnung der Hypotenuse und der Katheten mit anschaulichen Beispielen. Ideal für Schüler, die ihre Kenntnisse in Geometrie vertiefen möchten.
App Store
Google Play
Die App ist sehr leicht und gut gestaltet. Habe bis jetzt alles gefunden, nachdem ich gesucht habe und aus den Präsentationen echt viel lernen können! Die App werde ich auf jeden Fall für eine Klassenarbeit verwenden! Und als eigene Inspiration hilft sie natürlich auch sehr.
Stefan S
iOS user
Diese App ist wirklich echt super. Es gibt so viele Lernzettel und Hilfen, […]. Mein Problemfach ist zum Beispiel Französisch und die App hat mega viel Auswahl für Hilfe. Dank dieser App habe ich mich in Französisch verbessert. Ich würde diese jedem weiterempfehlen.
Samantha Klich
Android user
Wow ich bin wirklich komplett baff. Habe die App nur mal so ausprobiert, weil ich es schon oft in der Werbung gesehen habe und war absolut geschockt. Diese App ist DIE HILFE, die man sich für die Schule wünscht und vor allem werden so viele Sachen angeboten, wie z.B. Ausarbeitungen und Merkblätter, welche mir persönlich SEHR weitergeholfen haben.
Anna
iOS user
Ich finde Knowunity so grandios. Ich lerne wirklich für alles damit. Es gibt so viele verschiedene Lernzettel, die sehr gut erklärt sind!
Jana V
iOS user
Ich liebe diese App sie hilft mir vor jeder Arbeit kann Aufgaben kontrollieren sowie lösen und ist wirklich vielfältig verwendbar. Man kann mit diesem Fuchs auch normal reden so wie Probleme im echten Leben besprechen und er hilft einem. Wirklich sehr gut diese App kann ich nur weiter empfehlen, gerade für Menschen die etwas länger brauchen etwas zu verstehen!
Lena M
Android user
Ich finde Knowunity ist eine super App. Für die Schule ist sie ideal , wegen den Lernzetteln, Quizen und dem AI. Das gute an AI ist , dass er nicht direkt nur die Lösung ausspuckt sondern einen Weg zeigt wie man darauf kommt. Manchmal gibt er einem auch nur einen Tipp damit man selbst darauf kommt . Mir hilft Knowunity persönlich sehr viel und ich kann sie nur weiterempfehlen ☺️
Timo S
iOS user
Die App ist einfach super! Ich muss nur in die Suchleiste mein Thema eintragen und ich checke es sehr schnell. Ich muss nicht mehr 10 YouTube Videos gucken, um etwas zu verstehen und somit spare ich mir meine Zeit. Einfach zu empfehlen!!
Sudenaz Ocak
Android user
Diese App hat mich echt verbessert! In der Schule war ich richtig schlecht in Mathe und dank der App kann ich besser Mathe! Ich bin so dankbar, dass ihr die App gemacht habt.
Greenlight Bonnie
Android user
Ich benutze Knowunity schon sehr lange und meine Noten haben sich verbessert die App hilft mir bei Mathe,Englisch u.s.w. Ich bekomme Hilfe wenn ich sie brauche und bekomme sogar Glückwünsche für meine Arbeit Deswegen von mir 5 Sterne🫶🏼
Julia S
Android user
Also die App hat mir echt in super vielen Fächern geholfen! Ich hatte in der Mathe Arbeit davor eine 3+ und habe nur durch den School GPT und die Lernzettek auf der App eine 1-3 in Mathe geschafft…Ich bin Mega glücklich darüber also ja wircklich eine super App zum lernen und es spart sehr viel Heit dass man mehr Freizeit hat!
Marcus B
iOS user
Mit dieser App hab ich bessere Noten bekommen. Bessere Lernzettel gekriegt. Ich habe die App benutzt, als ich die Fächer nicht ganz verstanden habe,diese App ist ein würcklich GameChanger für die Schule, Hausaufgaben
Sarah L
Android user
Hatte noch nie so viel Spaß beim Lernen und der School Bot macht super Aufschriebe die man Herunterladen kann total Übersichtlich und Lehreich. Bin begeistert.
Hans T
iOS user
Die App ist sehr leicht und gut gestaltet. Habe bis jetzt alles gefunden, nachdem ich gesucht habe und aus den Präsentationen echt viel lernen können! Die App werde ich auf jeden Fall für eine Klassenarbeit verwenden! Und als eigene Inspiration hilft sie natürlich auch sehr.
Stefan S
iOS user
Diese App ist wirklich echt super. Es gibt so viele Lernzettel und Hilfen, […]. Mein Problemfach ist zum Beispiel Französisch und die App hat mega viel Auswahl für Hilfe. Dank dieser App habe ich mich in Französisch verbessert. Ich würde diese jedem weiterempfehlen.
Samantha Klich
Android user
Wow ich bin wirklich komplett baff. Habe die App nur mal so ausprobiert, weil ich es schon oft in der Werbung gesehen habe und war absolut geschockt. Diese App ist DIE HILFE, die man sich für die Schule wünscht und vor allem werden so viele Sachen angeboten, wie z.B. Ausarbeitungen und Merkblätter, welche mir persönlich SEHR weitergeholfen haben.
Anna
iOS user
Ich finde Knowunity so grandios. Ich lerne wirklich für alles damit. Es gibt so viele verschiedene Lernzettel, die sehr gut erklärt sind!
Jana V
iOS user
Ich liebe diese App sie hilft mir vor jeder Arbeit kann Aufgaben kontrollieren sowie lösen und ist wirklich vielfältig verwendbar. Man kann mit diesem Fuchs auch normal reden so wie Probleme im echten Leben besprechen und er hilft einem. Wirklich sehr gut diese App kann ich nur weiter empfehlen, gerade für Menschen die etwas länger brauchen etwas zu verstehen!
Lena M
Android user
Ich finde Knowunity ist eine super App. Für die Schule ist sie ideal , wegen den Lernzetteln, Quizen und dem AI. Das gute an AI ist , dass er nicht direkt nur die Lösung ausspuckt sondern einen Weg zeigt wie man darauf kommt. Manchmal gibt er einem auch nur einen Tipp damit man selbst darauf kommt . Mir hilft Knowunity persönlich sehr viel und ich kann sie nur weiterempfehlen ☺️
Timo S
iOS user
Die App ist einfach super! Ich muss nur in die Suchleiste mein Thema eintragen und ich checke es sehr schnell. Ich muss nicht mehr 10 YouTube Videos gucken, um etwas zu verstehen und somit spare ich mir meine Zeit. Einfach zu empfehlen!!
Sudenaz Ocak
Android user
Diese App hat mich echt verbessert! In der Schule war ich richtig schlecht in Mathe und dank der App kann ich besser Mathe! Ich bin so dankbar, dass ihr die App gemacht habt.
Greenlight Bonnie
Android user
Ich benutze Knowunity schon sehr lange und meine Noten haben sich verbessert die App hilft mir bei Mathe,Englisch u.s.w. Ich bekomme Hilfe wenn ich sie brauche und bekomme sogar Glückwünsche für meine Arbeit Deswegen von mir 5 Sterne🫶🏼
Julia S
Android user
Also die App hat mir echt in super vielen Fächern geholfen! Ich hatte in der Mathe Arbeit davor eine 3+ und habe nur durch den School GPT und die Lernzettek auf der App eine 1-3 in Mathe geschafft…Ich bin Mega glücklich darüber also ja wircklich eine super App zum lernen und es spart sehr viel Heit dass man mehr Freizeit hat!
Marcus B
iOS user
Mit dieser App hab ich bessere Noten bekommen. Bessere Lernzettel gekriegt. Ich habe die App benutzt, als ich die Fächer nicht ganz verstanden habe,diese App ist ein würcklich GameChanger für die Schule, Hausaufgaben
Sarah L
Android user
Hatte noch nie so viel Spaß beim Lernen und der School Bot macht super Aufschriebe die man Herunterladen kann total Übersichtlich und Lehreich. Bin begeistert.
Hans T
iOS user