Koordinatenumwandlungen
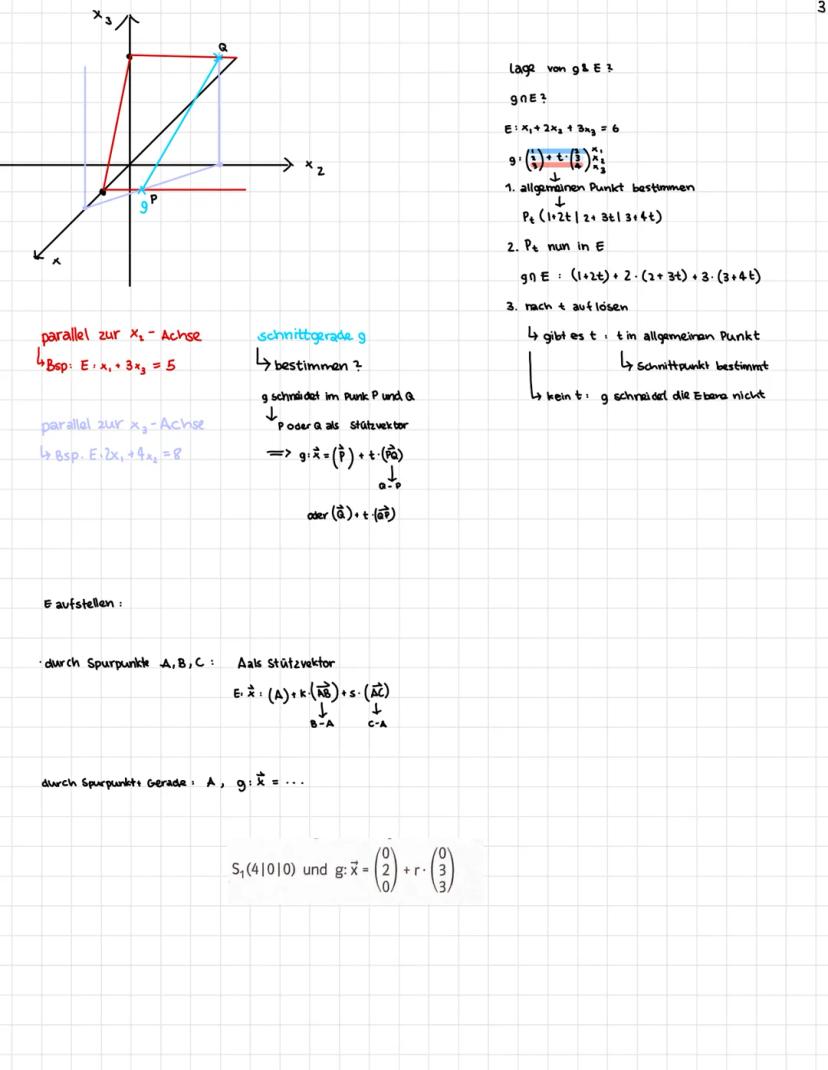
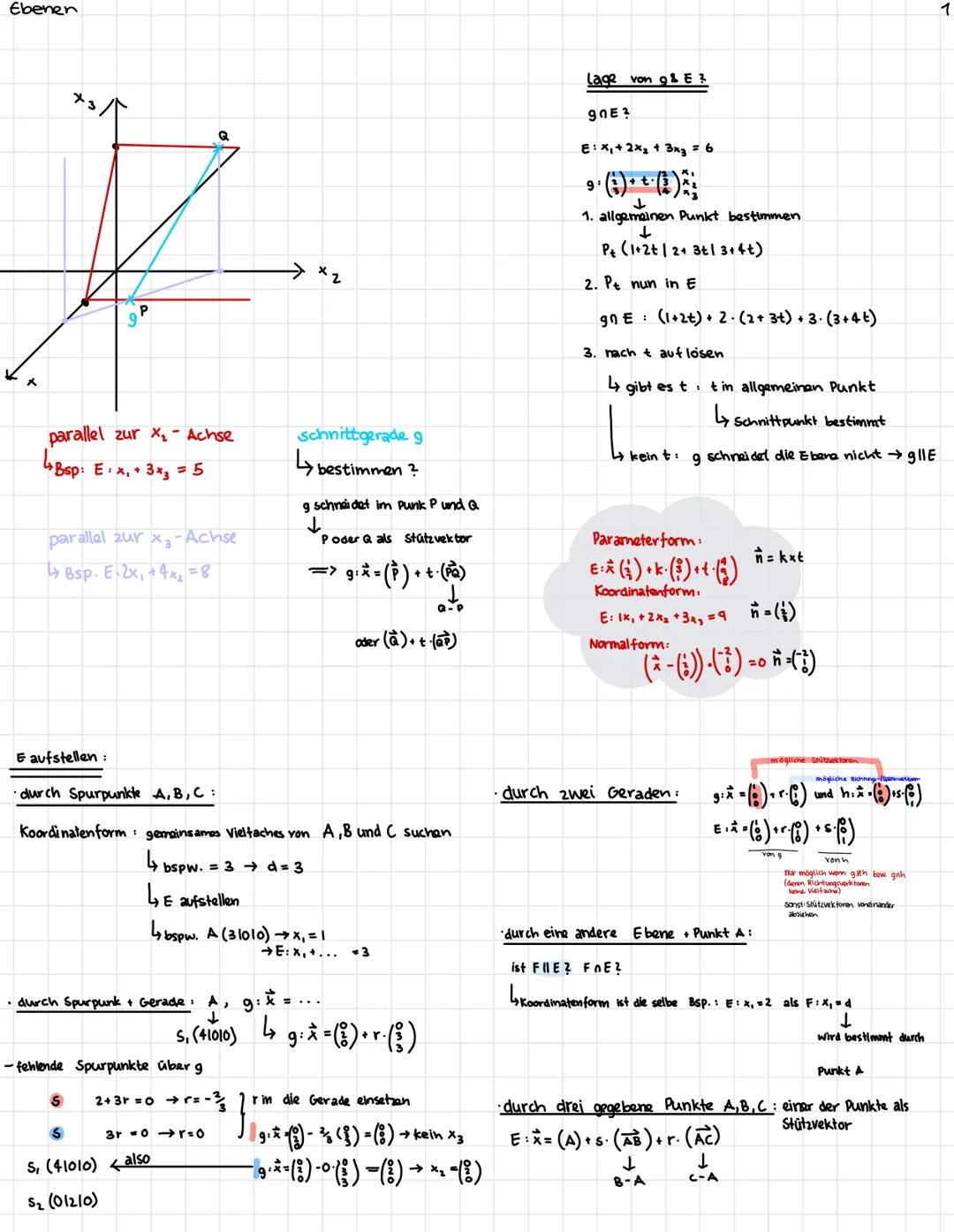
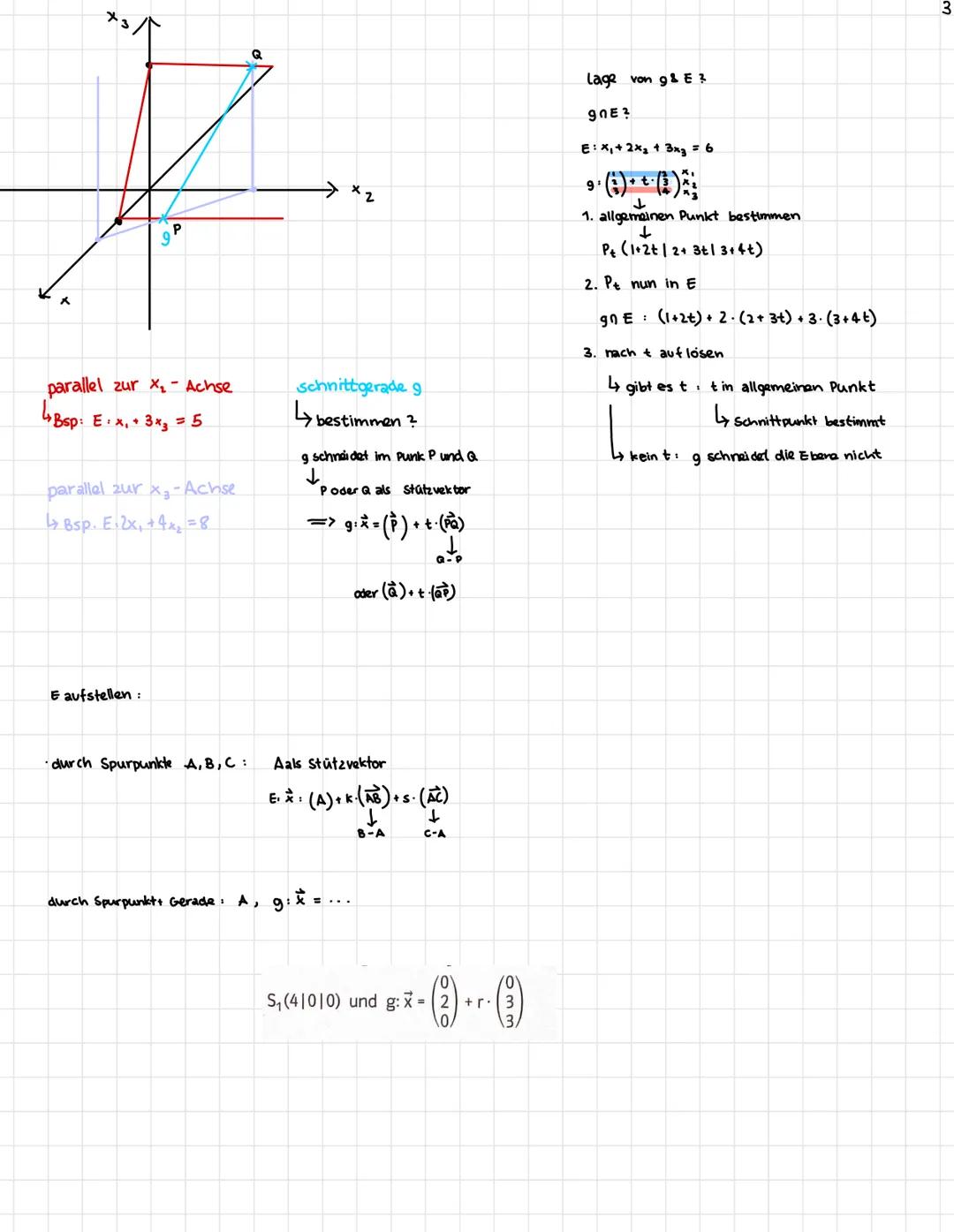
Von Parameterform zu Koordinatenform gehst du über das Vektorprodukt der Richtungsvektoren. Das gibt dir den Normalenvektor n⃗ = (a|b|c), woraus die Koordinatenform ax₁ + bx₂ + cx₃ = d wird. Den Wert d bestimmst du, indem du den Stützvektor einsetzt.
Von Normalform zu Koordinatenform ist noch einfacher. Die Normalform n⃗ · x⃗−a⃗ = 0 multiplizierst du aus: n⃗ · x⃗ - n⃗ · a⃗ = 0. Das wird direkt zu ax₁ + bx₂ + cx₃ = d, wobei d = n⃗ · a⃗ ist.
Bei parallel oder identisch vergleichst du die Normalenvektoren. Bei E: 3x₁ + 2x₂ + 2x₃ = 8 und F: 6x₁ + 4x₂ + 4x₃ = 16 ist der Normalenvektor von F das Doppelte von E. Da auch d verdoppelt ist (8 → 16), sind die Ebenen identisch.
Echt parallel wären sie, wenn nur die Normalenvektoren proportional sind, aber d nicht im gleichen Verhältnis steht. Dann haben die Ebenen überall den gleichen Abstand.
Check: Normalenvektoren proportional = parallel, d-Werte auch proportional = identisch!