Grundbegriffe der Stochastik

Stochastik klingt kompliziert, ist aber eigentlich nur das mathematische Werkzeug für alles, was mit Zufall zu tun hat. Beim Münzwurf ist jedes einzelne Resultat (Kopf oder Zahl) ein Ergebnis, während der Ergebnisraum Ω alle möglichen Ausgänge sammelt.

Es gibt drei wichtige Ereignis-Typen: Das unmögliche Ereignis (passiert nie), das sichere Ereignis (passiert immer) und das Gegenereignis (alles andere als dein gewünschtes Ergebnis). Die Wahrscheinlichkeit P(E) gibt dir an, wie wahrscheinlich dein Ereignis ist - zwischen 0 und 1.

Bei Laplace-Experimenten haben alle Ergebnisse die gleiche Chance. Die Formel ist super simpel: P(E) = Anzahl der gesuchten Möglichkeiten / Anzahl aller Möglichkeiten.

Baumdiagramme sind dein bester Freund bei mehrstufigen Experimenten. Du multiplizierst entlang eines Pfades und addierst verschiedene Pfade - so einfach ist das!

💡 Merktipp: Bei der Pfadregel denkst du wie beim Backen - entlang eines Rezepts multiplizierst du die Zutaten, für verschiedene Kuchen addierst du die Mengen!

Vierfeldertafel und bedingte Wahrscheinlichkeit

Die Vierfeldertafel ist wie ein Koordinatensystem für zwei Ereignisse A und B. Du trägst alle Kombinationen ein und hast sofort den Überblick über alle Wahrscheinlichkeiten.

Du kannst jede Vierfeldertafel auch als Baumdiagramm darstellen. Das hilft dir, die Zusammenhänge zwischen den Ereignissen besser zu verstehen und Fehler zu vermeiden.

Bedingte Wahrscheinlichkeit bedeutet: Wie wahrscheinlich ist Ereignis F, wenn ich schon weiß, dass E eingetreten ist? Die Formel lautet: P_E(F) = P(E ∩ F) / P(E). Das ist wie bei einer WhatsApp-Gruppe - die Wahrscheinlichkeit einer Antwort ändert sich, je nachdem wer die erste Nachricht geschrieben hat.

💡 Merktipp: Bedingte Wahrscheinlichkeit ist wie ein Filter - du schaust nur noch auf den Teil der Welt, wo deine Bedingung erfüllt ist!

Unabhängigkeit und Bayes

Stochastische Unabhängigkeit liegt vor, wenn sich zwei Ereignisse gegenseitig nicht beeinflussen. Mathematisch: P(A∩B) = P(A) · P(B). Das ist wie bei unabhängigen Netflix-Accounts - was du schaust, beeinflusst nicht, was dein Mitbewohner sieht.

Die Regel von Bayes dreht die Zeit um: Du beobachtest ein Ergebnis und fragst dich, welche Ursache am wahrscheinlichsten war. A posteriori bedeutet "nach der Beobachtung", a priori "vor der Beobachtung".

Das klassische Beispiel: Du würfelst eine 3 und fragst dich, ob du mit dem normalen Würfel oder dem speziellen Quader gewürfelt hast. Bayes hilft dir, aus dem Ergebnis auf die Ursache zu schließen.

Die a posteriori-Wahrscheinlichkeit berechnest du mit: Wahrscheinlichkeit des Pfades / totale Wahrscheinlichkeit des beobachteten Ergebnisses.

💡 Merktipp: Bayes ist wie Detektivarbeit - du siehst das Ergebnis und schließt rückwärts auf den wahrscheinlichsten "Täter"!

Erwartungswert und Kombinatorik

Der Erwartungswert ist das, was du durchschnittlich erwarten kannst, wenn du ein Experiment oft wiederholst. Bei einer Urliste berechnest du den Mittelwert durch Addition und Division, bei Zufallsgrößen gewichtest du jeden Wert mit seiner Wahrscheinlichkeit.

Die Standardabweichung zeigt dir, wie stark die Werte um den Erwartungswert streuen. Je größer die Standardabweichung, desto unvorhersagbarer sind deine Ergebnisse.

Kombinatorik beantwortet die Frage: "Auf wie viele Arten kann ich etwas machen?" Die Produktregel sagt: Multipliziere die Möglichkeiten aller Stufen. Bei mehrstufigen Experimenten wird das richtig praktisch.

Die wichtigsten Formeln: Mit Zurücklegen und Reihenfolge = n^k, ohne Zurücklegen mit Reihenfolge = n!/$n-k$!, ohne Zurücklegen ohne Reihenfolge = Binomialkoeffizient (n über k).

💡 Merktipp: Frage dich immer: "Kommt die Kugel zurück in die Urne?" und "Ist mir die Reihenfolge wichtig?" - dann weißt du, welche Formel passt!

Binomialverteilung

Die Binomialverteilung ist dein Werkzeug für alle "Treffer oder Niete"-Situationen. Eine Bernoulli-Kette hat immer nur zwei mögliche Ausgänge und konstante Trefferwahrscheinlichkeit.

Die Grundformel lautet: B(n;p;k) = (n über k) · p^k · $1-p$^$n-k$. Dabei ist n die Anzahl der Versuche, p die Trefferwahrscheinlichkeit und k die Anzahl der Treffer. Am GTR nutzt du "binomPDF".

Für mehrere Wahrscheinlichkeiten addierst du oder verwendest die kumulierte Wahrscheinlichkeit F(n;p;k) mit "binomCDF" am GTR.

Erwartungswert μ = n·p und Standardabweichung σ = √$n·p·(1-p)$. Die Binomialverteilung wird mit größerem n flacher und symmetrischer, bei p=0,5 ist sie automatisch symmetrisch.

💡 Merktipp: Binomialverteilung passt perfekt für alle "Ja/Nein"-Fragen: Bestehe ich die Prüfung? Regnet es? Gewinnt mein Team?

Sigmaregel und Problemlösung

Die Sigmaregel gibt dir schnelle Näherungswerte: Ca. 68% aller Werte liegen im 1σ-Bereich, 95,4% im 2σ-Bereich und 99,7% im 3σ-Bereich um den Erwartungswert μ.

Die Laplace-Bedingung σ > 3 muss erfüllt sein, damit du die Sigmaregel anwenden darfst. Das schützt dich vor falschen Ergebnissen bei zu kleinen Stichproben.

Problemlösung bei Binomialverteilung: Für bekannte Wahrscheinlichkeiten setzt du alles in die Formel ein. Bei unbekannten Parametern probierst du systematisch Werte aus oder löst mit Logarithmus auf.

Das Logarithmus-Verfahren ist besonders elegant: Du löst die Bernoulli-Formel nach dem gesuchten Parameter auf und wendest den natürlichen Logarithmus an, um Exponenten "herunterzuholen".

💡 Merktipp: Die Sigmaregel ist wie ein Sicherheitsnetz - sie zeigt dir, wo 95% aller "normalen" Ergebnisse landen!

Zweiseitiger Signifikanztest

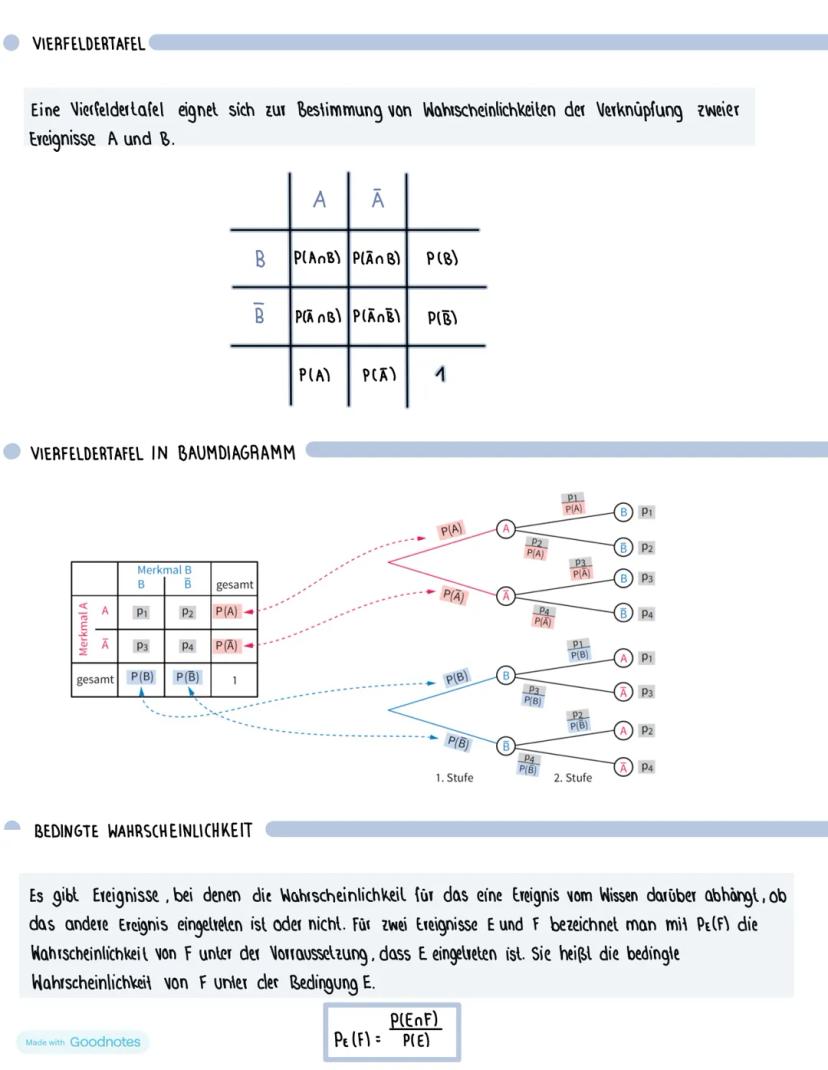
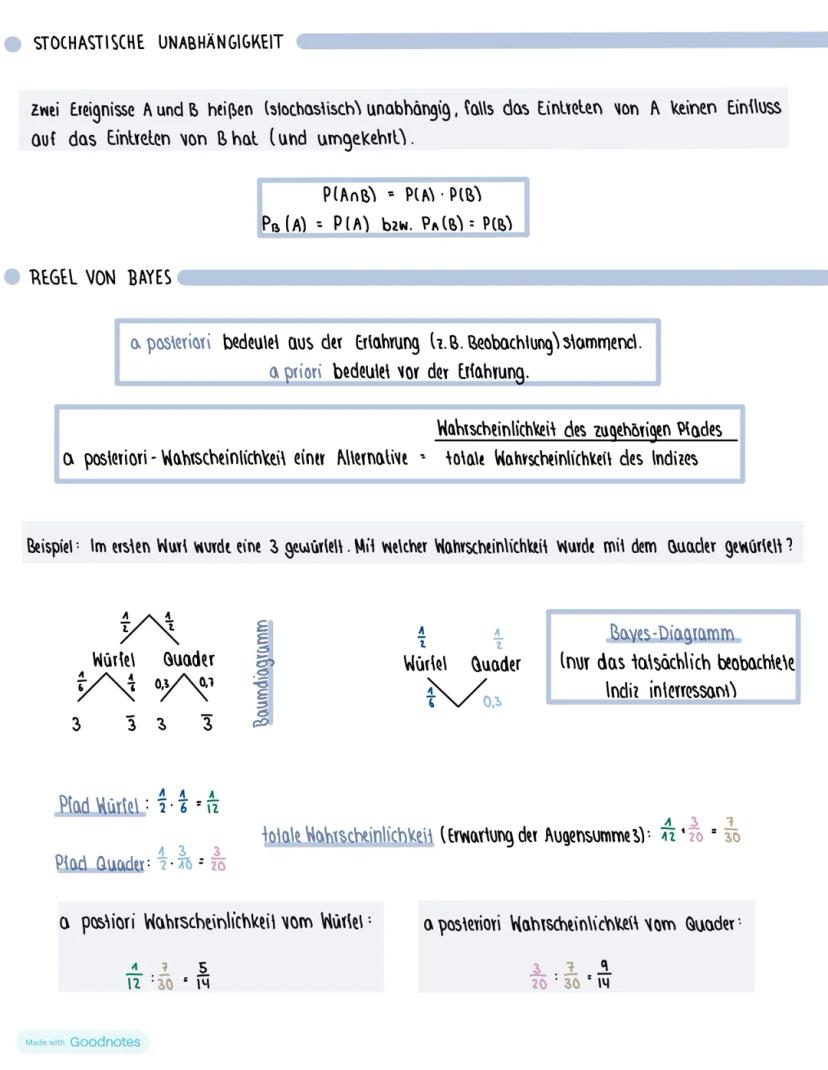
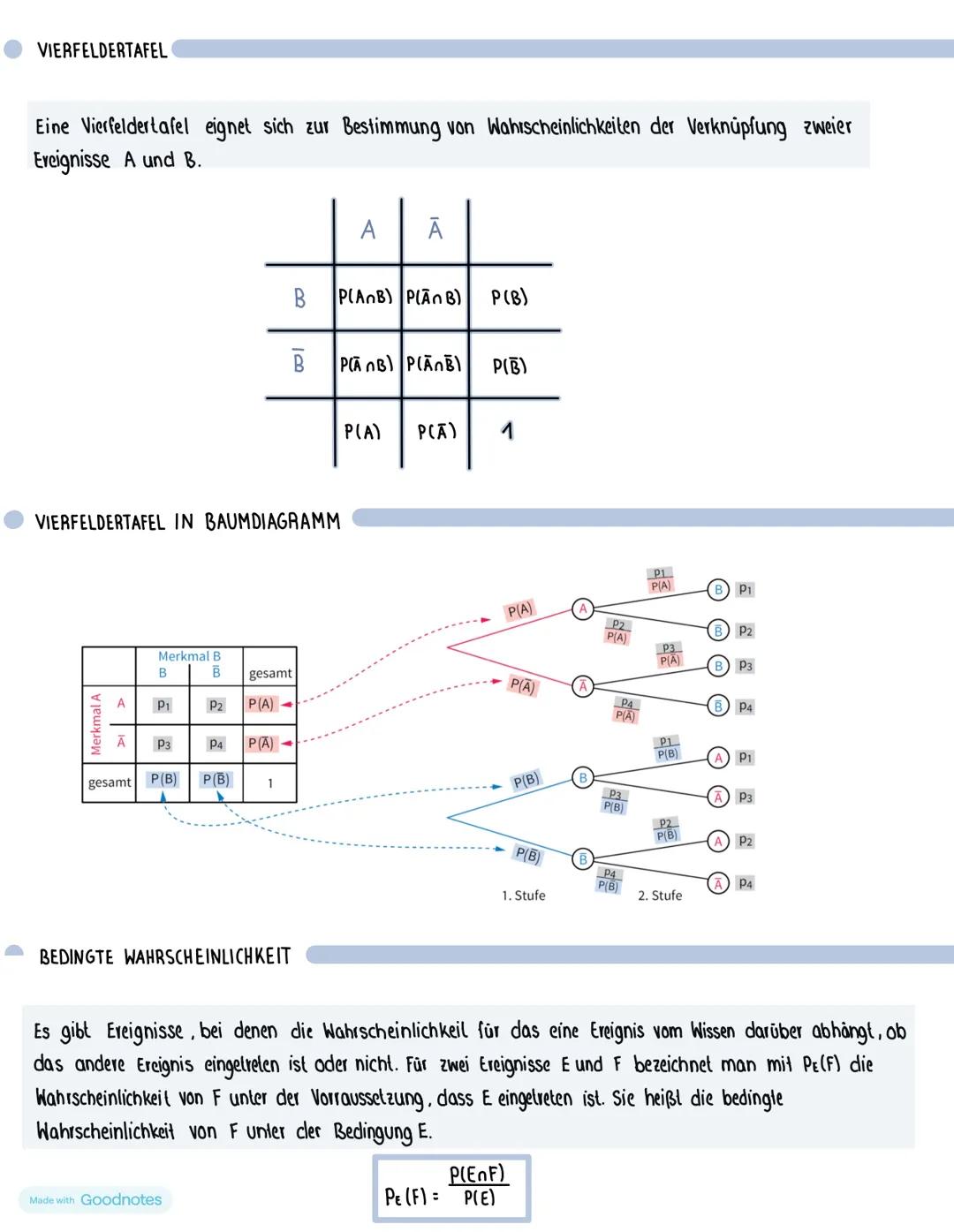
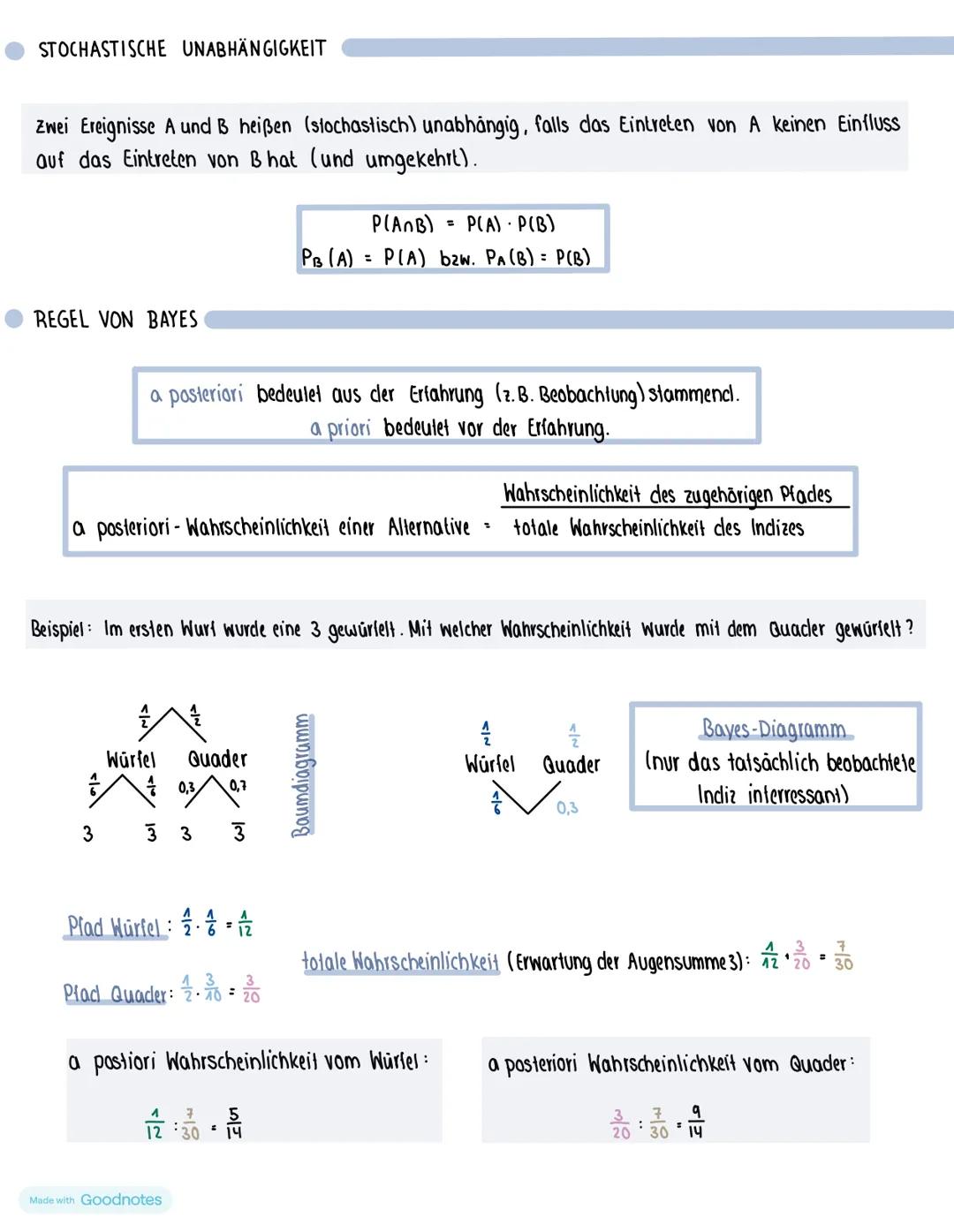
Der Signifikanztest prüft, ob deine Vermutung (Hypothese) über eine Wahrscheinlichkeit stimmt. Die Nullhypothese H₀ ist deine Behauptung, die du so lange glaubst, bis die Daten dagegen sprechen.

Das Signifikanzniveau α (meist 5%) ist deine maximale Irrtumswahrscheinlichkeit. Es gibt an, wie selten ein Ergebnis sein muss, damit du deine Hypothese verwirfst.

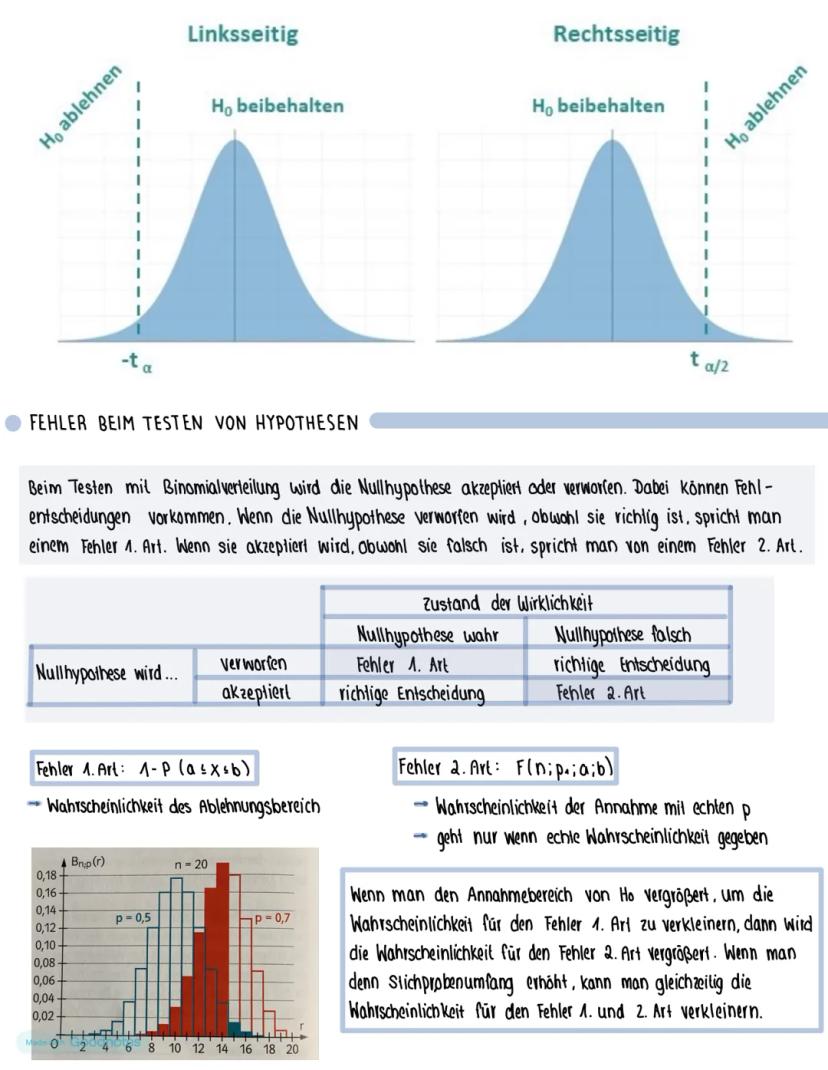
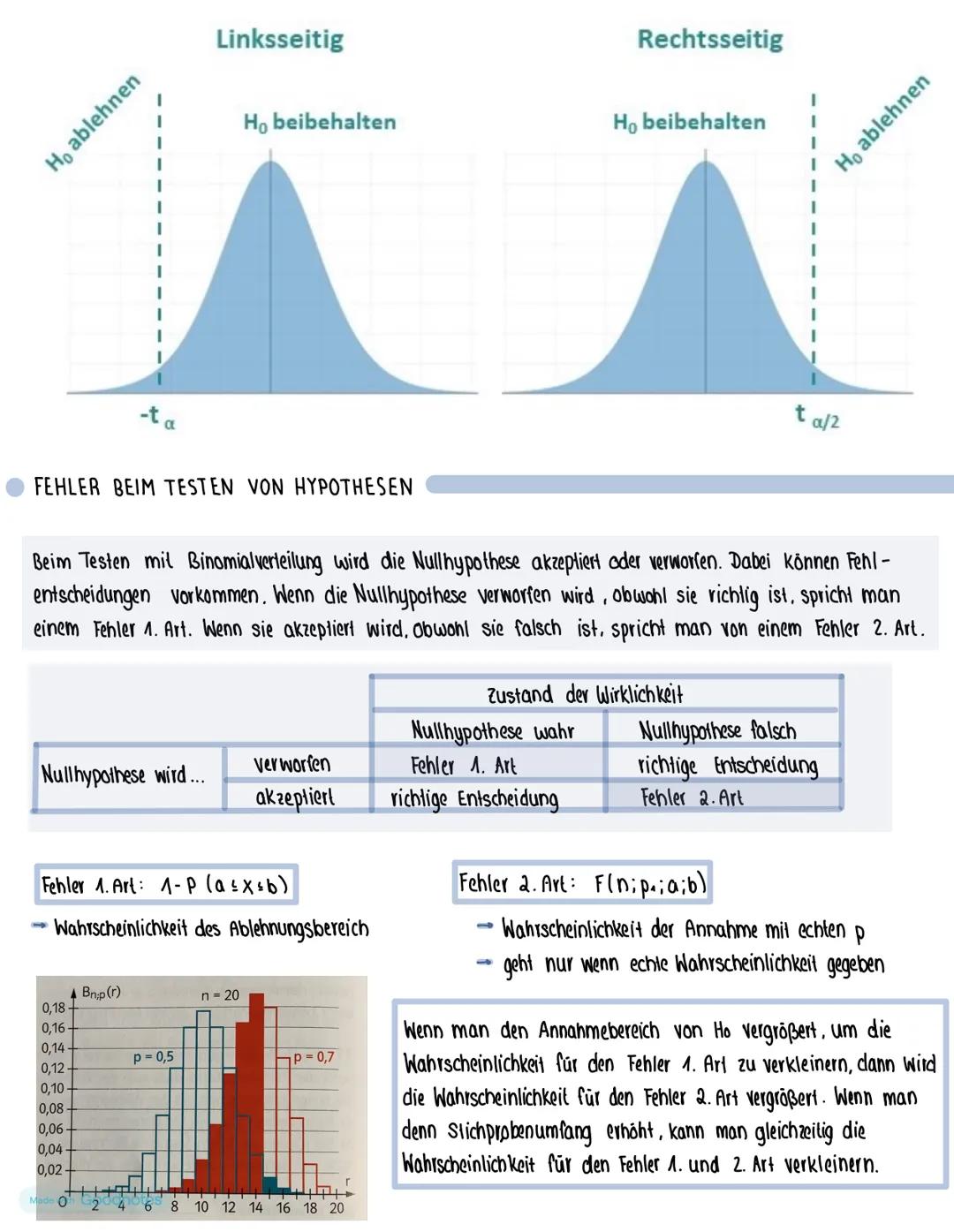
Beim zweiseitigen Test testest du H₀: p = p₀ gegen H₁: p ≠ p₀. Du erwartest eine Veränderung, weißt aber nicht in welche Richtung. Der Annahmebereich wird symmetrisch um den Erwartungswert gelegt.

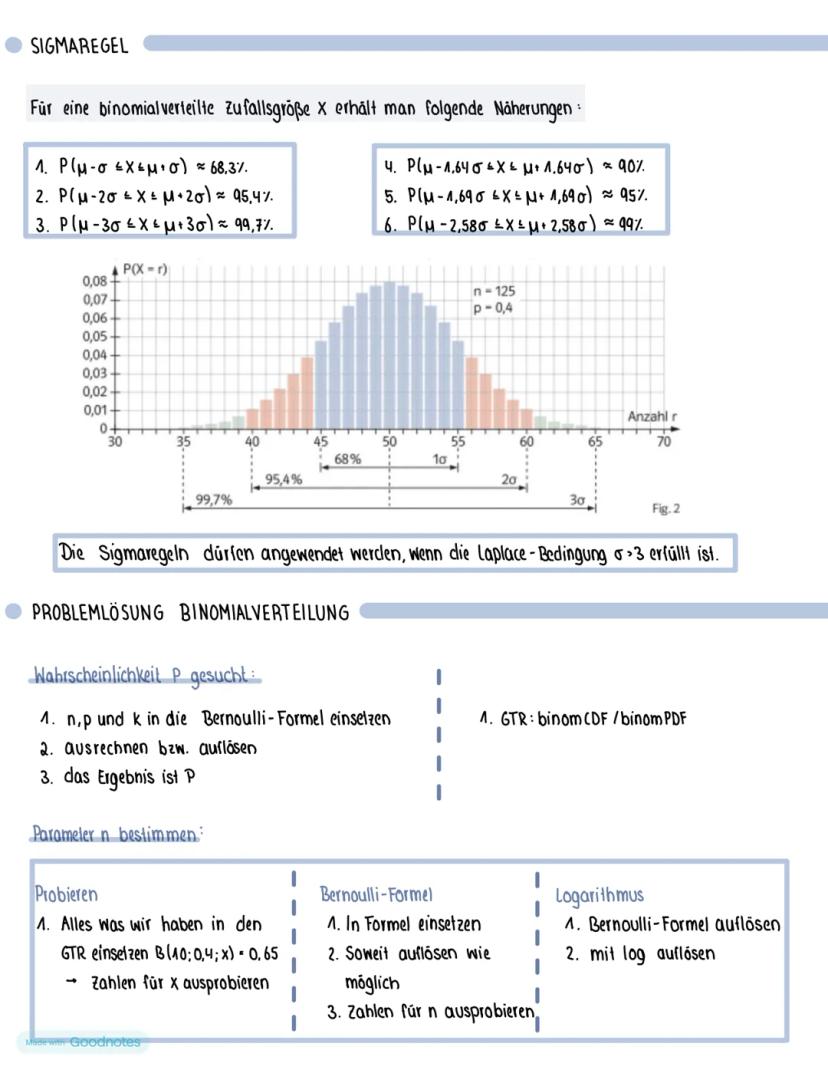
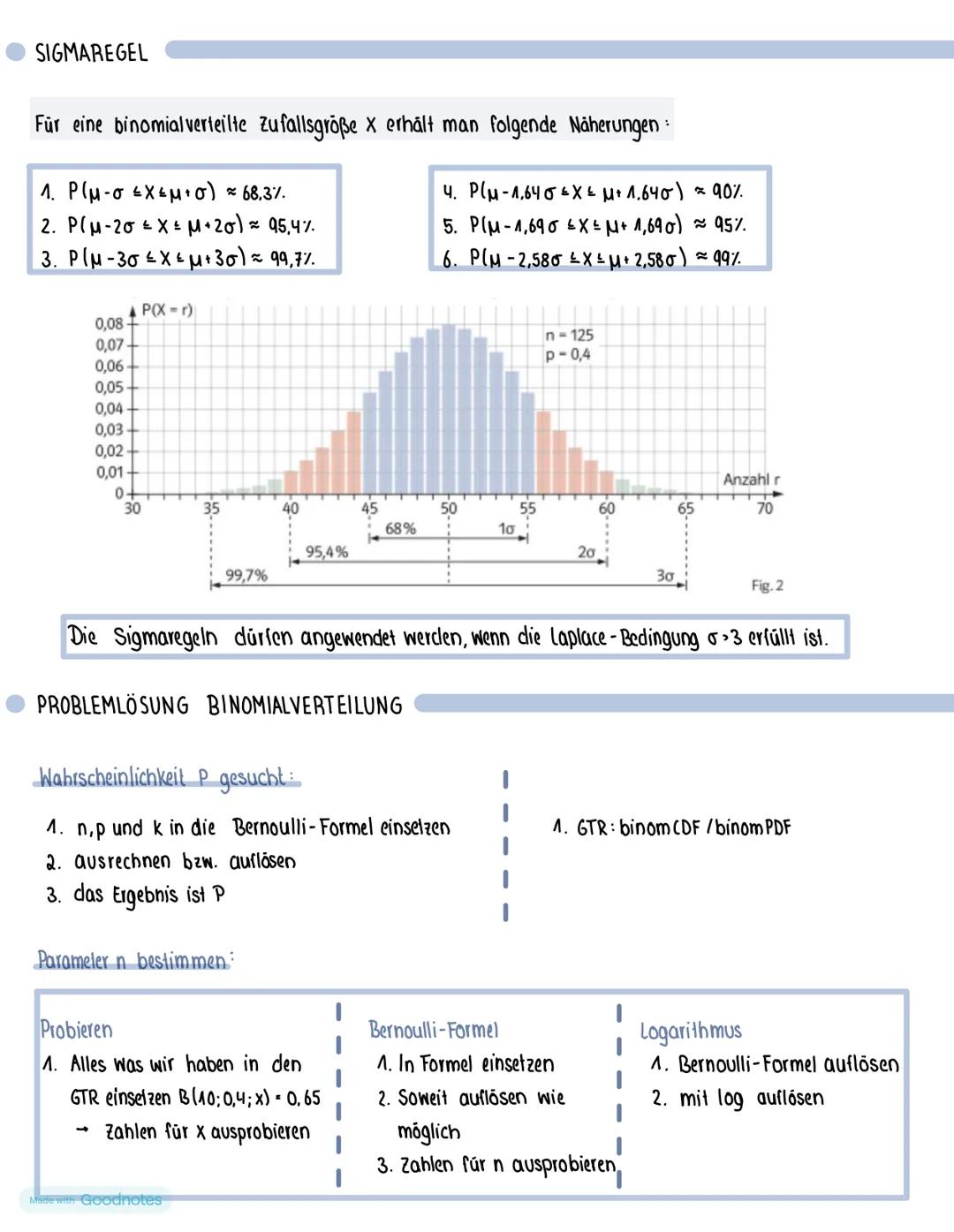
Annahmebereich bestimmen: Entweder mit Sigmaregeln (μ ± 1,96σ bei 5% Signifikanz) oder mit dem GTR (Wertetabelle, suche Werte zwischen 0,025 und 0,975).

💡 Merktipp: Signifikanztests sind wie Qualitätskontrolle - wenn das Ergebnis zu extrem ist, zweifelst du an deiner ursprünglichen Annahme!

Einseitige Signifikanztests

Einseitige Tests verwendest du, wenn du bereits weißt, in welche Richtung sich die Wahrscheinlichkeit verändert haben könnte. Das macht den Test schärfer und aussagekräftiger.

Linksseitiger Test: H₀: p ≥ p₀ gegen H₁: p < p₀. Du suchst die kleinste Zahl a mit P(X ≤ a) > 5%. Der Annahmebereich ist $a; n$.

Rechtsseitiger Test: H₀: p ≤ p₀ gegen H₁: p > p₀. Du suchst die größte Zahl b mit P(X ≤ b) > 95%. Der Annahmebereich ist $0; b$.

Die Entscheidung ist klar: Liegt dein Stichprobenergebnis im Annahmebereich, behältst du H₀ bei. Liegt es außerhalb, lehnst du H₀ ab und akzeptierst die Alternative.

💡 Merktipp: Einseitige Tests sind wie eine gerichtete Vermutung - du sagst nicht nur "es hat sich geändert", sondern "es ist besser/schlechter geworden"!

Fehler beim Testen

Beim Testen können zwei Arten von Fehlern auftreten: Fehler 1. Art (H₀ verwerfen, obwohl sie wahr ist) und Fehler 2. Art (H₀ akzeptieren, obwohl sie falsch ist).

Fehler 1. Art entspricht genau dem Signifikanzniveau α. Seine Wahrscheinlichkeit ist 1 - P(a ≤ X ≤ b), also die Wahrscheinlichkeit des Ablehnungsbereichs.

Fehler 2. Art kann nur berechnet werden, wenn die echte Wahrscheinlichkeit bekannt ist. Seine Wahrscheinlichkeit ist F(n; p₁; a; b) - die Wahrscheinlichkeit, dass bei der wahren Verteilung ein Wert im Annahmebereich landet.

Es besteht ein Zielkonflikt: Vergrößerst du den Annahmebereich (weniger Fehler 1. Art), steigt die Wahrscheinlichkeit für Fehler 2. Art. Nur durch größere Stichproben kannst du beide Fehlerarten gleichzeitig reduzieren.

💡 Merktipp: Denk an Brandmelder - zu empfindlich $viele Fehlalarme = Fehler 1. Art$, zu träge $Brand wird übersehen = Fehler 2. Art$!

Stetige Zufallsgrößen und Wahrscheinlichkeitsdichte

Stetige Zufallsgrößen haben unendlich viele mögliche Werte mit beliebig vielen Nachkommastellen - wie Körpergrößen oder Geschwindigkeiten. Hier werden Integrale statt Summen verwendet.

Die Wahrscheinlichkeitsdichte f(x) ist keine direkte Wahrscheinlichkeit, sondern eine Funktion, aus der du durch Integration Wahrscheinlichkeiten erhältst. Die Wahrscheinlichkeit für einen exakten Wert ist immer null.

Eigenschaften einer Wahrscheinlichkeitsdichte: f(x) ≥ 0 für alle x im Intervall und das Integral über das gesamte Intervall ergibt 1. So wird garantiert, dass alle Wahrscheinlichkeiten zwischen 0 und 1 liegen.

Erwartungswert μ = ∫ x · f(x) dx und Standardabweichung σ = √∫$x-μ$² · f(x) dx. Diese Formeln sind die kontinuierlichen Versionen der bekannten diskreten Formeln.

💡 Merktipp: Bei stetigen Größen fragst du nie "Wie wahrscheinlich ist genau 1,75432... m?", sondern immer "Wie wahrscheinlich ist zwischen 1,70 m und 1,80 m?"!