Grundlagen - Mathe Basics

Addition ist die Basis für alles weitere in der Mathematik. Mit 1+1=2 fängt alles an, aber keine Sorge - es wird gleich viel spannender!

Die einfachsten Rechenoperationen sind das Fundament für komplexere mathematische Konzepte. Du wirst sehen, dass sich auch schwierige Aufgaben oft auf diese Grundlagen zurückführen lassen.

Tipp: Auch bei komplexen Formeln gilt - Step by Step zum Ziel!

Geraden und quadratische Funktionen

Geradengleichungen bestimmst du mit der Formel $M = \frac{y_a - y_o}{x_a - x_o}$. Das ist einfach die Steigung zwischen zwei Punkten.

Bei quadratischen Funktionen startest du mit der Normalparabel $f(x) = x^2$. Die allgemeine Form ist $f(x) = a(x + d)^2 + e$, wobei jeder Parameter eine bestimmte Aufgabe hat.

Der Parameter a streckt oder staucht die Parabel: Bei $a > 1$ wird sie gestreckt, bei $0 < a < 1$gestaucht. Ist$a < 0$, öffnet sich die Parabel nach unten.

Parameter d verschiebt die Parabel horizontal, Parameter e vertikal. Der Scheitelpunkt liegt dann bei $S(d|e)$.

Merkhilfe: d = horizontal, e = vertikal - wie bei Koordinaten!

Umrechnung zwischen Formen

Du kannst zwischen Scheitelform und Normalform hin und her wechseln. Von Scheitel- zur Normalform rechnest du einfach aus.

Für die andere Richtung brauchst du die quadratische Ergänzung. Bei $f(x) = x^2 + 6x + 13$ ergänzt du zum Binom: $(x+3)^2 = x^2 + 6x + 9$.

Das funktioniert so: Du nimmst die Hälfte des mittleren Koeffizienten $hier 6÷2=3$ und quadrierst sie. Dann addierst und subtrahierst du diesen Wert wieder.

Bei Vorfaktoren klammerst du zuerst aus: $2x^2 + 16x + 41 = 2$x^2 + 8x$ + 41$. Dann machst du die quadratische Ergänzung und ziehst das Doppelte des ergänzten Wertes ab.

Trick: Immer dran denken - was du hinzufügst, musst du auch wieder abziehen!

Parameter und Diskriminante

Mit der Diskriminante $p^2 - 4q$ erkennst du, wie viele Schnittpunkte eine Parabel mit einer Geraden hat.

Bei Diskriminante > 0 gibt es zwei Lösungen (Sekante). Bei Diskriminante = 0 eine Lösung (Tangente). Bei Diskriminante < 0 keine Lösung (Passante).

Potenzfunktionen haben die Form $f(x) = x^n$. Sie beschreiben zum Beispiel die Kantenlänge $K(x) = 4x$, Oberfläche $O(x) = 6x^2$ oder das Volumen $V(x) = x^3$ eines Würfels.

Die Lösungsformel $x_{1,2} = \frac{-p \pm \sqrt{p^2 - 4q}}{2}$ hilft dir bei allen quadratischen Gleichungen.

Eselsbrücke: Sekante schneidet zweimal, Tangente berührt einmal, Passante geht vorbei!

Eigenschaften von Funktionen

Symmetrie checkst du rechnerisch: Bei Achsensymmetrie gilt $f(x) = f(-x)$ (nur gerade Exponenten). Bei Punktsymmetrie gilt $f(-x) = -f(x)$ (nur ungerade Exponenten).

Das Steigungsverhalten erkennst du am Graphen: Funktionen können monoton steigend, fallend oder abschnittsweise unterschiedlich verlaufen.

Beim Verhalten im Unendlichen schaust du auf den höchsten Exponenten und seinen Vorfaktor. Bei $f(x) = x^4 - 3x^3 + x^2 + 1$ dominiert das $x^4$, also geht $f(x) → ∞$ für $x → ±∞$.

Eine Wertetabelle hilft dir, das Verhalten zu verstehen und zu visualisieren.

Tipp: Der höchste Exponent bestimmt das Verhalten im Unendlichen - alles andere wird unwichtig!

Nullstellen berechnen

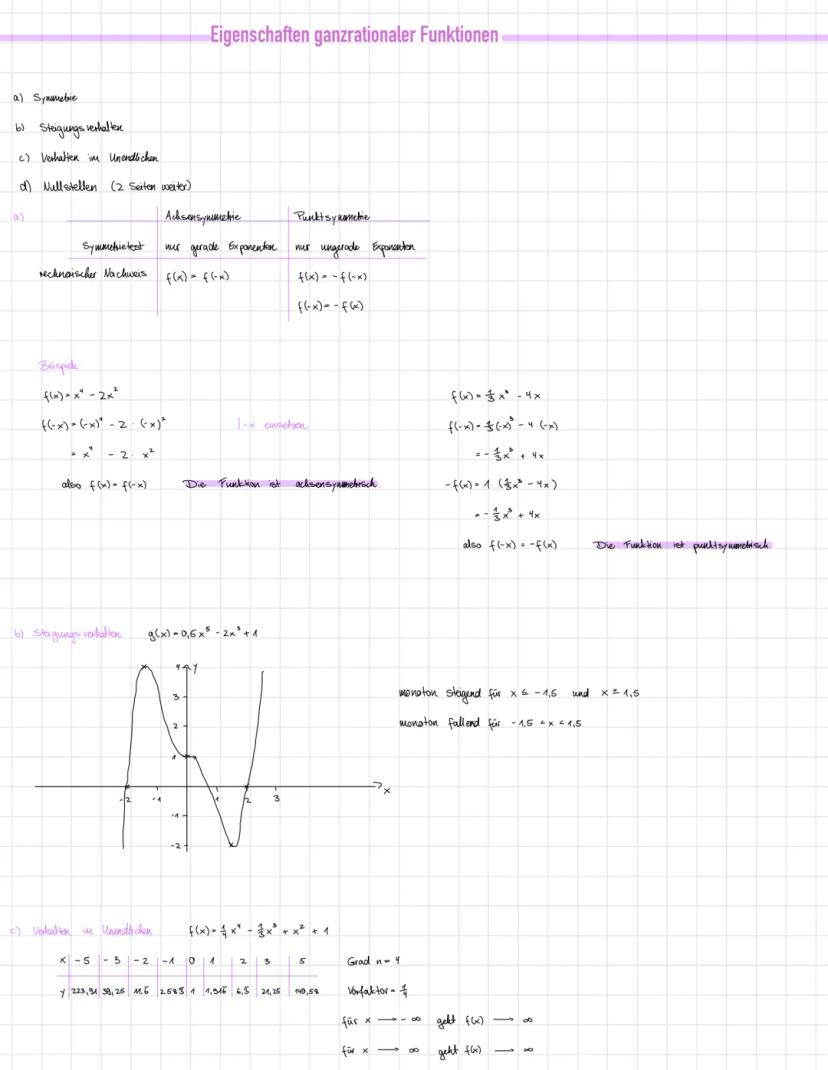
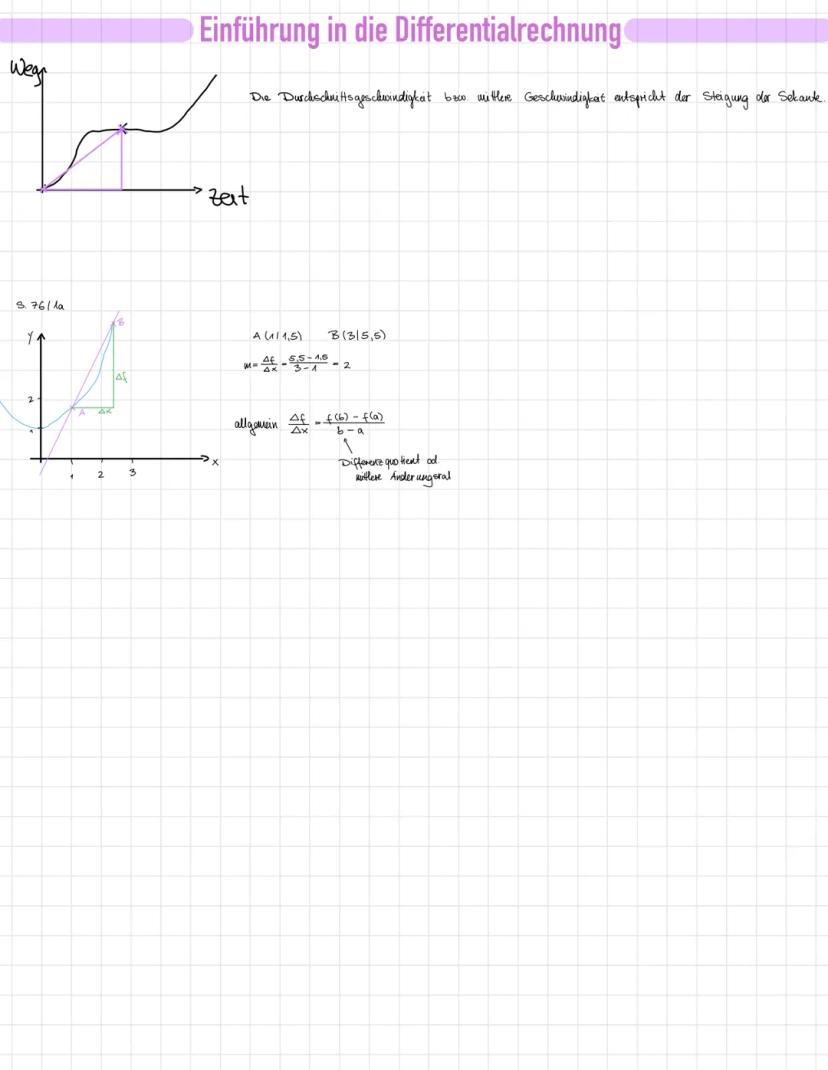
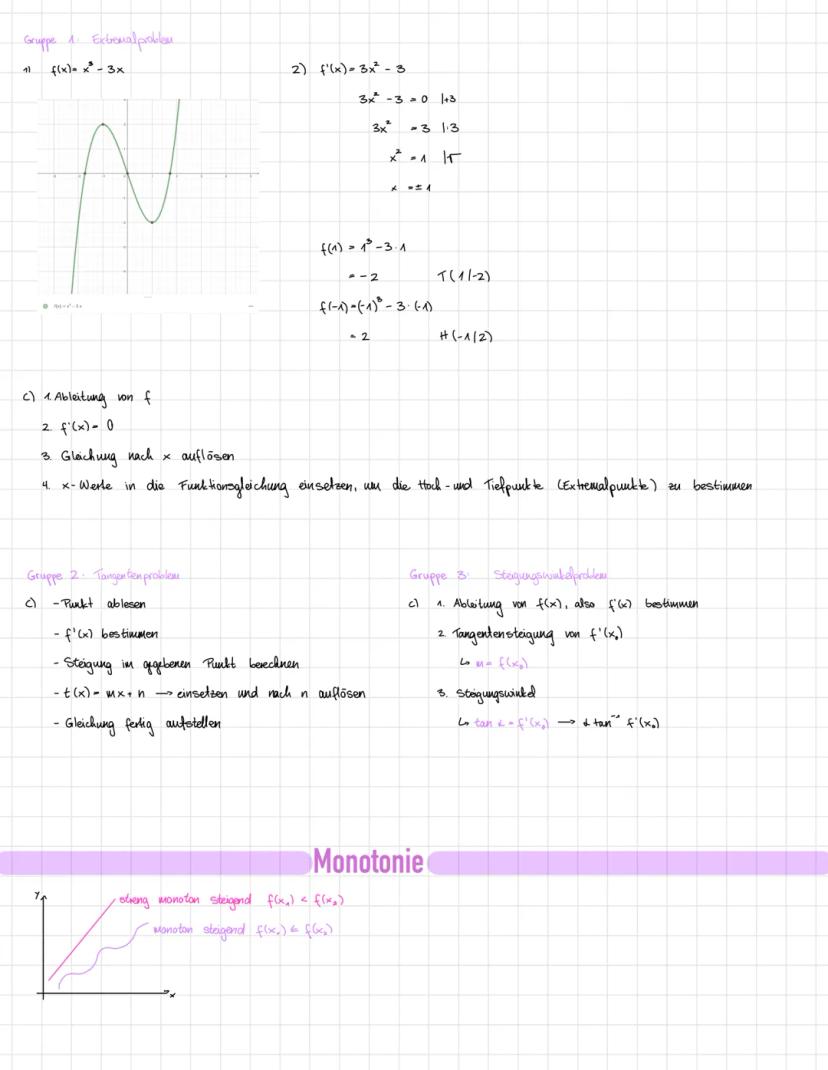
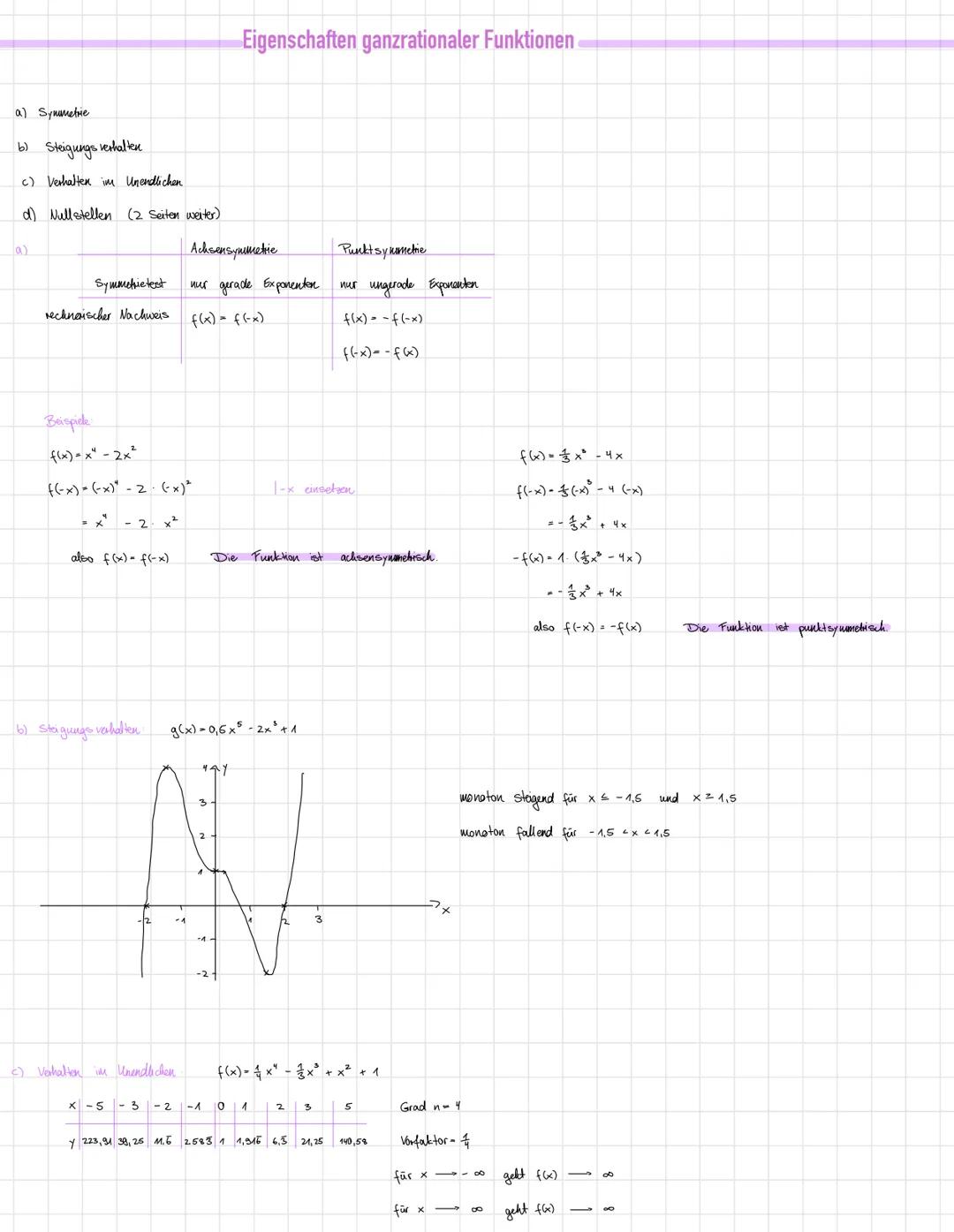
Nullstellen findest du, indem du $f(x) = 0$ setzt. Bei $f(x) = x^3 - 2x^2 - 8x$ klammerst du zuerst $x$ aus: $x(x^2 - 2x - 8) = 0$.

Ein Produkt ist null, wenn einer der Faktoren null ist. Also ist $x = 0$ eine Lösung, und für $x^2 - 2x - 8 = 0$ verwendest du die Lösungsformel.

Bei biquadratischen Gleichungen wie $x^4 - 7x^2 + 12 = 0$ substitutierst du $u = x^2$. Dann löst du $u^2 - 7u + 12 = 0$ und setzt die Lösungen wieder ein.

Die Linearfaktordarstellung zeigt alle Nullstellen auf einen Blick: $x(x-4)(x+2)$ hat die Nullstellen $x = 0, 4, -2$.

Strategie: Ausklammern → Lösungsformel → Resubstitution. So knackst du jede Gleichung!

Einführung Differentialrechnung

Die Durchschnittsgeschwindigkeit entspricht der Steigung der Sekante zwischen zwei Punkten. Mit $A(1|1,5)$ und $B(3|5,5)$ berechnest du: $m = \frac{5,5-1,5}{3-1} = \frac{4}{2} = 2$.

Der Differenzquotient $\frac{\Delta f}{\Delta x} = \frac{f(b)-f(a)}{b-a}$ gibt dir die mittlere Änderungsrate zwischen zwei Stellen.

Das ist der erste Schritt zur Ableitung - später wird daraus die momentane Änderungsrate.

Durchblick: Die Sekante wird später zur Tangente - das ist der Kern der Differentialrechnung!

Ableitungsregeln

Die wichtigsten Ableitungsregeln musst du auswendig können:

Potenzregel: $f(x) = x^n → f'(x) = n \cdot x^{n-1}$. Faktorregel: $f(x) = a \cdot x^n → f'(x) = n \cdot a \cdot x^{n-1}$. Konstantenregel: $f(x) = a → f'(x) = 0$.

Die Summenregel besagt: $(g(x) + h(x))' = g'(x) + h'(x)$. Du leitest jeden Summanden einzeln ab.

Beispiel: $f(x) = 4x^2 + 2x → f'(x) = 8x + 2$.

Diese Regeln funktionieren immer und machen Ableitungen zum Kinderspiel, sobald du sie drauf hast.

Power-Tipp: Exponent nach vorn, dann um eins reduzieren - fertig ist die Ableitung!

Steigungsverhalten und Tangenten

Mit der Ableitung bestimmst du das Steigungsverhalten: $f'(x) > 0$ bedeutet steigend, $f'(x) < 0$ fallend, $f'(x) = 0$ waagerecht.

Für eine bestimmte Steigung setzt du $f'(x) = M$ und löst nach $x$ auf. Bei $f'(x) = 1,2x^2 - 6x + 5 = 4$ findest du die Stellen mit Steigung 4.

Das Normalenproblem: Normale und Tangente stehen senkrecht aufeinander, also gilt $m_t \cdot m_n = -1$.

Bei $f(x) = \sqrt{x}$ ist $f'(x) = \frac{1}{2\sqrt{x}}$ - auch Wurzelfunktionen kannst du ableiten!

Merksatz: Tangente und Normale sind Feinde - ihr Steigungsprodukt ist immer -1!