Praktische Anwendung: Sekantensteigung berechnen
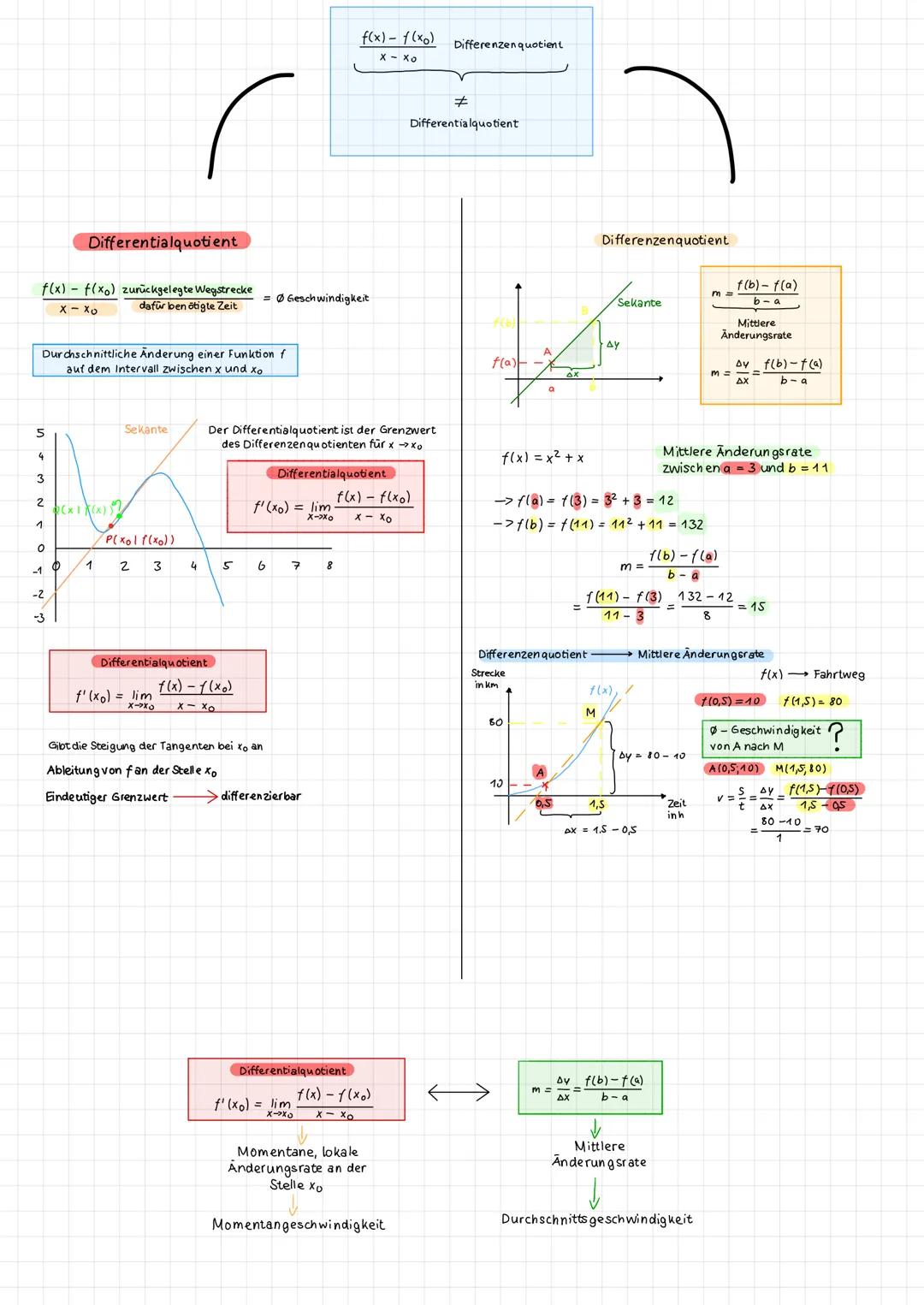
Die mittlere Änderungsrate zwischen zwei Punkten könnt ihr mit der Formel b−af(b)−f(a) berechnen. Diese Sekante verbindet zwei Punkte auf der Funktion und zeigt deren Steigung.
Ein Beispiel macht's klar: Bei den Punkten (0,5∣2) und (2∣3) ergibt sich eine Steigung von 2−0,53−1,125=1,25. Die Sekantengleichung lautet dann y=1,25x+0,5.
Den Steigungswinkel bekommt ihr über den Arkustangens: φ=arctan(1,25)≈51°. So könnt ihr visualisieren, wie steil die Sekante tatsächlich ist.
Praxistipp: Je näher die beiden Punkte beieinander liegen, desto genauer nähert sich die Sekantensteigung der tatsächlichen Tangentensteigung an.
Mit verschiedenen Punktpaaren seht ihr, wie sich die Steigung verändert - das ist der erste Schritt zum Verständnis der Ableitung!