Loslegen

Mathematik

Ableitungen und Anwendungen

Differenzenquotient

Mathe1.111Aktualisiert 6. Sept. 20265 Seiten

Einführung in Differenzenquotienten und Ableitungen

Melden
user profile picture
Lilly@lillyrose_89099
Zu Google-Quellen hinzufügen
Steigungen von Funktionen verstehen ist entscheidend für die Analysis. Du lernst hier den Unterschied zwischen durchschnittlicher und momentaner Änderung kennen - das ist die Basis für alles, was in der Differentialrechnung folgt.
Analysis – Seite 1

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

  • Zugriff auf alle Dokumente
  • Verbessere deine Noten
  • Schließ dich Millionen Schülern an

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und Datenschutzerklärung

Differenzenquotient und mittlere Änderungsrate

Der Differenzenquotient zeigt dir, wie steil eine Funktion zwischen zwei Punkten ansteigt oder fällt. Du berechnest einfach die Steigung der Sekante zwischen diesen Punkten.

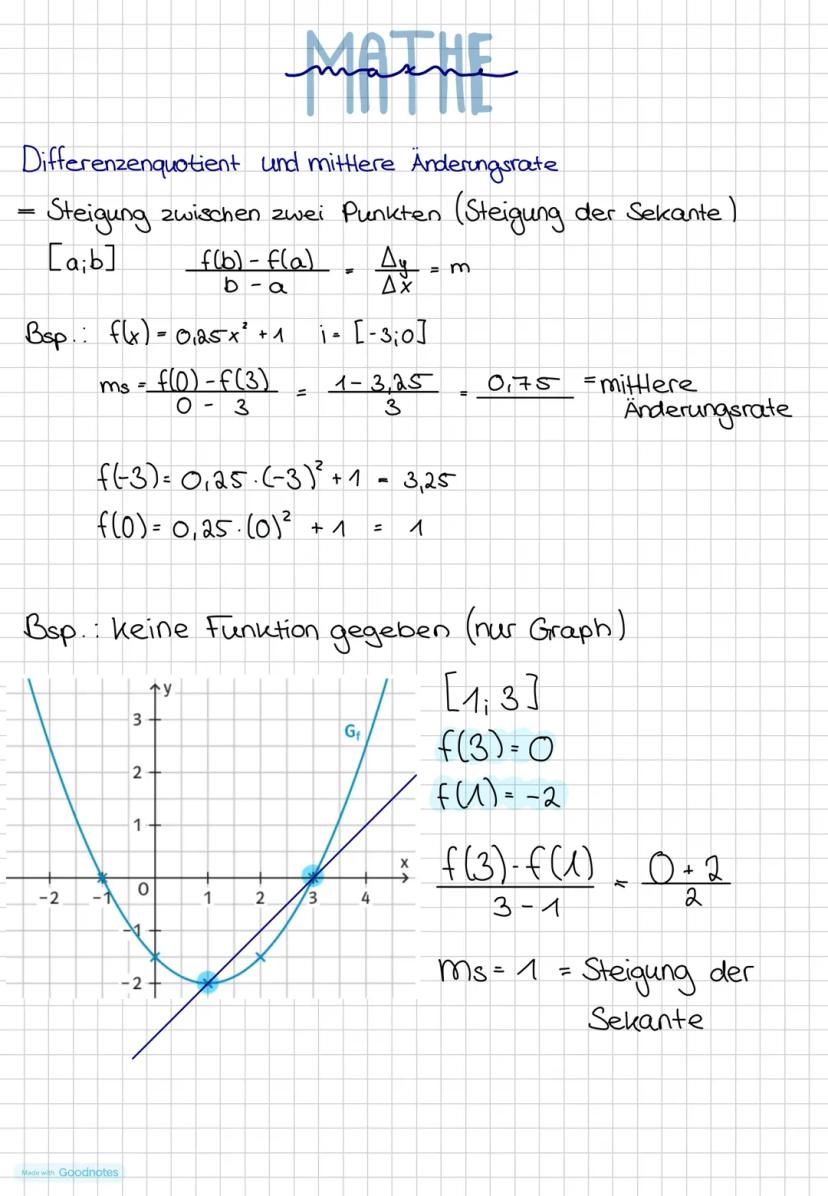
Die Formel ist super simpel: f(b)−f(a)b−a\frac{f(b) - f(a)}{b - a}. Das kennst du schon von der Geradensteigung als ΔyΔx\frac{\Delta y}{\Delta x}.

Bei fxx = 0,25x² + 1 im Intervall −3;0-3;0 rechnest du: f−3-3 = 3,25 und f(0) = 1. Also: 1−3,250−(−3)=−0,75\frac{1 - 3,25}{0 - (-3)} = -0,75. Die Funktion fällt also durchschnittlich um 0,75 pro Einheit.

💡 Merktipp: Der Differenzenquotient ist wie die Durchschnittsgeschwindigkeit - er zeigt die mittlere Veränderung über eine Strecke.

Analysis – Seite 2

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

  • Zugriff auf alle Dokumente
  • Verbessere deine Noten
  • Schließ dich Millionen Schülern an

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und Datenschutzerklärung

Differentialquotient und Ableitung

Während der Differenzenquotient die durchschnittliche Änderung misst, zeigt der Differentialquotient die momentane Änderung an einem einzigen Punkt. Das ist die Steigung der Tangente.

Die Formel sieht kompliziert aus: lim⁡h→0f(x0+h)−f(x0)h\lim_{h \to 0} \frac{f(x_0+h)-f(x_0)}{h}. Aber keine Sorge - du machst h immer kleiner, bis du die exakte Steigung hast.

Praktisch nutzt du einfach die Ableitungsregeln: Aus fxx = 0,25x² + 1 wird f'xx = 0,5x. An der Stelle x = 3 ist die Steigung f'(3) = 1,5.

🎯 Klausurtipp: Die Ableitung ist dein Werkzeug für Tangentensteigungen - lerne die Ableitungsregeln auswendig!

Analysis – Seite 3

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

  • Zugriff auf alle Dokumente
  • Verbessere deine Noten
  • Schließ dich Millionen Schülern an

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und Datenschutzerklärung

Differenzierbarkeit

Eine Funktion ist nicht differenzierbar, wenn sie einen Knick hat. Das erkennst du daran, dass die linksseitige und rechtsseitige Steigung unterschiedlich sind.

Bei stückweise definierten Funktionen prüfst du die Übergangsstelle besonders genau. Wenn die Grenzwerte von links und rechts verschiedene Werte haben, gibt es einen Knick.

Im Beispiel mit der Funktion, die bei x = 4 den Übergang hat, erhältst du linksseitig die Steigung 2 und rechtsseitig die Steigung 1. Da 2 ≠ 1, ist die Funktion nicht differenzierbar.

⚠️ Achtung: Auch wenn eine Funktion stetig ist, kann sie trotzdem einen Knick haben und damit nicht differenzierbar sein!

Analysis – Seite 4

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

  • Zugriff auf alle Dokumente
  • Verbessere deine Noten
  • Schließ dich Millionen Schülern an

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und Datenschutzerklärung

Tangentengleichung und Normale

Mit der Tangentengleichung findest du die Gerade, die eine Funktion an einem bestimmten Punkt berührt. Du brauchst nur die Steigung f'(x₀) und den Berührpunkt.

Die Formel y = mx + t kennst du schon. Bei fxx = x³ am Punkt (2|8) ist m = f'(2) = 12. Einsetzen ergibt: 8 = 12·2 + t, also t = -16. Die Tangentengleichung lautet y = 12x - 16.

Die Normale steht senkrecht zur Tangente. Ihre Steigung ist der negative Kehrwert: m₂ = -1/12. Mit dem gleichen Punkt erhältst du die Normalengleichung.

📐 Eselsbrücke: Tangente = berührt, Normale = steht senkrecht drauf. Steigungen multipliziert ergeben -1.

Analysis – Seite 5

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

  • Zugriff auf alle Dokumente
  • Verbessere deine Noten
  • Schließ dich Millionen Schülern an

Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und Datenschutzerklärung

Steigungswinkel und Ableitungsfunktion

Den Steigungswinkel berechnest du mit tan α = m. Bei einer Steigung von 12 ist α ≈ 85,24° - ziemlich steil!

Die Ableitungsfunktion f' zeigt dir zu jedem x-Wert die momentane Steigung. Aus fxx = x⁴ wird f'xx = 4x³, aus gxx = x³ wird g'xx = 3x².

Beim Zuordnen von Graphen achte auf die Eigenschaften: f'xx = 4x³ ist eine kubische Funktion (Graph 3. Grades), g'xx = 3x² ist eine nach oben geöffnete Parabel.

🔍 Analysehilfe: Wo die ursprüngliche Funktion steigt, ist die Ableitung positiv. Wo sie fällt, ist die Ableitung negativ.

Wir dachten schon, du fragst nie...

Unser KI-Begleiter ist ein speziell für Schüler entwickeltes KI-Tool, das mehr als nur Antworten bietet. Basierend auf Millionen von Knowunity-Inhalten liefert er relevante Informationen, personalisierte Lernpläne, Quizze und Inhalte direkt im Chat und passt sich deinem individuellen Lernweg an.

Du kannst die App im Google Play Store und im Apple App Store herunterladen.

Genau! Genieße kostenlosen Zugang zu Lerninhalten, vernetze dich mit anderen Schülern und hol dir sofortige Hilfe – alles direkt auf deinem Handy.

Ähnlicher Inhalt

Mathe

Differenzenquotient Berechnung

Erfahren Sie, wie der Differenzenquotient zur Berechnung der Steigung einer Funktion verwendet wird. Diese Zusammenfassung bietet eine klare Erklärung des Konzepts, eine anschauliche Skizze und eine Schritt-für-Schritt-Beispielrechnung zur Veranschaulichung der Anwendung. Ideal für Studierende, die die Grundlagen der Differentialrechnung verstehen möchten.

103.057164
Mathe

Differenzen- und Differentialquotient

Erfahren Sie alles über den Differenzenquotienten und Differentialquotienten, einschließlich der Steigung von Tangenten und Sekanten, der mittleren Änderungsrate und der momentanen Geschwindigkeit. Diese Zusammenfassung bietet klare Erklärungen und Beispiele zur Anwendung dieser Konzepte in der Mathematik.

122.227119
Mathe

Differenzenquotient und Ableitungen

Diese Zusammenfassung behandelt den Differenzenquotienten, die Ableitung und die mittlere Änderungsrate einer Funktion. Erfahren Sie, wie man die Sekantensteigung berechnet und die momentane Änderungsrate an einem Punkt bestimmt. Ideal für Studierende der Mathematik, die sich auf Differentialrechnung vorbereiten. Typ: Zusammenfassung.

101.24621
Mathe

Ableitungen & Änderungsraten

Diese Zusammenfassung behandelt die Konzepte der Ableitungen, der mittleren Änderungsrate und des Differenzenquotienten. Sie ist ideal für Schüler, die sich auf ihre Matheklausur vorbereiten und ein besseres Verständnis für Differentialrechnung entwickeln möchten. Enthält Beispiele und Berechnungen zur Anwendung dieser Konzepte in verschiedenen Intervallen.

106.564313
Mathe

Differentialquotienten & Asymptoten

Diese Zusammenfassung behandelt die Konzepte des Differentialquotienten, der lokalen und globalen Änderungsraten sowie gebrochen rationaler Funktionen. Erfahren Sie, wie man Ableitungen bestimmt, das Verhalten im Unendlichen analysiert und Asymptoten identifiziert. Ideal für Studierende der Mathematik, die sich auf Prüfungen vorbereiten oder ihr Verständnis vertiefen möchten.

91.00727
Mathe

Änderungsraten und Tangenten

Erfahre alles über die mittlere und lokale Änderungsrate in der Mathematik. Diese Zusammenfassung behandelt den Differenzenquotienten, die Ableitungsfunktion, die Steigung der Tangente sowie die Aufstellung der Tangentengleichung. Ideal für die Vorbereitung auf Matheprüfungen und das Verständnis von Funktionen und deren Verhalten.

105865
Mehr anzeigen

Beliebtester Inhalt: Differenzenquotient

Mathe

Differenzenquotient und Ableitungen

Entdecken Sie die Konzepte des Differenzenquotienten und der Ableitungen in der Mathematik. Diese Zusammenfassung behandelt die Berechnung von Steigungen, Tangenten und Normalen sowie die Anwendung der Differenzierungsregeln. Ideal für Studierende im Grundkurs Mathematik, die ein tieferes Verständnis für lokale Änderungsraten und asymptotisches Verhalten entwickeln möchten.

1012.838368
Mathe

Berechnung der Änderungsrate

Erfahren Sie, wie man die mittlere Änderungsrate einer Funktion berechnet, indem Sie den Differenzenquotienten verwenden. Diese Zusammenfassung behandelt die Schritte zur Berechnung der Steigung der Sekante zwischen zwei Punkten auf einem Graphen, einschließlich der Anwendung der Formel m = (f(b) - f(a)) / (b - a). Ideal für Schüler, die sich auf Mathematikprüfungen vorbereiten. Typ: Zusammenfassung.

119.125217
Mathe

Lenzettel Mathe EF mit Klausur

Grenzwertverhalten ganzrationaler Funktionen, Elementarsymmetrie, Symmetrie, Nullstellen ganzrationaler Funktionen, Differentialrechnung, Momentane Änderungsrate, Ableitung, Binomische Formeln, Aufgabemöglichkeiten

111453
Mathe

Differenzen- und Differentialquotient

Dieses Lernblatt behandelt die Konzepte des Differenzenquotienten und Differentialquotienten in der Differentialrechnung. Es erklärt die durchschnittliche Änderungsrate und die momentane Änderungsrate einer Funktion sowie deren geometrische Bedeutung. Ideal für Studierende, die ein tieferes Verständnis für die Steigung von Sekanten und Tangenten entwickeln möchten.

102.89160
Mathe

Differentialquotient & Tangente

Erforschen Sie die Konzepte des Differentialquotienten, der mittleren und lokalen Änderungsrate sowie der Differenzierbarkeit. Diese Zusammenfassung behandelt die h-Methode zur Ableitung und die Gleichungen für Tangente und Normale an Funktionen. Ideal für Studierende der Mathematik, die ein tieferes Verständnis der Differentialrechnung suchen.

114568
Mathe

Differenzenquotient & Änderungsrate

Erfahren Sie, wie man die mittlere Änderungsrate und den Differenzenquotienten berechnet. Diese Zusammenfassung bietet eine klare Erklärung der Konzepte, Beispiele zur Anwendung und eine Schritt-für-Schritt-Anleitung zur Berechnung der Steigung zwischen zwei Punkten auf einem Graphen. Ideal für Schüler, die sich auf Mathematikprüfungen vorbereiten.

112.46368
Mathe

Differenzenquotient Berechnung

Erfahren Sie, wie der Differenzenquotient zur Berechnung der Steigung einer Funktion verwendet wird. Diese Zusammenfassung bietet eine klare Erklärung des Konzepts, eine anschauliche Skizze und eine Schritt-für-Schritt-Beispielrechnung zur Veranschaulichung der Anwendung. Ideal für Studierende, die die Grundlagen der Differentialrechnung verstehen möchten.

103.057164
Mathe

Differenzenquotient und Ableitungen

Diese Zusammenfassung behandelt den Differenzenquotienten, die Ableitung und die mittlere Änderungsrate einer Funktion. Erfahren Sie, wie man die Sekantensteigung berechnet und die momentane Änderungsrate an einem Punkt bestimmt. Ideal für Studierende der Mathematik, die sich auf Differentialrechnung vorbereiten. Typ: Zusammenfassung.

101.24621
Mathe

Differenzen- und Differentialquotient

Erfahren Sie alles über den Differenzenquotienten und den Differentialquotienten. Dieser Leitfaden behandelt die Definitionen, die Berechnung der Steigung der Sekante und Tangente sowie die durchschnittliche und momentane Änderungsrate. Ideal für Studierende der Differential- und Integralrechnung.

1093125

Beliebtester Inhalt: Mathe

Mathe

Quantitative Probleme im TMS

Entdecken Sie Strategien zur Lösung quantitativer und formaler Probleme im Medizinertest. Dieser Leitfaden umfasst wichtige Formeln zur Prozentrechnung, Umrechnungen von Einheiten und die Eigenschaften von Lösungen. Ideal für Studierende, die sich auf den Medizinertest vorbereiten und ihre mathematischen Fähigkeiten verbessern möchten.

1120.311597
Mathe

Integralrechnung und Flächenberechnung

Erfahre alles über die Integralrechnung, einschließlich unbestimmter und bestimmter Integrale, Integralschreibweise und Rechenregeln. Lerne, wie man Flächeninhalte zwischen Funktionsgraphen berechnet und die Kurvendiskussion durchführt. Ideal für die Vorbereitung auf Klausuren in der Differential- und Integralrechnung.

1213.435341
Mathe

Stochastik Lernzettel Abitur

Übersicht zu allen Stochastik Themen für das Mathe Abitur (Bayern 2026), Hypothesentest fehlt

111.49833
Mathe

Geraden und Ebenen im Raum

Entdecken Sie die Grundlagen der analytischen Geometrie mit Fokus auf Vektoren, Geraden und Ebenen. Erfahren Sie mehr über Lagebeziehungen, Abstände, Winkel und Orthogonalität. Ideal für Studierende der Mathematik und Ingenieurwissenschaften. Diese Zusammenfassung bietet klare Erklärungen und Beispiele zur Vertiefung des Verständnisses.

113.86096
Mathe

Analytische Geometrie Zusammenfassung

Umfassende Zusammenfassung der analytischen Geometrie für das Abitur. Behandelt wichtige Themen wie Abstandsberechnung, Lagebeziehungen von Geraden und Ebenen, Vektoroperationen, und geometrische Eigenschaften. Ideal für die Prüfungsvorbereitung.

118.321232
Mathe

Binomische Formeln verstehen

Entdecke die drei Binomischen Formeln mit detaillierten Erklärungen und Beispielen. Lerne, wie man sie anwendet, um algebraische Ausdrücke zu vereinfachen und zu lösen. Ideal für Schüler, die ihre Kenntnisse in Algebra vertiefen möchten.

720.9592.117
Mathe

Integrationsregeln und Anwendungen

Entdecken Sie die grundlegenden Rechenregeln für unbestimmte und bestimmte Integrale, einschließlich der Potenzregel, Summenregel und Substitutionsregel. Lernen Sie, wie man Stammfunktionen findet und die Fläche unter Graphen mit bestimmten Integralen berechnet. Ideal für Studierende der Mathematik und Ingenieurwissenschaften.

1141.2642.211
Mathe

Lineare Funktionen verstehen

Dieser Lernzettel bietet eine umfassende Übersicht über lineare Funktionen, einschließlich der allgemeinen Formel, der Bestimmung von Funktionsgleichungen, der Steigung und der Nullstellen. Ideal für Schüler, die sich auf Prüfungen vorbereiten oder ihr Verständnis vertiefen möchten. Enthält Beispiele und Schritt-für-Schritt-Anleitungen zur Berechnung von Schnittpunkten und zur Analyse von Graphen.

1116.787281
Mathe

Analysis: Funktionsscharen & Ableitungen

Dieser Lernzettel bietet eine umfassende Übersicht über zentrale Themen der Analysis, einschließlich Funktionsscharen, Ableitungen, Extrempunkte, Integrale und e-Funktionen. Ideal für die Vorbereitung auf das Abitur im Mathematik Grundkurs. Verstehe die Konzepte und deren Anwendungen mit klaren Beispielen und Schritt-für-Schritt-Anleitungen.

1113.807294

Beliebtester Inhalt

Deutsch

Heimsuchung Abitur 2026 Lernzettel

Alles über Heimsuchung, Kapitelzusaemfassung, Themen, Deutung, Figurenkonstellation und mögliche Streitfragen

129.673230
Deutsch

Heimsuchung_JennyErpenbeck_Abitur

Zusammenfassungen für jedes Kapitel, Analysen und Zitate

1218.717360
Deutsch

Abilernzettel Heimsuchung 2025

Figurenkonstellation, Kapitel Zusammenfassung, Charaktere, Motive, Deutungsansätze,

1151.1981.050
Deutsch

Heimsuchung komplette Zusammenfassung

Zusammenfassung des Buches als auch der einzelnen Kapitel und deren Charakteren. Auch tabellarisch. Im Unterricht ohne KI erstellt

129.168201
Lerntipps

Fahrschule Theorieprüfung Essentials

Entdecke die wichtigsten Punkte für die Theorieprüfung in der Fahrschule. Diese Zusammenfassung behandelt Geschwindigkeitsbegrenzungen, Sicherheitsabstände, Verkehrszeichen und wichtige Berechnungen für Reaktions- und Bremswege. Ideal für angehende Fahrer, die sich optimal vorbereiten möchten.

1179.5892.239
Deutsch

Charaktere aus Heimsuchung von Jenny Erpenbeck

Mindmap, Allgemeines, Verlauf

1221.974358
Lerntipps

Führerschein Theorie Wiederholung/Notizen

Schilder, Zeichen, Zahlen, Vorfahrt und mehr - alles für die theoretische Führerscheinprüfung :)

1010.941190
Deutsch

Kapitelzusammenfassung Heimsuchung Jenny Erpenbeck

Zusammenfassung jeder Kapitel, Deutungen und Erklärungen

1217.027207
Deutsch

Heimsuchung - Erpenbeck Kapitelzusammenfassung

Kapitelübersichten von Heimsuchung (Jenny Erpenbeck) mit Seitenanzahl, Kapitelname und Inhaltszusammenfassung

123.63363

Schüler lieben uns, und du auch.

4.6/5App Store
4.7/5Google Play
Stefan SiOS-Nutzer

Die App ist sehr einfach zu bedienen und gut gestaltet. Ich habe bisher alles gefunden, wonach ich gesucht habe, und konnte viel aus den Präsentationen lernen! Ich werde die App definitiv für ein Schulprojekt nutzen! Und natürlich hilft sie auch sehr als Inspiration.

Samantha KlichAndroid-Nutzerin

Diese App ist wirklich super. Es gibt so viele Lernzettel und Hilfen [...]. Mein Problemfach ist zum Beispiel Französisch und die App hat so viele Möglichkeiten zur Hilfe. Dank dieser App habe ich mich in Französisch verbessert. Ich würde sie jedem empfehlen.

AnnaiOS-Nutzerin

Wow, ich bin wirklich begeistert. Ich habe die App einfach mal ausprobiert, weil ich sie schon oft beworben gesehen habe und war absolut beeindruckt. Diese App ist DIE HILFE, die man für die Schule braucht und vor allem bietet sie so viele Dinge wie Übungen und Lernzettel, die mir persönlich SEHR geholfen haben.