Halbwertszeit und Verdopplungszeit verstehen

Du kennst das bestimmt: Bei exponentiellen Prozessen ändert sich etwas konstant - entweder wächst es oder schrumpft es. Die Verdopplungszeit zeigt dir, wann sich ein Wert verdoppelt hat, während die Halbwertszeit angibt, wann nur noch die Hälfte übrig ist.

Bevor du losrechnest, brauchst du den Wachstumsfaktor. Den findest du mit der Formel b = 1 + p/100, wobei p der Prozentsatz ist.

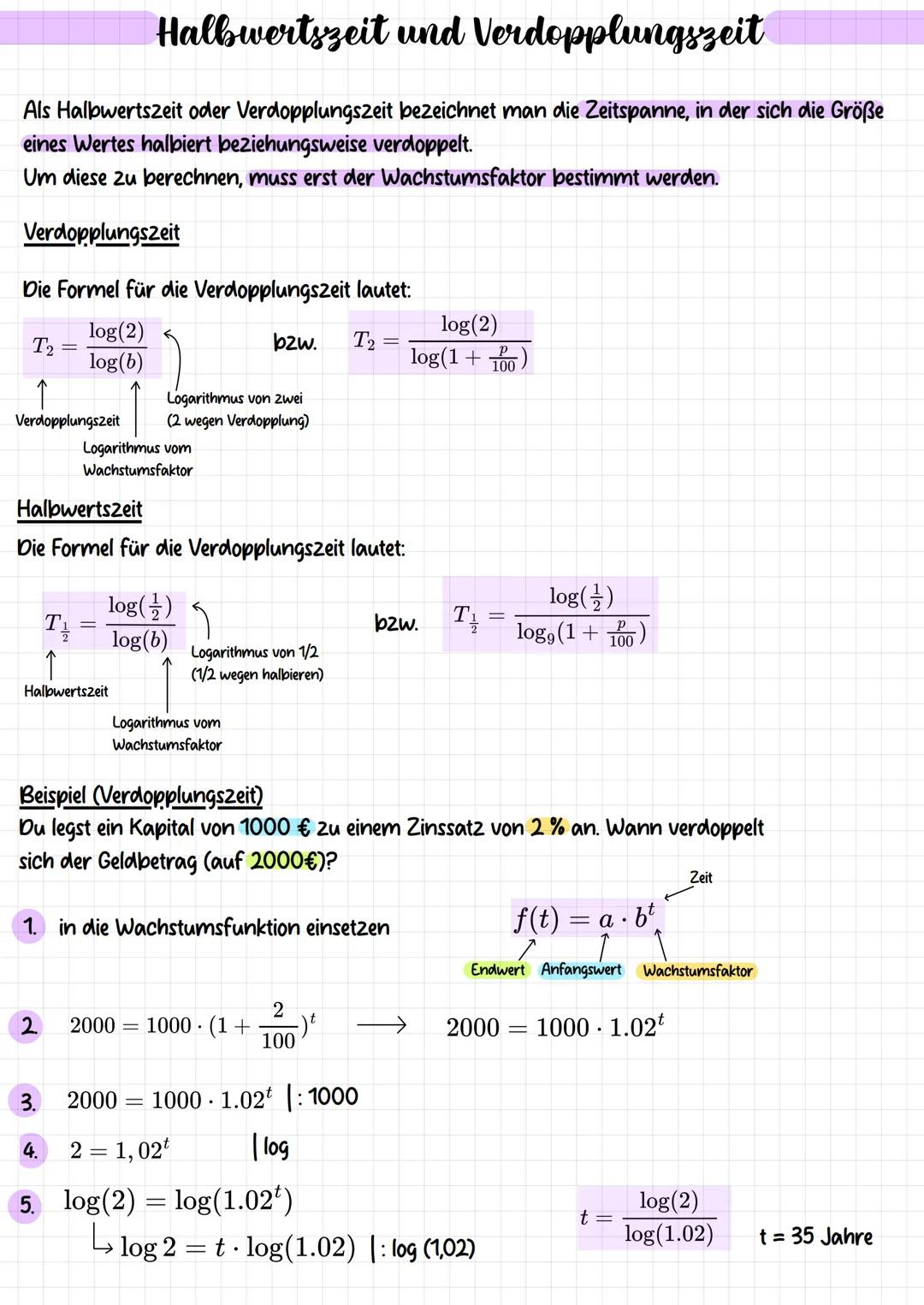
Verdopplungszeit berechnen: $T_2 = \frac{log(2)}{log(b)}$ Die 2 steht für die Verdopplung, b ist dein Wachstumsfaktor.

Halbwertszeit berechnen: $T_{\frac{1}{2}} = \frac{log(\frac{1}{2})}{log(b)}$ Hier steht 1/2 für die Halbierung.

Merktipp: Der Zähler zeigt immer an, was passiert $verdoppeln = 2, halbieren = 1/2$. Der Nenner ist immer der Logarithmus deines Wachstumsfaktors!

Das Praxisbeispiel macht's klar: 1000€ bei 2% Zinsen werden zu 2000€. Mit der Formel $t = \frac{log(2)}{log(1,02)}$ kommst du auf 35 Jahre. So einfach ist das!