Analytische Geometrie - Koordinatensysteme und Vierecke
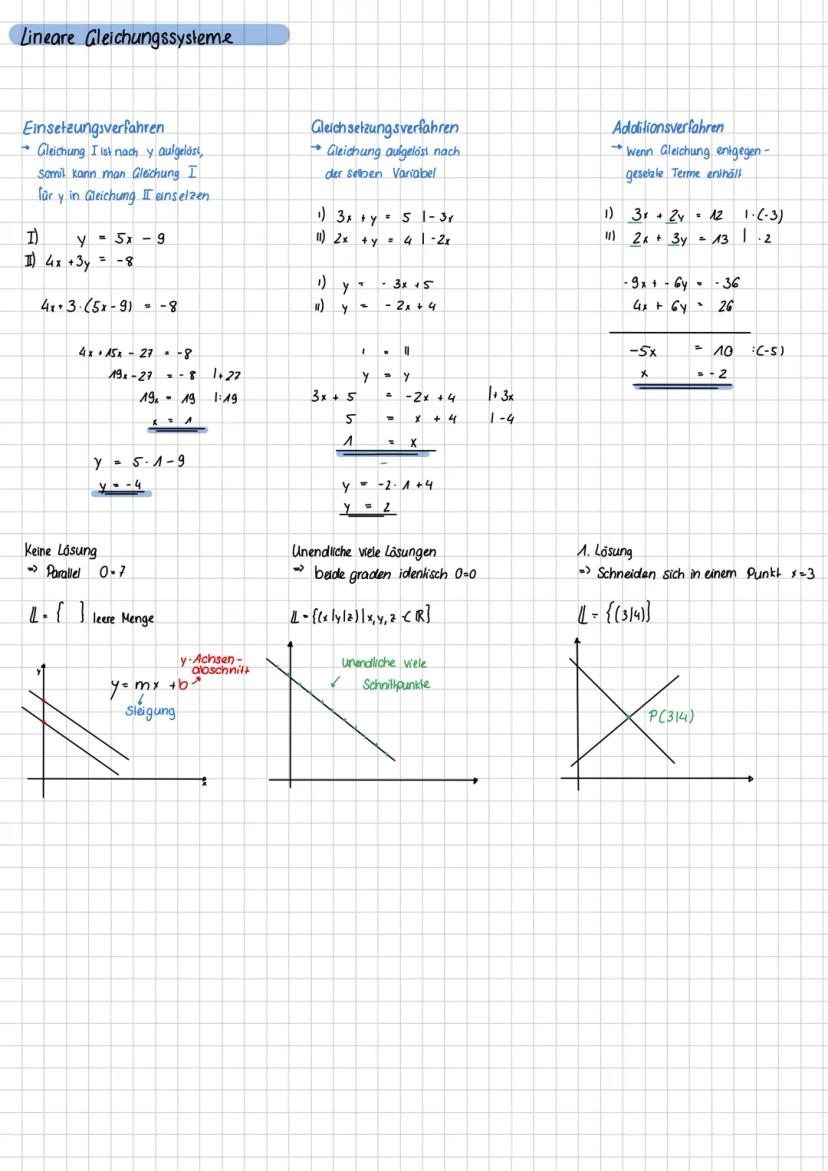
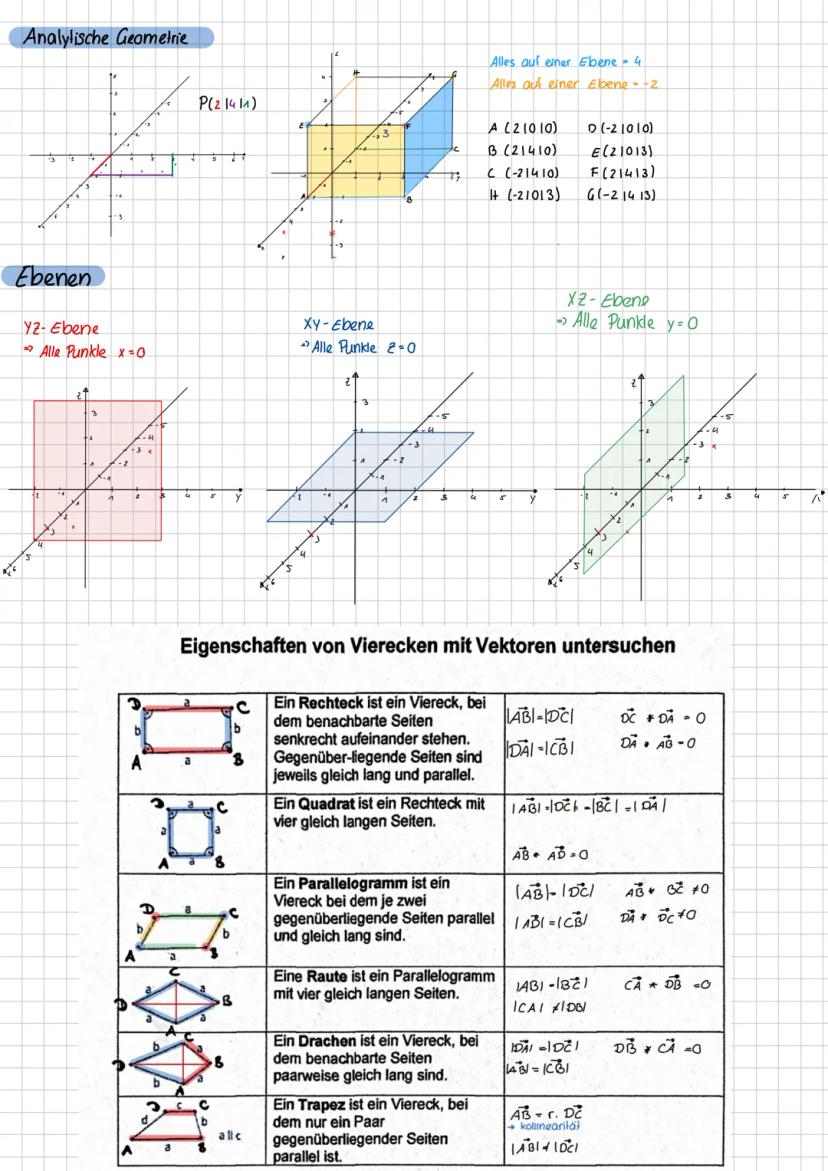
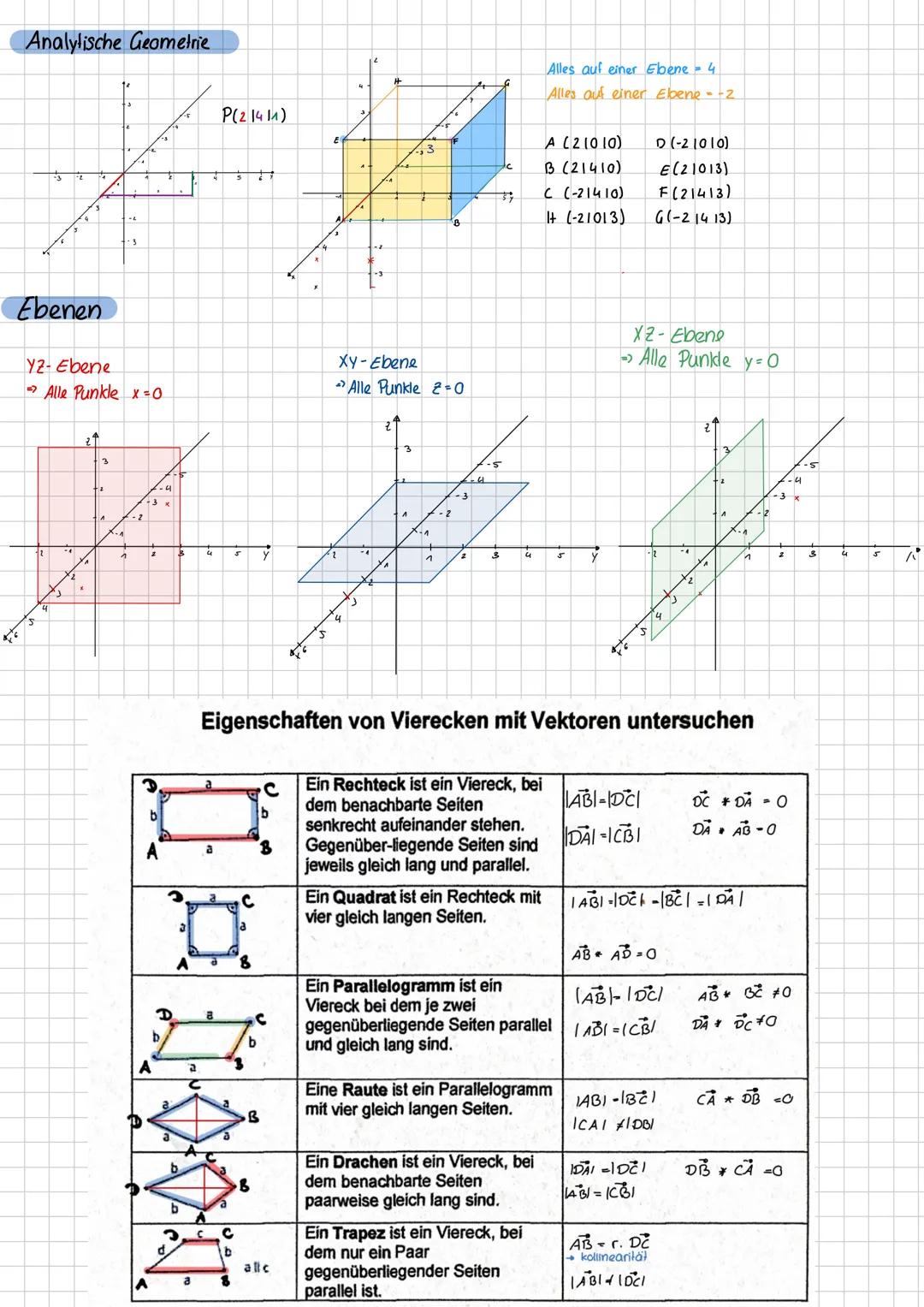
In der analytischen Geometrie beschreibst du geometrische Objekte mit Koordinaten und Vektoren. Die drei Koordinatenebenen xy−,xz−,yz−Ebene entstehen, wenn eine der drei Koordinaten null ist.
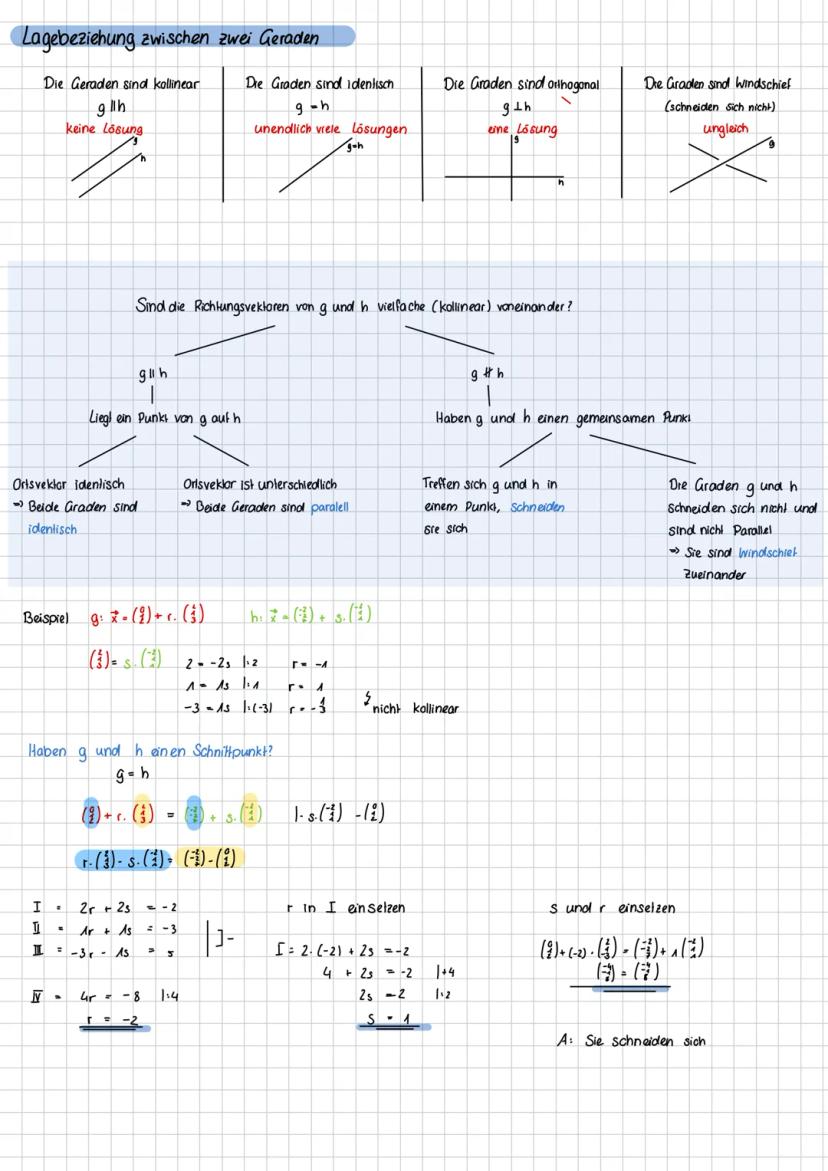
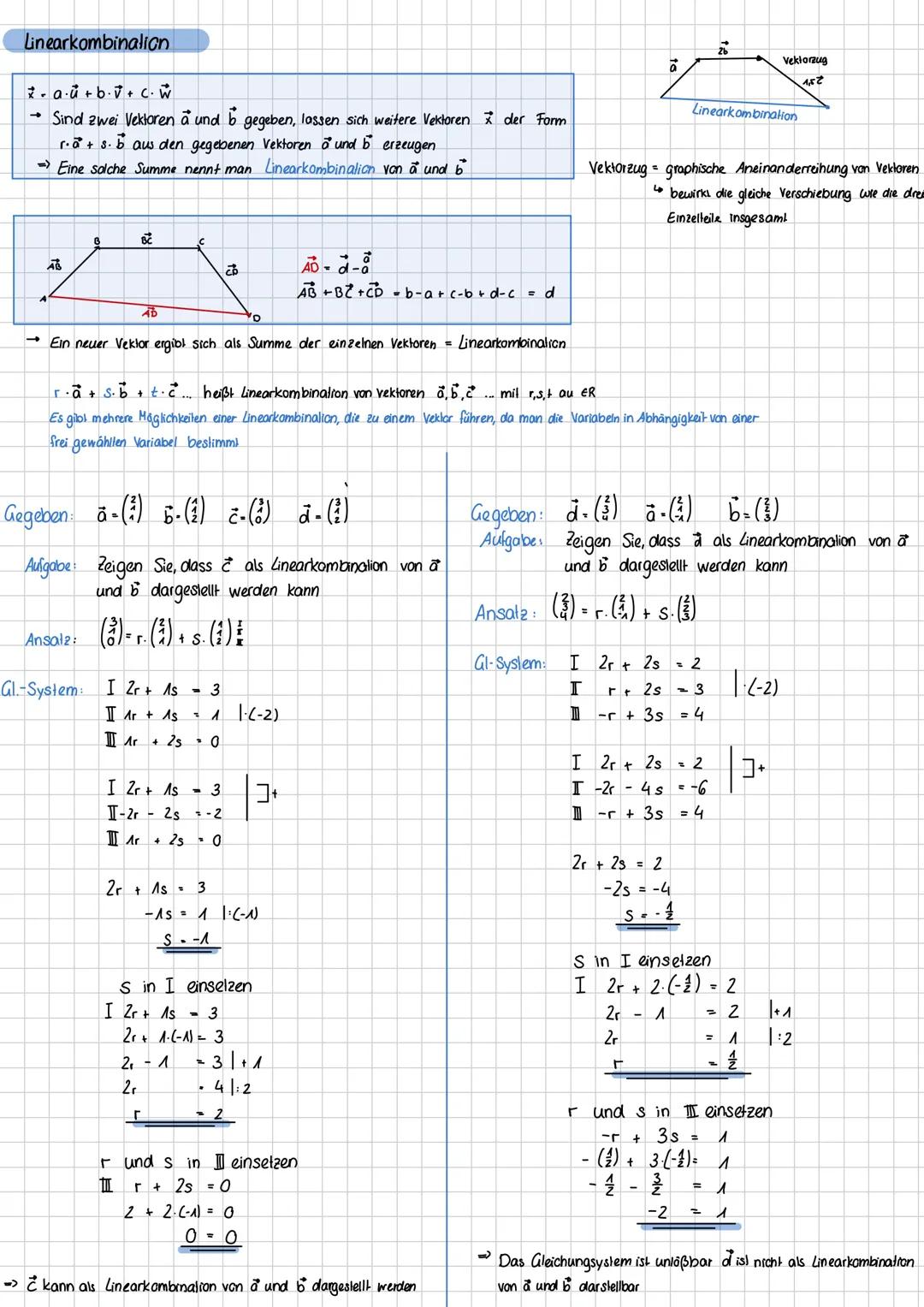
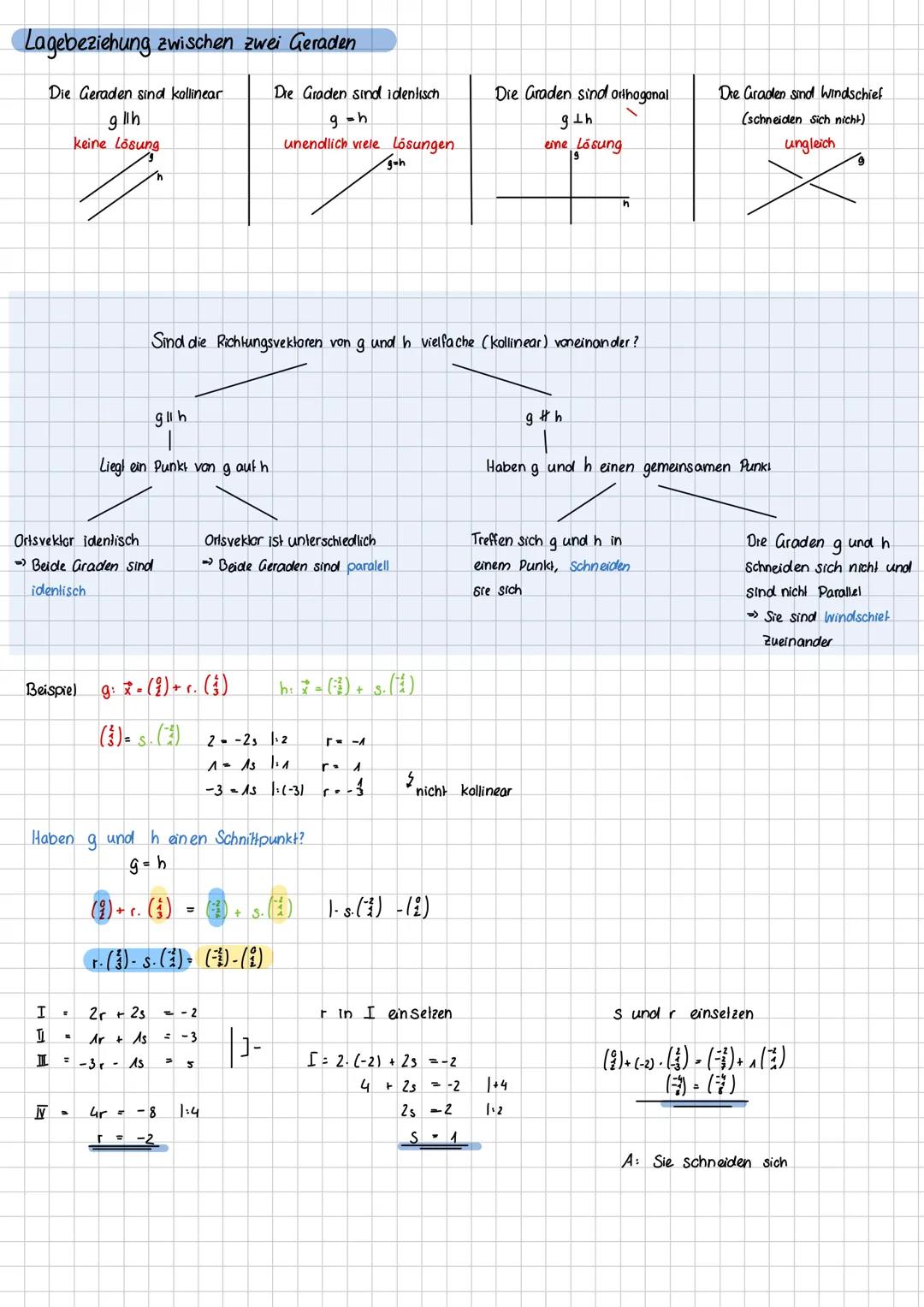
Vierecke lassen sich perfekt mit Vektoren untersuchen. Ein Rechteck hat senkrechte benachbarte Seiten Skalarprodukt=0 und gleich lange Gegenseiten. Bei einem Quadrat sind zusätzlich alle Seiten gleich lang.
Parallelogramme haben parallele und gleich lange Gegenseiten, Rauten sind Parallelogramme mit vier gleich langen Seiten. Trapeze haben nur ein Paar paralleler Seiten, während Drachen paarweise gleich lange benachbarte Seiten besitzen.
Praxistipp: Zeichne dir die Vierecke auf und markiere die charakteristischen Eigenschaften - das hilft beim Lösen von Aufgaben enorm!