Mathe-Themen Überblick

Du stehst vor zwei mega wichtigen Mathe-Kapiteln! Lineare Funktionen zeigen dir, wie Geraden im Koordinatensystem funktionieren. Lineare Gleichungssysteme helfen dir dabei, Aufgaben mit mehreren Unbekannten zu knacken.

Diese beiden Themen hängen eng zusammen - wenn du Funktionen verstehst, werden dir Gleichungssysteme viel leichter fallen. Du wirst sehen, dass alles logisch aufeinander aufbaut!

Lineare Funktionen - Die Basics

Stell dir vor, du zeichnest eine gerade Linie im Koordinatensystem - das ist eine lineare Funktion! Die Formel f(x) = mx + b ist dein wichtigster Begleiter. Das "x" steht immer ohne Potenz da (nie x² oder x³), deshalb heißt es auch Funktion ersten Grades.

m ist die Steigung - sie zeigt dir, ob die Gerade steigt (m > 0), waagerecht verläuft $m = 0$ oder fällt (m < 0). b ist der y-Achsenabschnitt - der Punkt, wo deine Gerade die y-Achse schneidet.

Mit dem Steigungsdreieck findest du die Steigung raus: Du zählst einfach die Länge der senkrechten Seite und teilst sie durch die waagerechte Seite. Das ergibt einen Bruch, der deine Steigung ist!

Merktipp: Bei linearen Funktionen mit b = 0 spricht man von Ursprungsgeraden - sie gehen direkt durch den Nullpunkt!

Steigung berechnen und wichtige Punkte finden

Die Steigungsformel m = $y₂-y₁$/$x₂-x₁$ ist dein Geheimrezept! Du suchst dir zwei markante Punkte auf der Geraden aus und setzt ihre Koordinaten in die Formel ein. Super praktisch, wenn das Steigungsdreieck schwer abzulesen ist.

Den Y-Achsenabschnitt findest du, indem du schaust, wo die Gerade die y-Achse schneidet. Bei der Funktion f(x) = 2x - 3 ist der y-Achsenabschnitt einfach -3.

Nullstellen berechnen funktioniert anders: Du setzt f(x) = 0 und löst nach x auf. Bei 0 = -2x + 1 rechnest du +2x, dann durch 2 teilen und kriegst x = 1/2. Die Nullstelle liegt also bei (1/2|0).

Praxis-Tipp: Nullstellen sind mega wichtig für Textaufgaben - sie zeigen dir oft, wann etwas den Wert Null erreicht!

Funktionsgraphen zeichnen und Gleichungen bestimmen

Funktionsgraph zeichnen ist wie ein Rezept: Erst den y-Achsenabschnitt einzeichnen, dann die Steigung ablesen und das Steigungsdreieck vom y-Achsenabschnitt aus zeichnen. Bei f(x) = 2/4 x + 2 gehst du 4 Schritte nach rechts und 2 nach oben. Zum Schluss verbindest du die Punkte mit einer geraden Linie.

Funktionsgleichung bestimmen geht zwei Wege: Wenn der Graph da ist, liest du b ab und zeichnest ein Steigungsdreieck für m. Wenn du nur zwei Punkte hast, berechnest du erst m mit der Steigungsformel, dann setzt du einen Punkt in y = mx + b ein und löst nach b auf.

Beispiel: P(5|6) und Q(4|3) ergeben m = (3-6)/(4-5) = 3. Mit P eingesetzt: 6 = 3·5 + b, also b = -9. Fertig: f(x) = 3x - 9!

Erfolgs-Tipp: Mach immer eine Probe mit dem zweiten Punkt - so merkst du Rechenfehler sofort!

Besondere Geraden und ihre Lage

Waagerechte Geraden haben die Steigung m = 0 und die Gleichung f(x) = b. Sie verlaufen parallel zur x-Achse - total einfach zu zeichnen! Senkrechte Geraden sind technisch keine Funktionen mehr, weil einem x-Wert unendlich viele y-Werte zugeordnet sind. Ihre Gleichung ist einfach x = c.

Parallele Geraden haben dieselbe Steigung, aber verschiedene y-Achsenabschnitte. Sie treffen sich nie! Geraden mit eindeutigem Schnittpunkt haben verschiedene Steigungen.

Den Schnittpunkt findest du, indem du die Funktionen gleichsetzt: f(x) = g(x). Das ergibt eine Gleichung mit nur noch x, die du lösen kannst. Den x-Wert setzt du dann in eine der Funktionen ein, um den y-Wert zu bekommen.

Wichtig: Mach immer die Probe, indem du x auch in die andere Funktion einsetzt!

Schnittpunkte berechnen - Schritt für Schritt

Bei Schnittpunkten checkst du erst: Haben die Geraden verschiedene Steigungen? Dann gibt's einen Schnittpunkt! Du setzt f(x) = g(x) und löst nach x auf.

Beispiel: f(x) = 2x - 2 und g(x) = -2/3x + 6. Gleichsetzen: 2x - 2 = -2/3x + 6. Nach x auflösen ergibt x = 3. Einsetzen in f(x): f(3) = 2·3 - 2 = 4. Probe: g(3) = -2/3·3 + 6 = 4 ✓

Grafisch geht's auch: Beide Funktionen zeichnen und den Schnittpunkt ablesen. Das ist super zur Kontrolle, aber rechnerisch ist meist genauer.

Der Schnittpunkt liegt also bei (3|4) - dort treffen sich beide Geraden!

Merktipp: Schnittpunkte von Geraden sind oft gefragt bei Textaufgaben - sie zeigen dir, wann zwei Situationen gleich sind!

Gleichungssysteme - Das Gleichsetzungsverfahren

Lineare Gleichungssysteme haben zwei Gleichungen mit zwei Unbekannten (x und y). Du suchst Zahlen, die beide Gleichungen gleichzeitig erfüllen - wie ein Rätsel mit zwei Hinweisen!

Beim Gleichsetzungsverfahren formst du beide Gleichungen nach derselben Variable um. Dann setzt du sie gleich und löst nach der anderen Variable auf.

Beispiel: Aus 2x - 3y = -2 wird x = -1 + 1,5y und aus -3x + 6y = 0 wird x = 2y. Gleichsetzen: -1 + 1,5y = 2y ergibt y = -2. Das setzt du in eine Gleichung ein: x = 2(-2) = -4.

Probe nicht vergessen! Setze x = -4 und y = -2 in beide ursprünglichen Gleichungen ein und check, ob's stimmt.

Erfolgs-Strategie: Das Gleichsetzungsverfahren ist perfekt, wenn eine Gleichung schon nach x oder y aufgelöst ist!

Besondere Fälle bei Gleichungssystemen

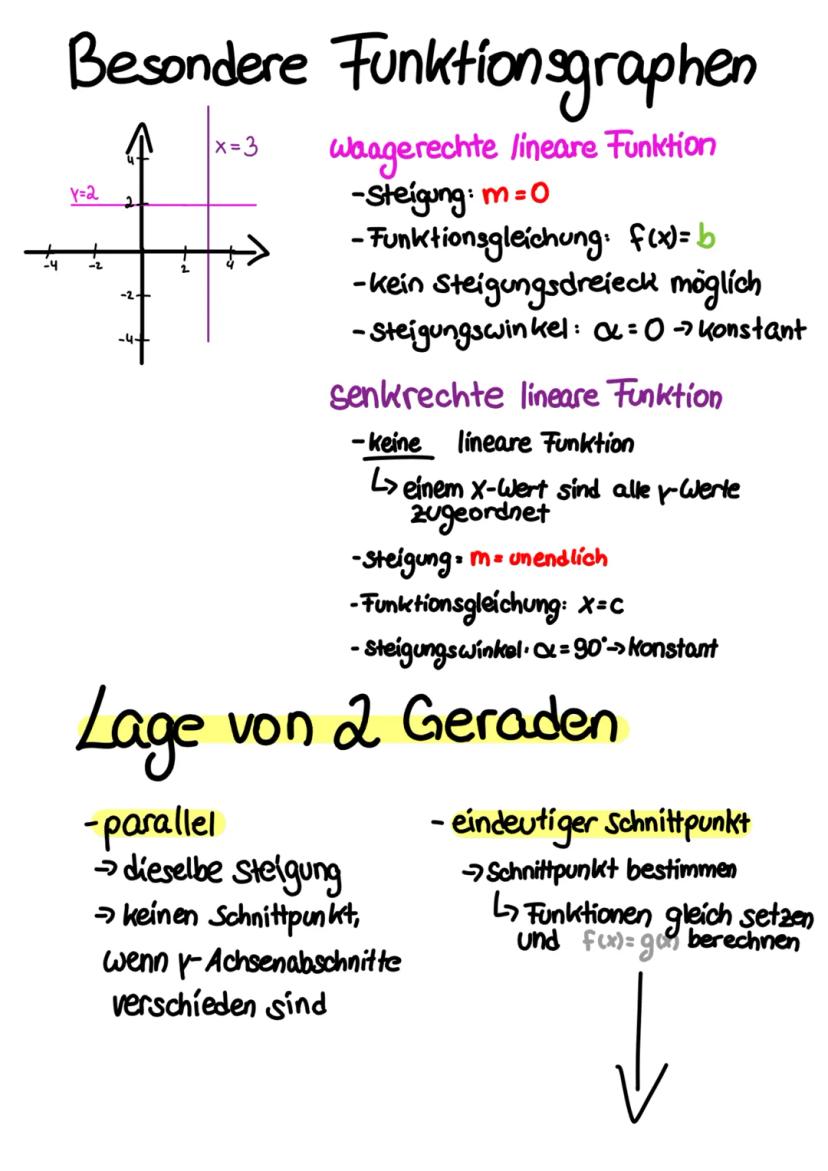
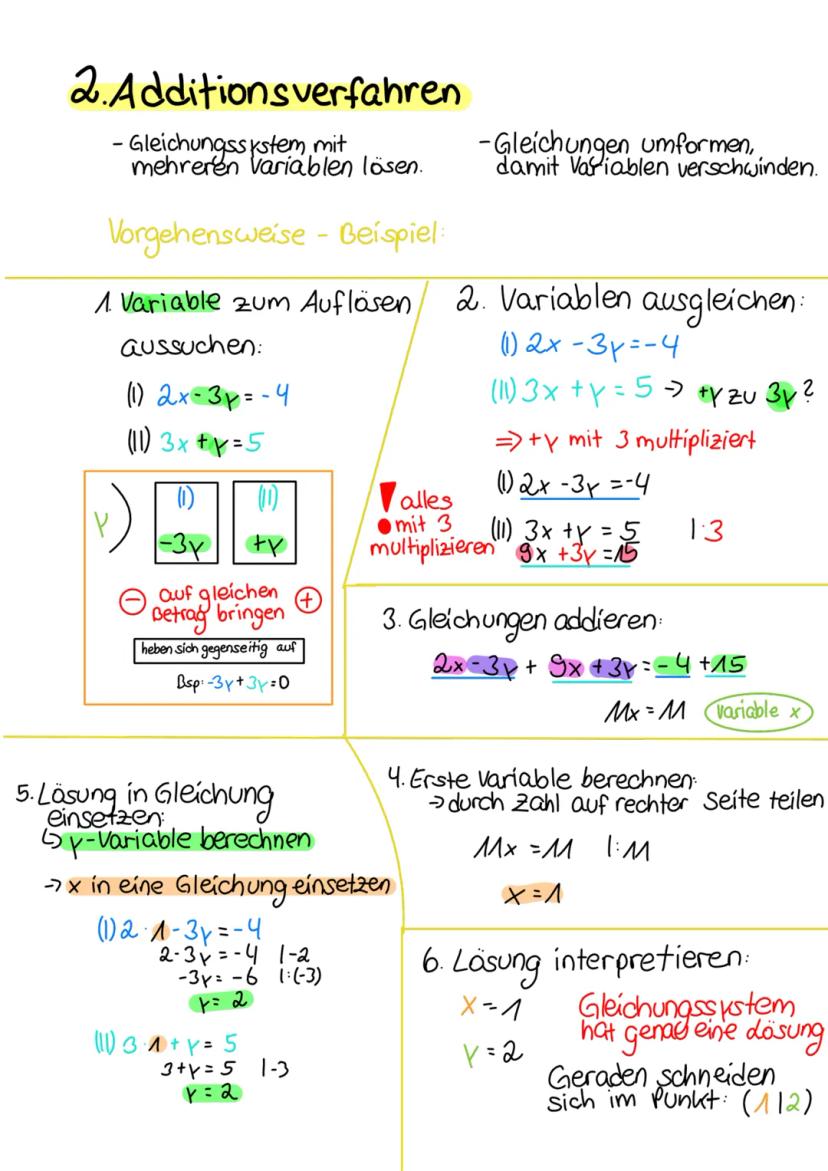
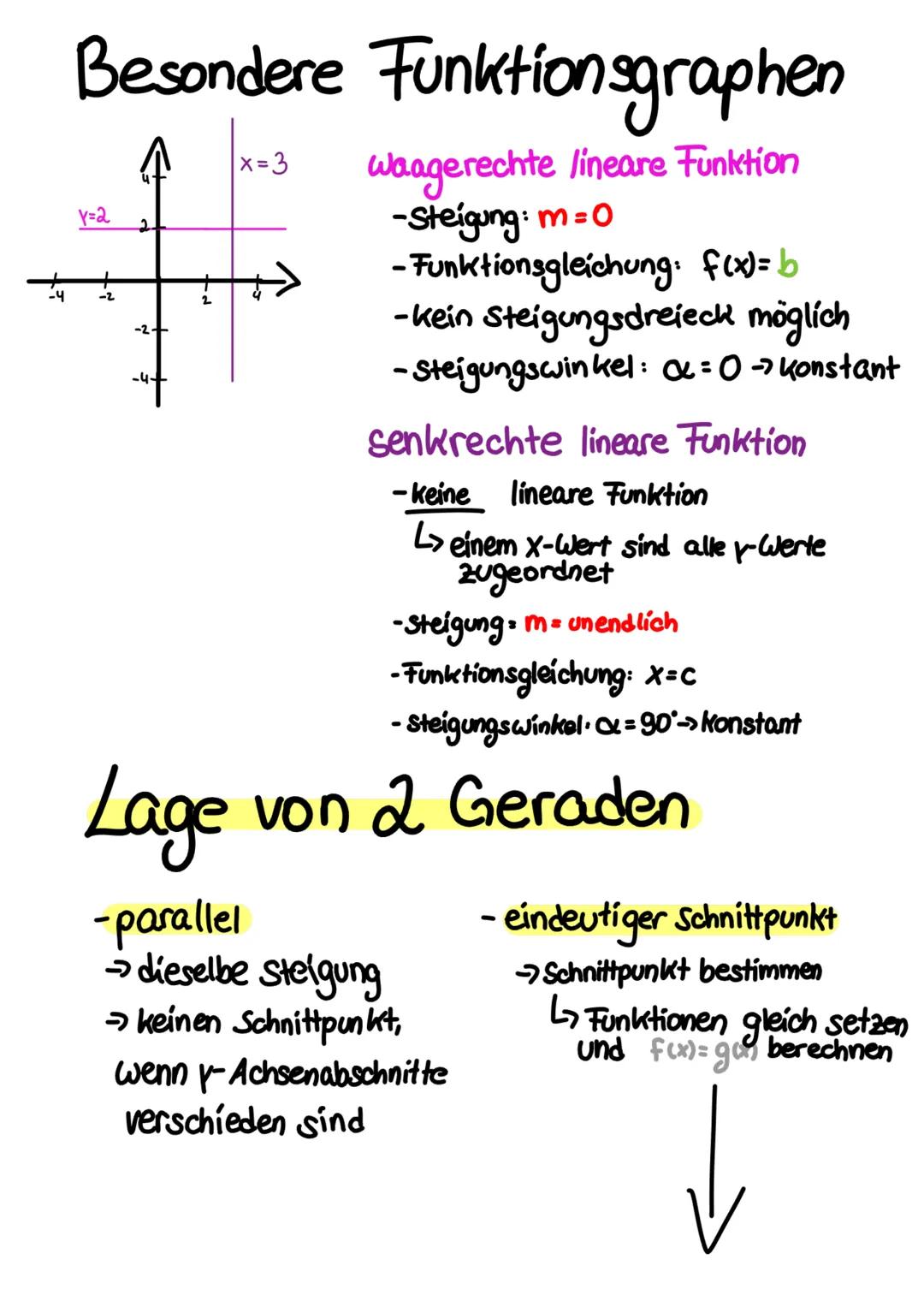
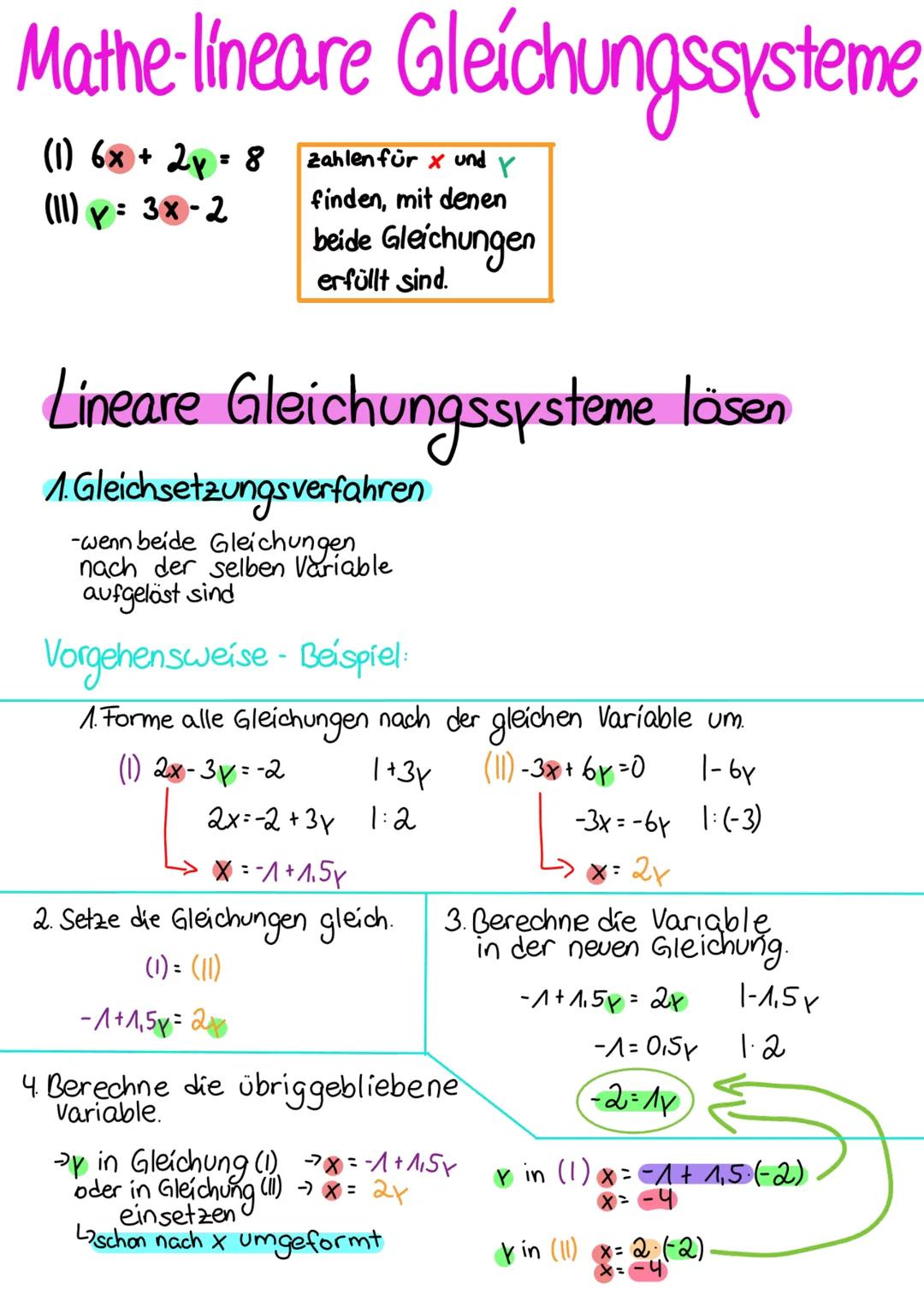
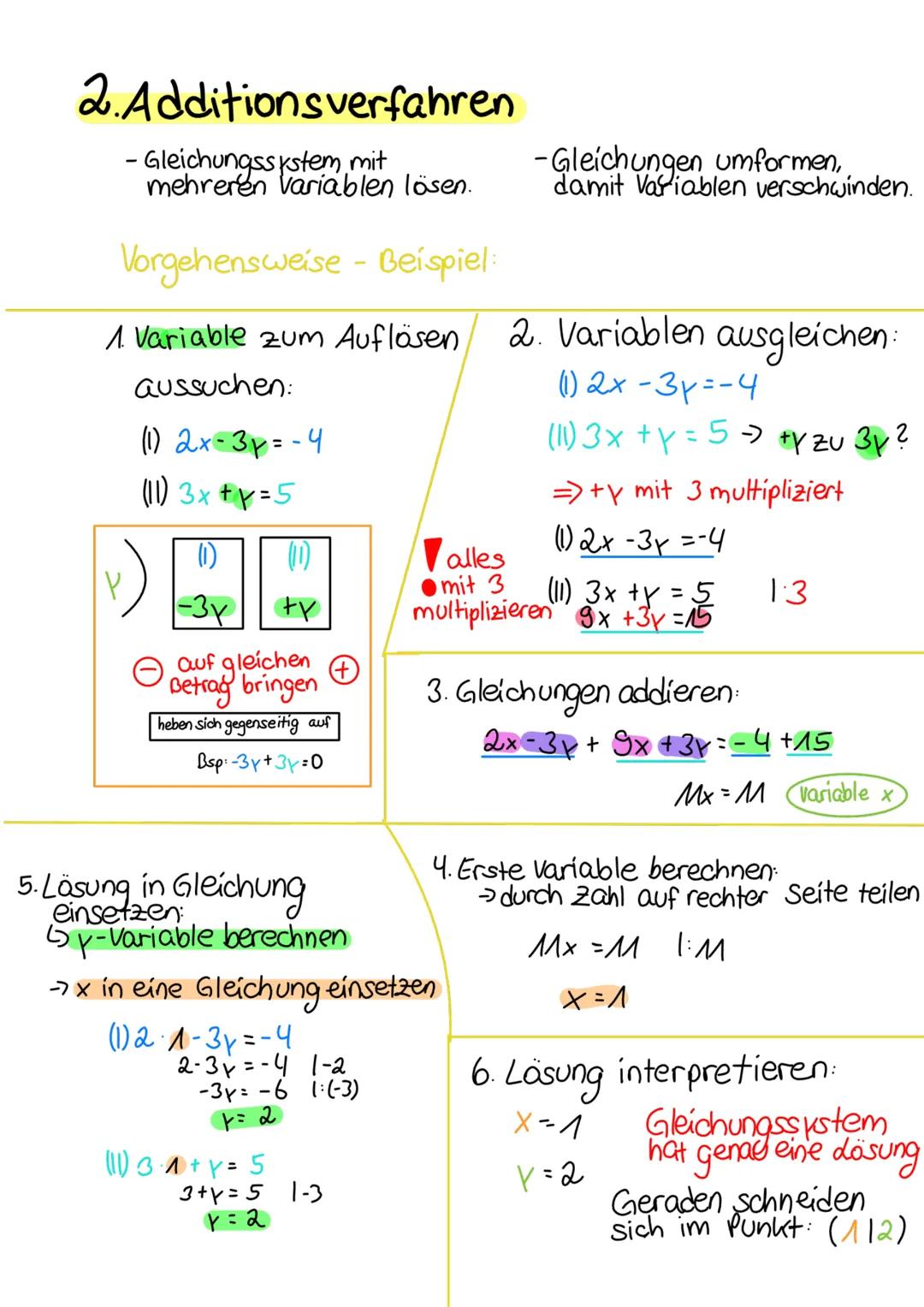
Manchmal läuft's anders als geplant! Wenn du beim Gleichsetzen so etwas wie -1 = 1,5 rausbekommst (eine falsche Aussage), dann hat das Gleichungssystem keine Lösung. Die Geraden verlaufen parallel zueinander.

Kriegst du dagegen 0 = 0 oder 3,5 = 3,5 raus (eine immer wahre Aussage), dann hat das System unendlich viele Lösungen. Die beiden Gleichungen beschreiben eigentlich dieselbe Gerade!

Beispiel für keine Lösung: -3x + 6y = 3 und 2x - 4y = 3 ergeben nach Umformen -1 = 1,5. Unmöglich!

Beispiel für unendlich viele Lösungen: 2x - 5y = 7 und -4x + 10y = -14 ergeben beide x = 3,5 + 2,5y. Identisch!

Wichtig: Diese besonderen Fälle kommen in Tests gerne vor - lass dich nicht verwirren!

Das Additionsverfahren meistern

Das Additionsverfahren ist mega clever: Du formst die Gleichungen so um, dass sich eine Variable beim Addieren weghebt! Dann hast du nur noch eine Variable übrig.

Schritt-für-Schritt: Bei 2x - 3y = -4 und 3x + y = 5 multiplizierst du die zweite Gleichung mit 3, damit aus +y wird +3y. Jetzt hast du -3y und +3y, die sich zu 0 addieren.

Nach dem Multiplizieren: 2x - 3y = -4 und 9x + 3y = 15. Addieren: 11x = 11, also x = 1. Das x setzt du in eine ursprüngliche Gleichung ein: 3(1) + y = 5, also y = 2.

Lösung: x = 1, y = 2. Das bedeutet: Die Geraden schneiden sich im Punkt (1|2)!

Pro-Tipp: Das Additionsverfahren ist super, wenn die Koeffizienten schon ähnlich sind oder leicht angepasst werden können!

Besondere Fälle beim Additionsverfahren

Auch beim Additionsverfahren gibt's diese besonderen Situationen! Wenn du die Gleichungen addierst und 0 = 21 (oder eine andere falsche Zahl) rauskommt, hat das System keine Lösung. Die Geraden sind parallel.

Kommt 0 = 0 raus, hat das System unendlich viele Lösungen. Die Gleichungen beschreiben dieselbe Gerade - sie "berühren" sich an allen Punkten.

Beispiel keine Lösung: -3x + 6y = 6 und 3x - 6y = 15 ergeben beim Addieren 0 = 21. Unmöglich!

Beispiel unendlich viele Lösungen: 8x - 2y = 6 und -8x + 2y = -6 ergeben 0 = 0. Die Gleichungen sind identisch!

Durchblick-Tipp: Egal welches Verfahren du verwendest - die besonderen Fälle erkennst du immer an falschen Aussagen (keine Lösung) oder wahren Aussagen wie 0 = 0 (unendlich viele Lösungen)!