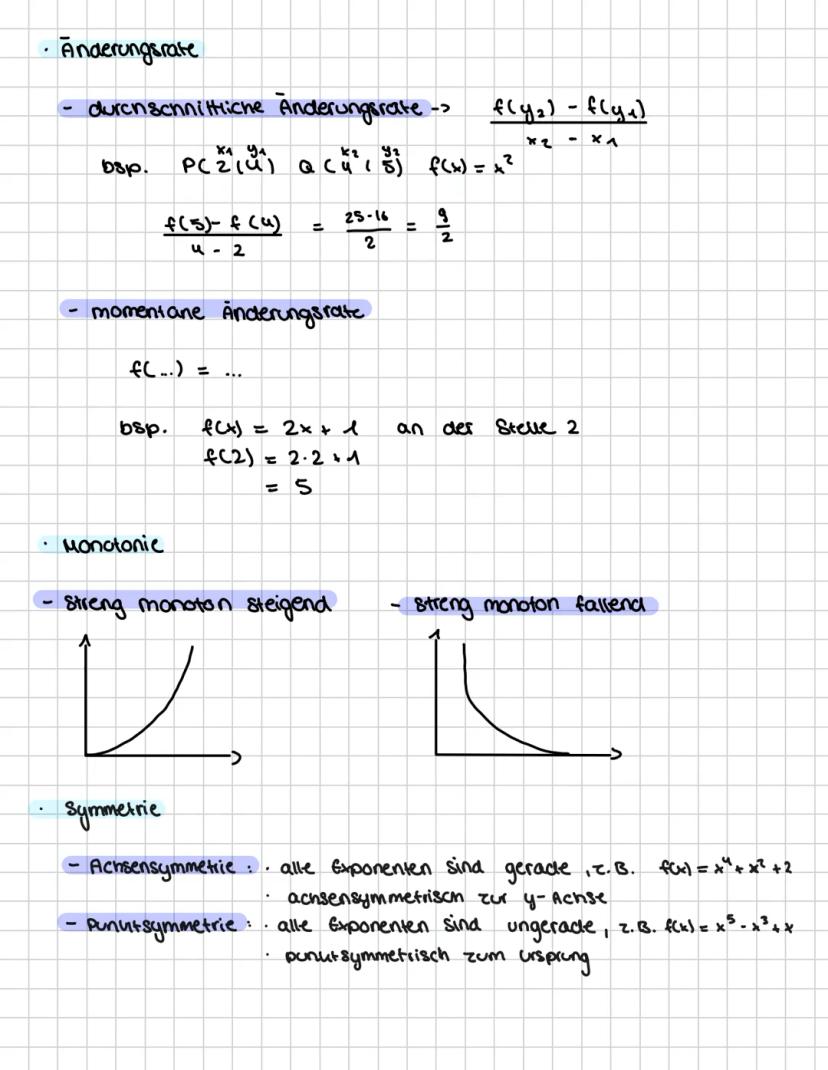
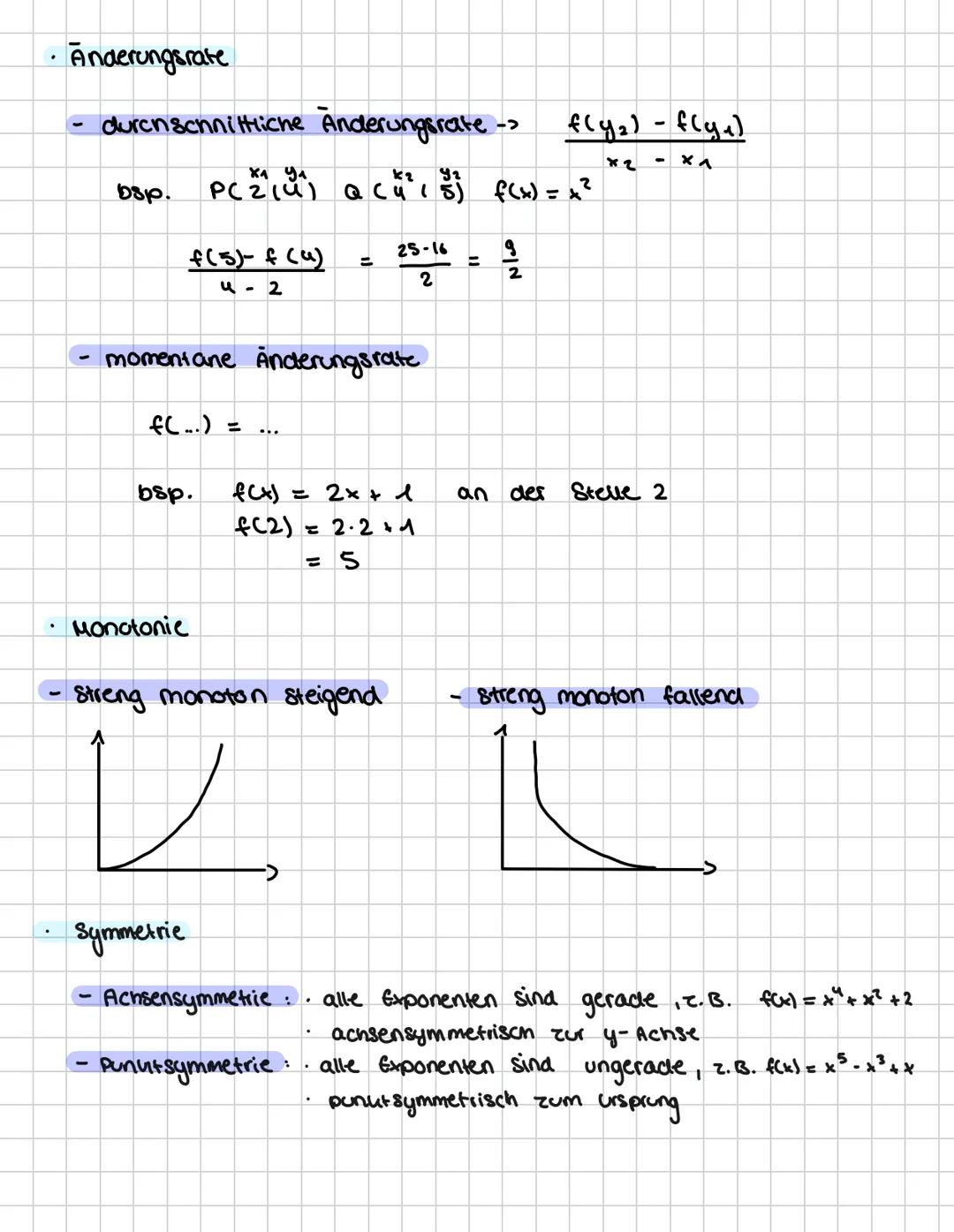
Mathe Leistungskurs kann erstmal überwältigend wirken, aber keine Sorge! Diese... Mehr anzeigen
Melde dich an, um den Inhalt zu sehenKostenlos!
Zugriff auf alle Dokumente
Verbessere deine Noten
Schließ dich Millionen Schülern an
Mit der Anmeldung akzeptierst du die Nutzungsbedingungen und Datenschutzerklärung