Die Ableitungsfunktion – grafisches Ableiten

Stell dir vor, du fährst mit dem Auto eine kurvige Straße entlang – die Ableitungsfunktion f'$x$ zeigt dir genau, wie steil es gerade bergauf oder bergab geht! Sie ordnet jedem x-Wert die Steigung des Funktionsgraphen an dieser Stelle zu.

Das grafische Ableiten funktioniert nach einem einfachen Prinzip: Wo das ursprüngliche Schaubild steigt (positive Steigung), verläuft f'$x$ oberhalb der x-Achse. Wo es fällt (negative Steigung), liegt f'$x$ unterhalb der x-Achse.

Besonders wichtig sind die Stellen, wo die Steigung null ist – dort schneidet f'$x$ die x-Achse. Das sind genau die Punkte, wo die ursprüngliche Funktion ihre Extremstellen hat!

Merktipp: Die Ableitung f'$x$ ist wie ein "Steigungsmesser" für jede Stelle der ursprünglichen Funktion.

Extremstellen, Maximum, Minimum

Extremstellen sind die "Berggipfel" und "Täler" einer Funktion – und die zu finden ist gar nicht schwer! Es gibt lokale Extrema (die höchsten/tiefsten Punkte in einer kleinen Umgebung) und globale Extrema (die absoluten Rekordhalter im gesamten Definitionsbereich).

Ein lokales Maximum liegt vor, wenn f(x₀) ≥ f$x$ in der Umgebung von x₀ gilt. Beim lokalen Minimum ist es umgekehrt: f(x₀) ≤ f$x$ in der Umgebung.

Aufpassen musst du bei Randextrema – die liegen am Rand des Definitionsbereichs und verhalten sich manchmal anders als "normale" Extremstellen. Im Beispiel siehst du: T₁(1|1,5) und T₂(4|1,5) sind Tiefpunkte, H₂(2|3) ist ein Hochpunkt.

Praxistipp: Schaue immer zuerst auf den Definitionsbereich – manche Extrema verstecken sich am Rand!

Extrempunkte und Ableitungen

Jetzt wird's richtig praktisch: Mit den Ableitungen kannst du Extrempunkte mathematisch beweisen! Es gibt zwei super Methoden, die du beide draufhaben solltest.

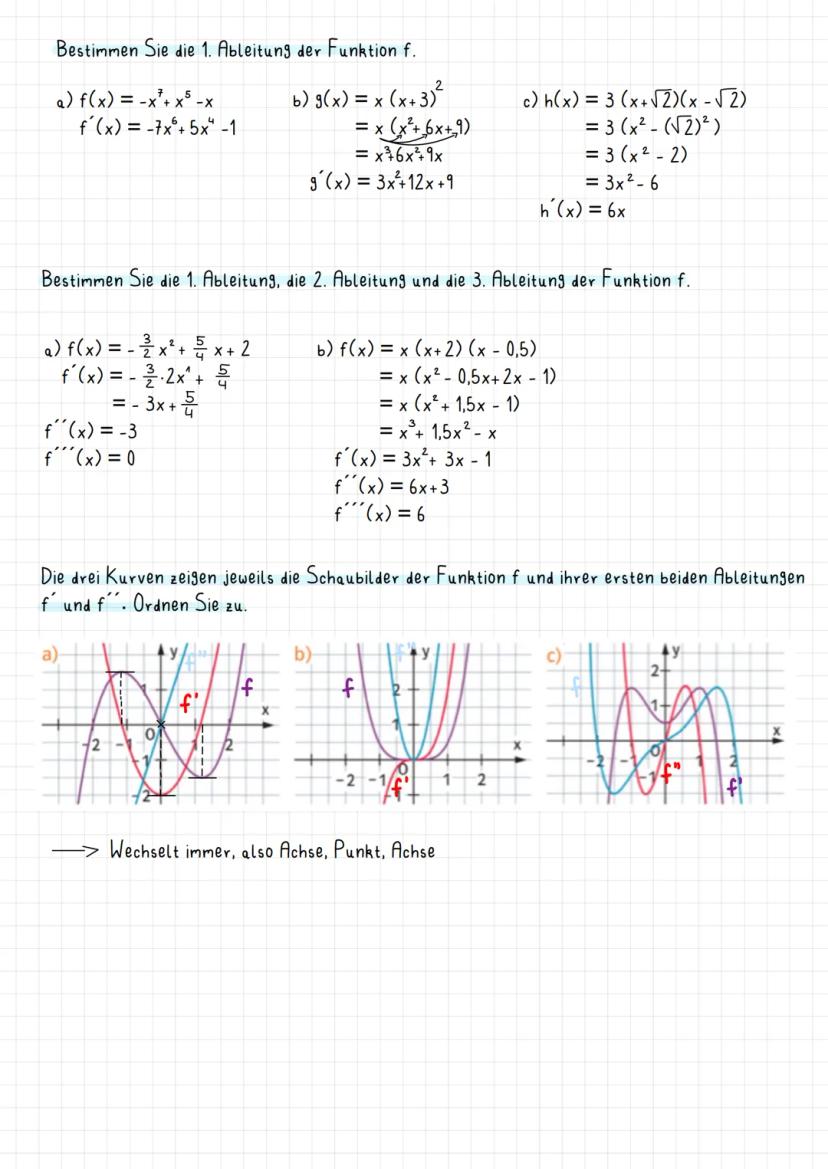
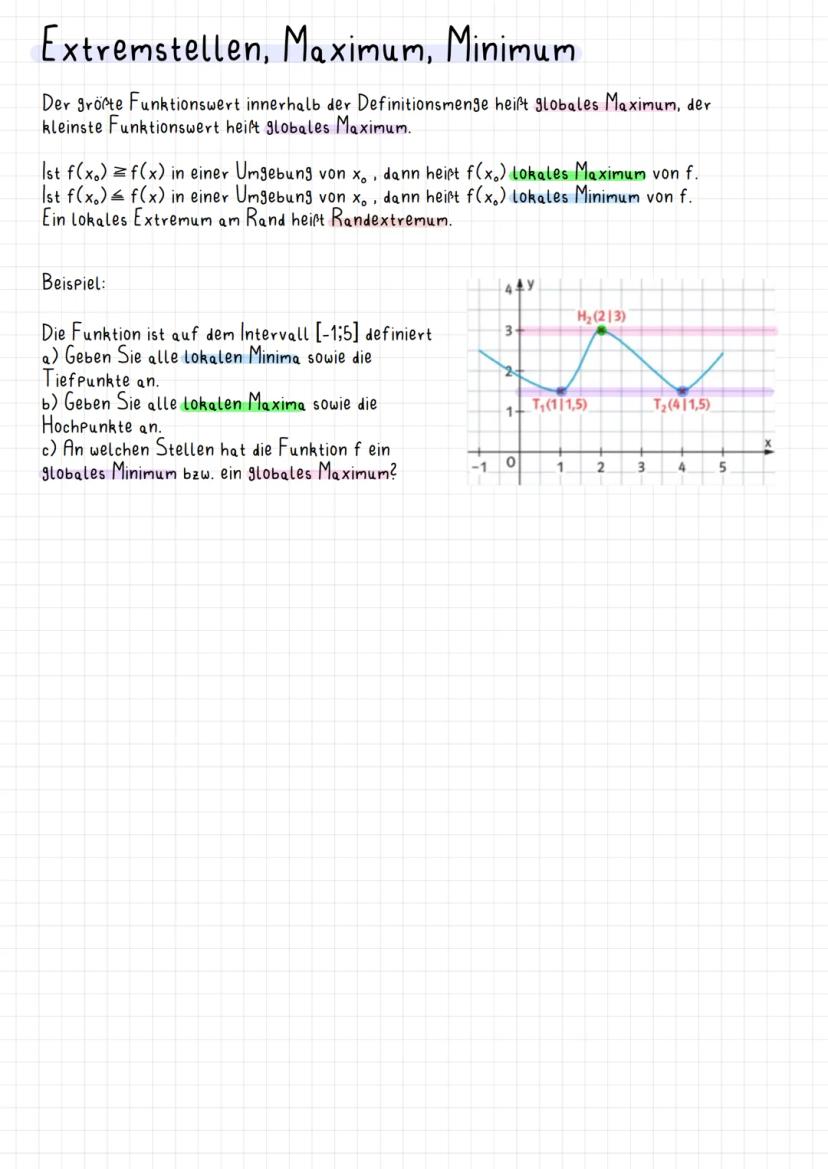
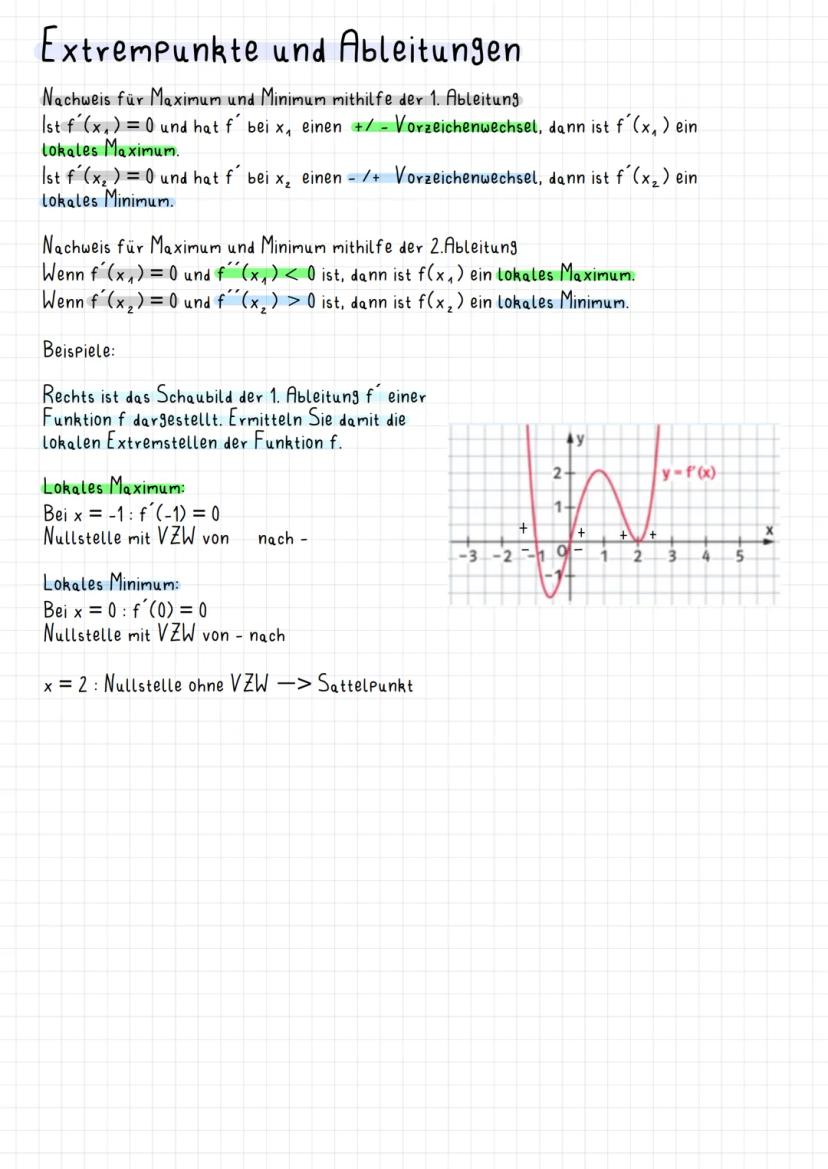
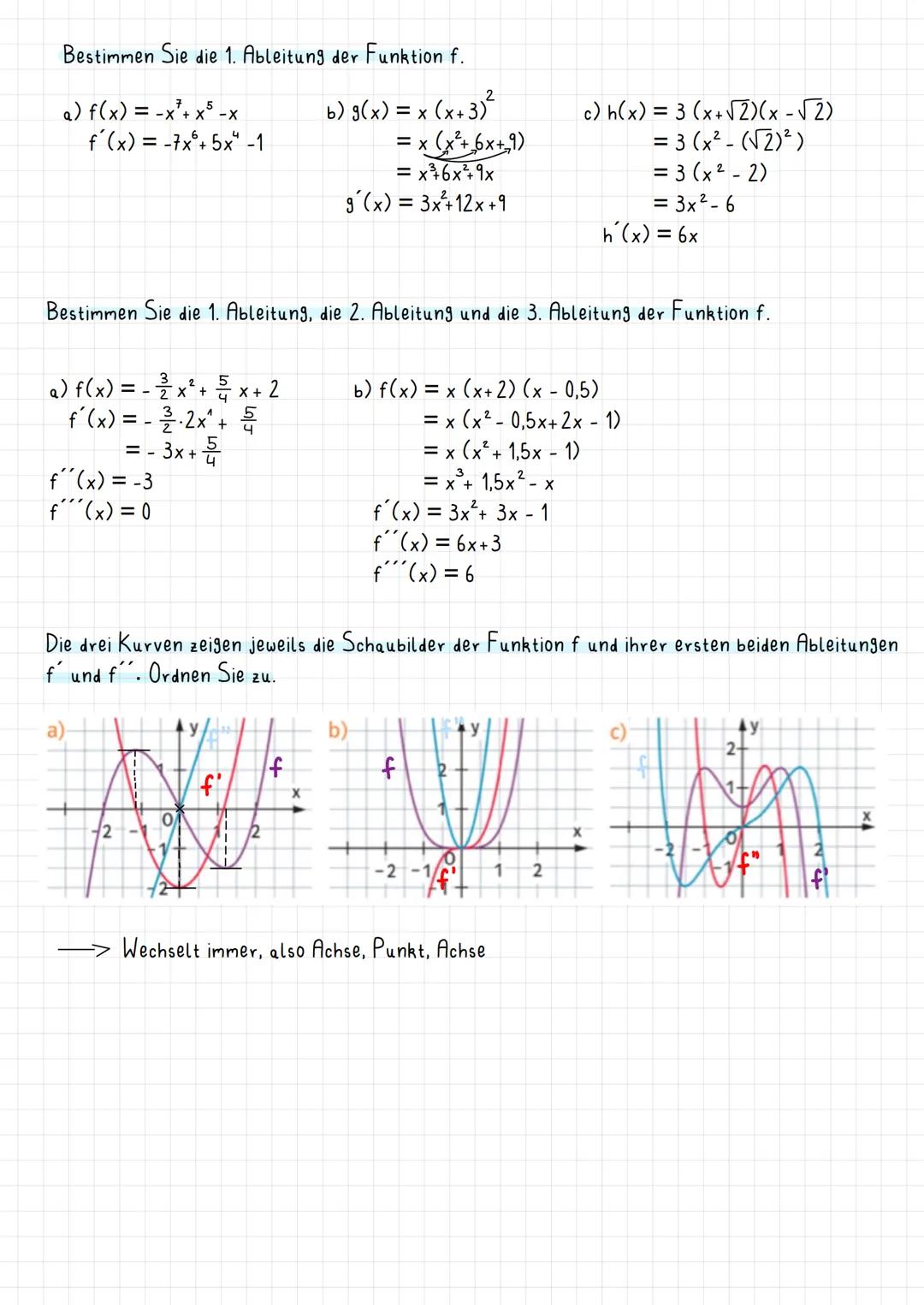
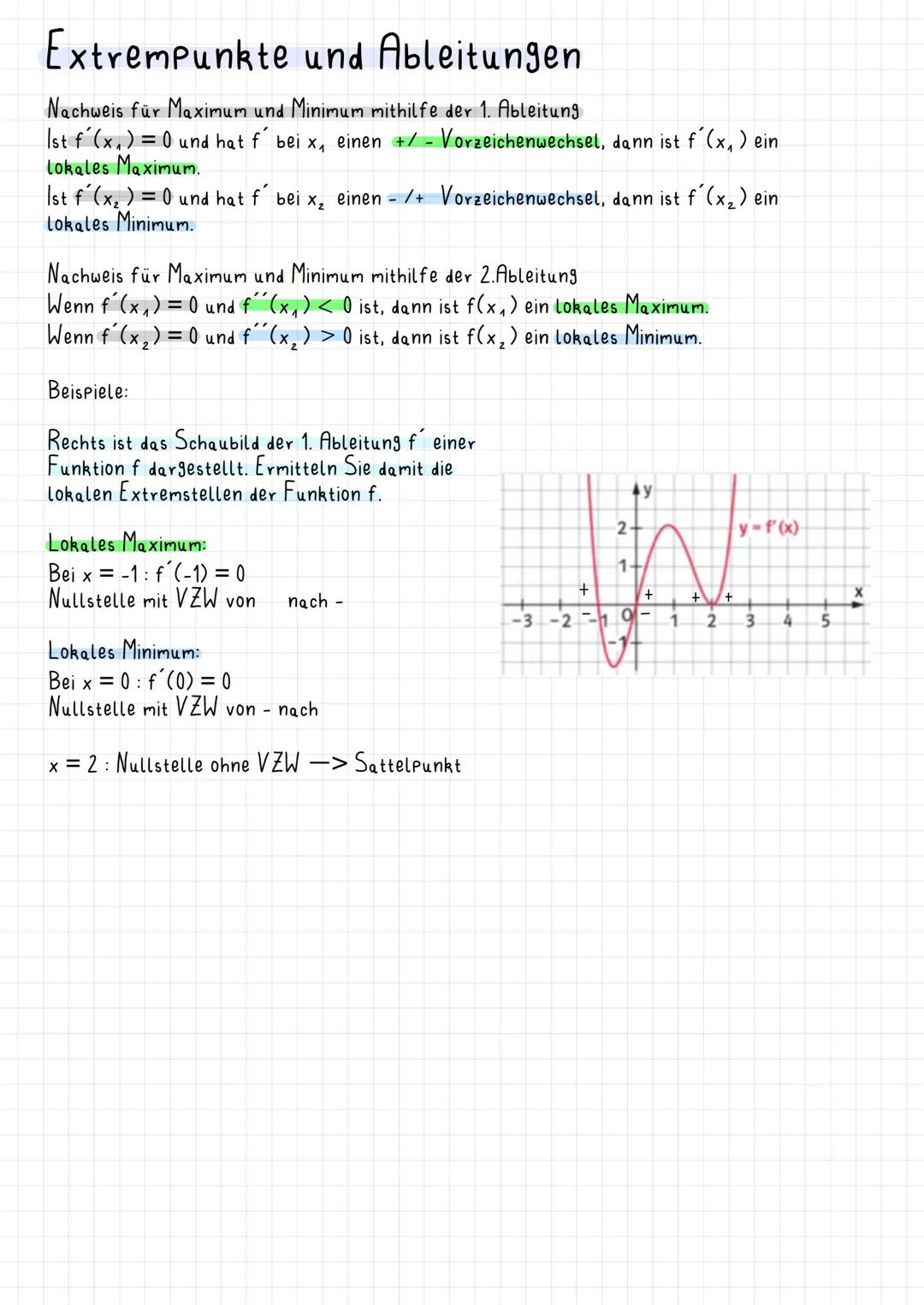
Methode 1 (Vorzeichenwechselkriterium): Wenn f'(x₁) = 0 ist und die erste Ableitung dabei das Vorzeichen wechselt, hast du einen Extrempunkt gefunden. Wechsel von + zu - bedeutet Maximum, von - zu + bedeutet Minimum.

Methode 2 (Zweite Ableitung): Noch schneller geht's mit f''$x$: Ist f'(x₁) = 0 und f''(x₁) < 0, dann Maximum. Ist f'(x₂) = 0 und f''(x₂) > 0, dann Minimum. Easy!

Vorsicht vor Sattelpunkten: Wenn f'$x$ = 0 ist, aber kein Vorzeichenwechsel stattfindet, hast du keinen Extrempunkt erwischt.

Eselsbrücke: Bei der zweiten Ableitung denk an ein Lächeln (> 0 = Minimum) und an ein trauriges Gesicht (< 0 = Maximum).

Krümmung, 2. Ableitung, Wendepunkte

Die zweite Ableitung verrät dir nicht nur Extrempunkte, sondern auch, wie sich die Funktion "biegt"! Linksgekrümmt (f''$x$ > 0) bedeutet, die Kurve öffnet sich nach oben wie eine Schüssel. Rechtsgekrümmt (f''$x$ < 0) heißt, sie öffnet sich nach unten.

Wendepunkte sind die Stellen, wo die Krümmung wechselt – von links- zu rechtsgekrümmt oder umgekehrt. Bedingung: f''(x₀) = 0 und f'''(x₀) ≠ 0. Die Wendetangente ist besonders interessant, weil sie das Schaubild im Wendepunkt "durchsticht".

Im Beispiel siehst du die komplette Rechnung: f$x$ = 2x³ + 3x² + x führt zum Wendepunkt W$-½|0$ mit der Wendetangente y = -½x - ¼. Erst ableiten, dann f''$x$ = 0 setzen, dann prüfen!

Rechentrick: Vergiss nie die dritte Ableitung zu checken – nur wenn f'''(x₀) ≠ 0 ist, hast du wirklich einen Wendepunkt!