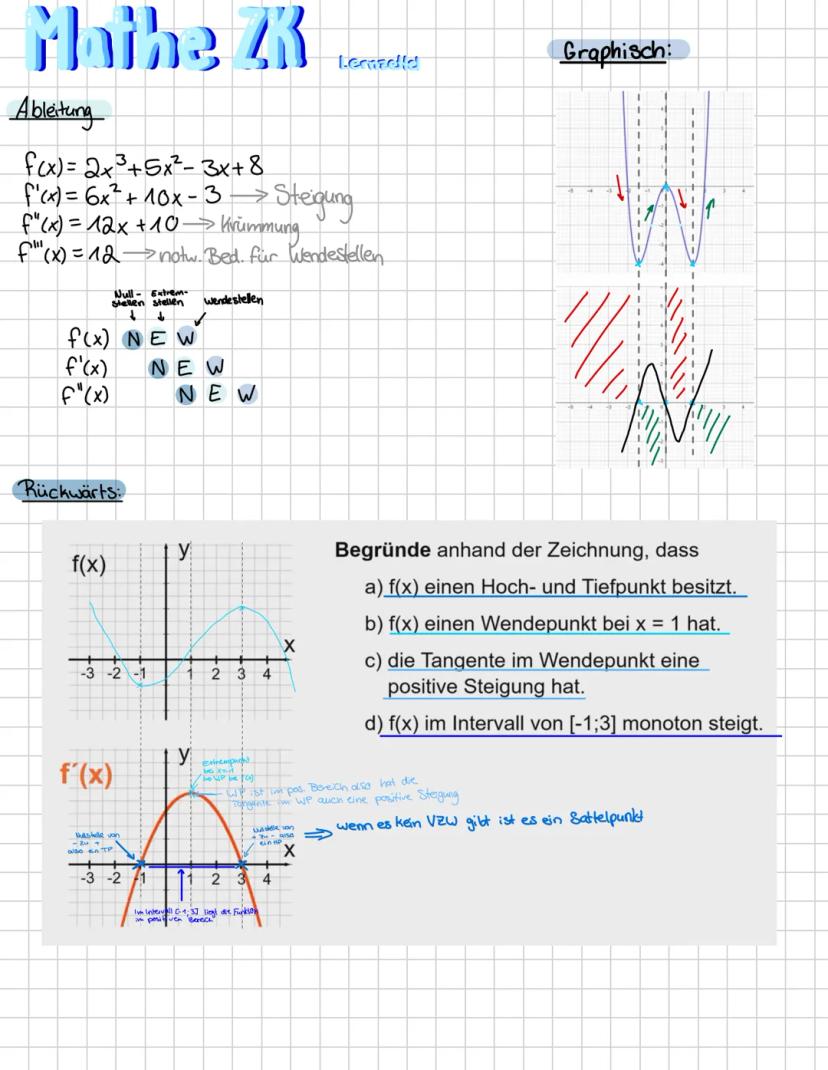
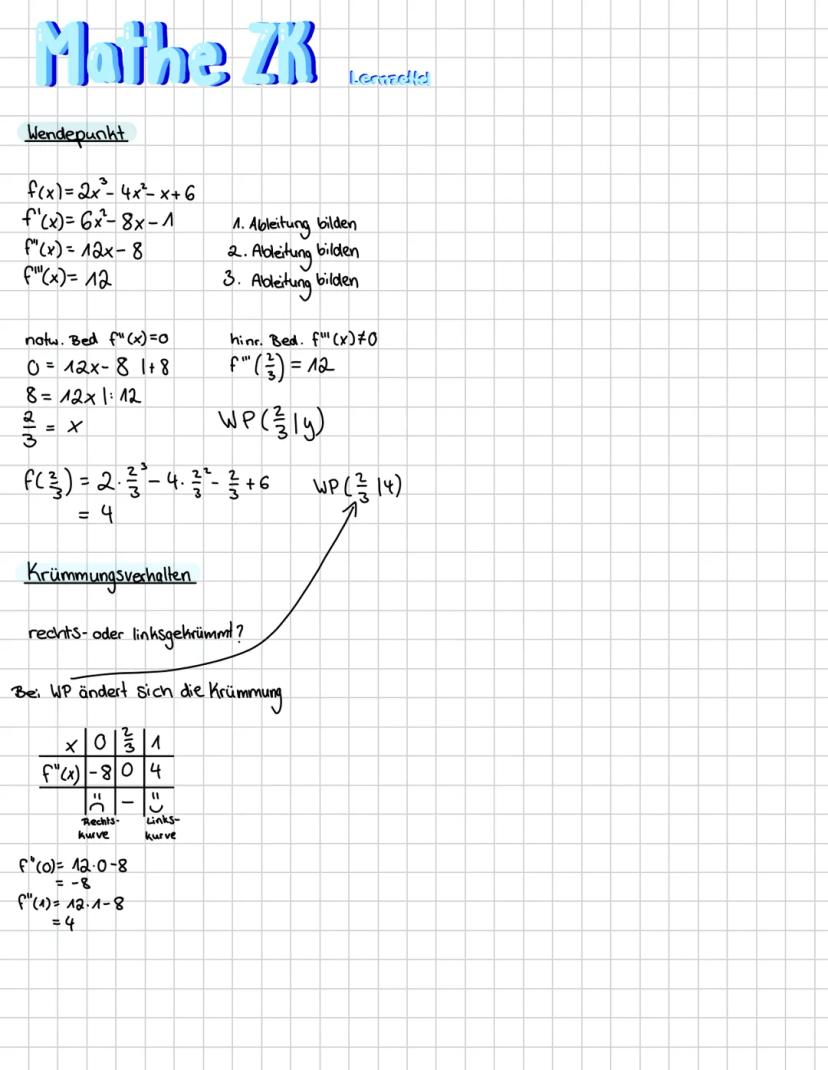
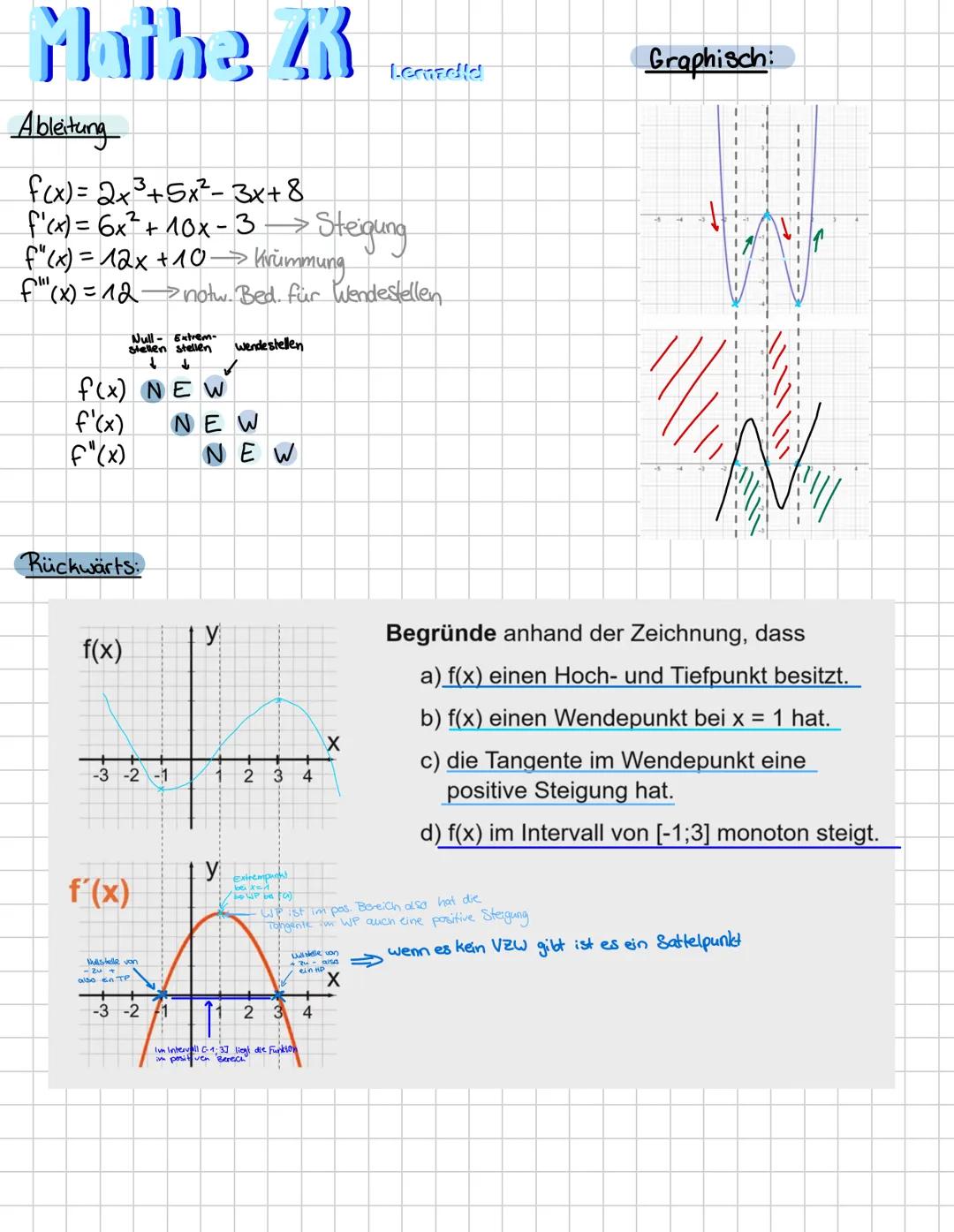
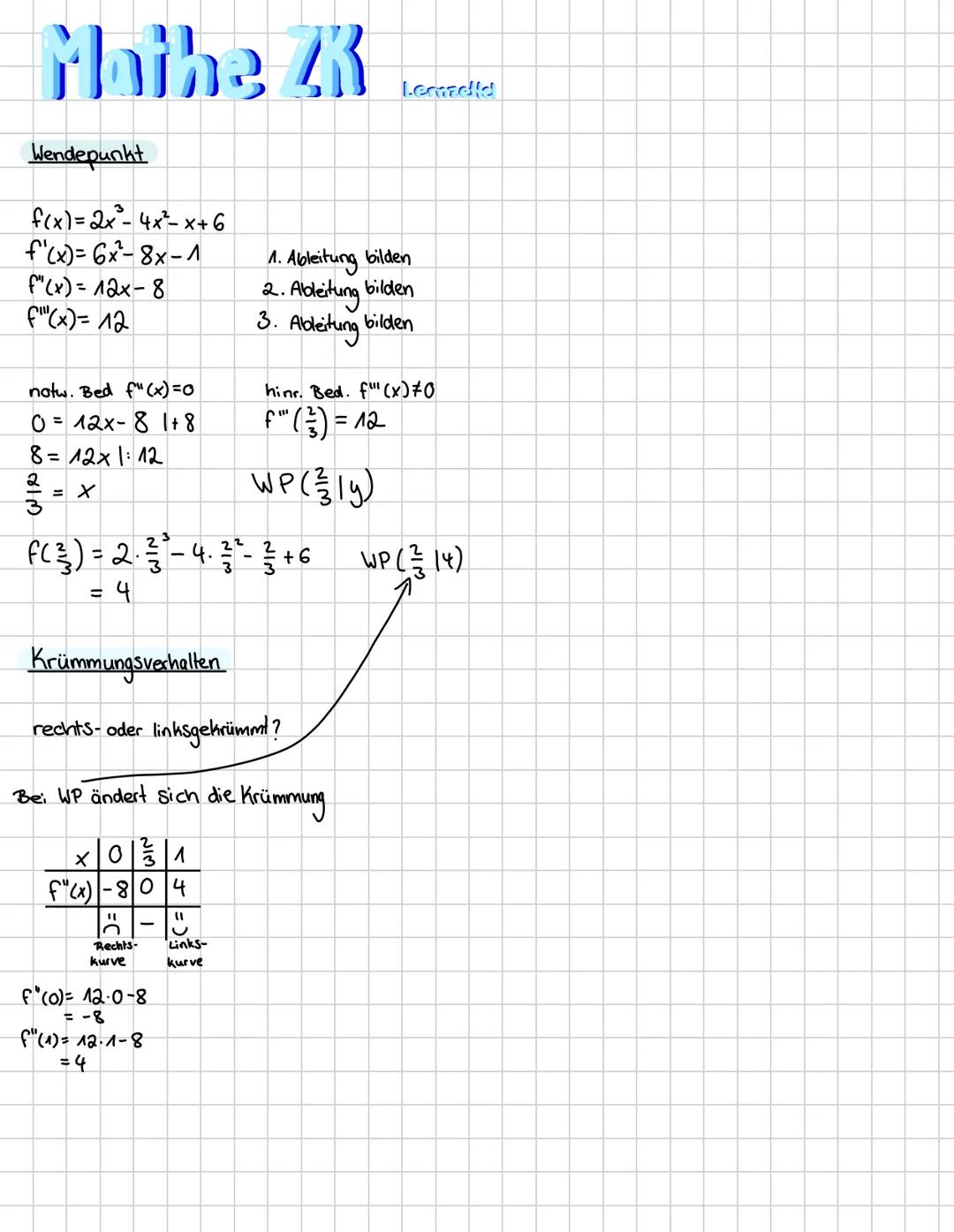
Funktionen in der Analysis

Potenzfunktionen wie f(x) = ax^n bestimmen viele wichtige Kurvenverläufe. Bei geraden Exponenten (x², x⁴, x⁶) entstehen achsensymmetrische Graphen, während ungerade Exponenten (x³, x⁵, x⁷) punktsymmetrische Graphen erzeugen.

Jede Funktion hat einen Definitionsbereich $mögliche x-Werte$ und einen Wertebereich $resultierende y-Werte$. Bei der Symmetrieuntersuchung hilft dir die Faustformel: Sind alle Exponenten ungerade und ohne normale Zahl ohne x, dann ist die Funktion punktsymmetrisch (UPS). Sind alle Exponenten gerade, ist die Funktion achsensymmetrisch zur y-Achse (GAS).

Das Grenzwertverhalten (Limes) beschreibt, was mit der Funktion passiert, wenn x sehr groß oder klein wird. Schau dir dafür den höchsten Exponenten und dessen Vorzeichen an - das verrät dir, ob die Funktion gegen +∞, -∞ oder einen festen Wert strebt.

⚡ Praxistipp: Um schnell herauszufinden, wie sich eine Funktion für sehr große x-Werte verhält, konzentriere dich nur auf den Term mit dem höchsten Exponenten - die anderen Terme werden vergleichsweise unbedeutend!

Vektoren und analytische Geometrie

Vektoren sind gerichtete Größen mit Länge und Richtung. Sie werden als Zahlenspalten dargestellt, wobei jede Komponente die Ausdehnung in eine bestimmte Richtung angibt. Die Länge eines Vektors berechnest du mit dem Satz des Pythagoras: |v| = √$v₁² + v₂² + ...$.

Du kannst Vektoren addieren, subtrahieren oder mit Skalaren multiplizieren. Der Verbindungsvektor zwischen zwei Punkten ist einfach ihre Differenz. Besonders wichtig: Wenn du prüfen willst, ob zwei Vektoren kollinear (parallel) sind, musst du schauen, ob ihre Komponenten proportional zueinander sind.

Das Skalarprodukt zweier Vektoren berechnest du, indem du die entsprechenden Komponenten multiplizierst und dann summierst. Ein Skalarprodukt von 0 bedeutet, dass die Vektoren senkrecht zueinander stehen.

🔍 Beachte: Wenn du einen Vektor mit -1 multiplizierst, erhältst du seinen Gegenvektor, der in die entgegengesetzte Richtung zeigt. Das ist praktisch für viele geometrische Berechnungen!

Differentialrechnung: Änderungsraten

Die mittlere Änderungsrate (Differenzenquotient) gibt die durchschnittliche Steigung zwischen zwei Punkten an: m = $y₂-y₁$/$x₂-x₁$. Sie ist die Grundlage für viele Berechnungen in Physik und Wirtschaft.

Die momentane Änderungsrate ist die Steigung der Tangente an einem bestimmten Punkt. Du berechnest sie durch die erste Ableitung der Funktion. Bei f(x) = x² ist die Ableitung f'(x) = 2x, sodass die Steigung bei x=3 genau f'(3) = 2·3 = 6 beträgt.

Mit der h-Methode kannst du Ableitungen ohne Ableitungsregeln herleiten. Dabei nutzt du den Grenzwert: lim(h→0) $f(x₀+h)-f(x₀)$/h. Dies führt oft zu längeren Rechnungen, liefert aber wichtige Einsichten in den Differentiationsprozess.

🧠 Verstehe es so: Die Ableitung ist wie eine Momentaufnahme der Geschwindigkeit. Während der Differenzenquotient dir die Durchschnittsgeschwindigkeit auf einer Strecke gibt, zeigt dir die Ableitung genau, wie schnell sich der Funktionswert an einem bestimmten Punkt ändert.

Ableitungen und Wendestellen

Die Ableitung einer Funktion gibt dir wichtige Informationen über ihr Verhalten. Bei f(x) = 2x³+5x²-3x+8 ist f'(x) = 6x²+10x-3 die erste Ableitung (Steigung) und f''(x) = 12x+10 die zweite Ableitung (Krümmung).

Nullstellen der ersten Ableitung sind potentielle Extremstellen $Hoch- oder Tiefpunkte$. Nullstellen der zweiten Ableitung sind potentielle Wendestellen, an denen sich die Krümmungsrichtung ändert.

Anhand des Graphen der Ableitung f'(x) kannst du viel über die Originalfunktion f(x) erkennen:

• Wo f'(x) positiv ist, steigt f(x)
• Wo f'(x) negativ ist, fällt f(x)
• Wo f'(x) = 0 ist, hat f(x) eine waagerechte Tangente

📊 Grafische Analyse: Wenn du den Graphen der Ableitung vor dir hast, zeigen die Schnittpunkte mit der x-Achse die Extremstellen der Originalfunktion an. Positive Bereiche der Ableitung bedeuten, dass die Originalfunktion dort steigt.

Transformation von Funktionen

Mit Transformationen kannst du Funktionsgraphen verändern und anpassen. Für f(x) = 3x²+4x+2 bedeutet:

• f(x) + a: Verschiebung um a Einheiten nach oben
• f(x) - a: Verschiebung um a Einheiten nach unten
• f$x+a$: Verschiebung um a Einheiten nach links
• f$x-a$: Verschiebung um a Einheiten nach rechts

Auch die Form des Graphen kannst du ändern:

• a·f(x) mit a>1: Streckung in y-Richtung um Faktor a
• f(a·x) mit a>1: Stauchung in x-Richtung um Faktor a
• -f(x): Spiegelung an der x-Achse
• f$-x$: Spiegelung an der y-Achse

Das Monotonieverhalten einer Funktion gibt an, ob sie steigt oder fällt. Eine Funktion ist streng monoton steigend, wenn ihre Steigung überall positiv ist, und streng monoton fallend, wenn die Steigung überall negativ ist.

🔄 Merkhilfe: Für Verschiebungen gilt: Was im Funktionsterm bei x steht, wirkt in die entgegengesetzte Richtung auf der x-Achse. Bei f$x+3$ wird der Graph um 3 nach links verschoben!

Kurvendiskussion und Extremstellen

Bei der Kurvendiskussion unterscheidest du zwischen lokalen und globalen Extrempunkten. Lokale Extrempunkte sind Hoch- oder Tiefpunkte in einem bestimmten Bereich, während globale Extrempunkte die absolut höchsten oder tiefsten Punkte der gesamten Funktion sind.

Um Extremstellen zu berechnen, nutzt du die notwendige Bedingung f'(x) = 0. Für f(x) = (2/3)x³+3x²+4x bildest du also zunächst die Ableitung f'(x) = 2x²+6x+4 und setzt diese gleich Null. Durch Lösen der quadratischen Gleichung erhältst du die potenziellen Extremstellen.

Zur Überprüfung, ob es sich um Hoch- oder Tiefpunkte handelt, gibt es zwei Methoden:

1. Vorzeichenwechsel-Kriterium: Untersuche, ob die erste Ableitung ihr Vorzeichen wechselt
2. Zweite Ableitung: Ist f''(x) an der Stelle negativ, handelt es sich um einen Hochpunkt; ist sie positiv, um einen Tiefpunkt

📝 Prüfungstipp: In Klausuren solltest du immer beide Werte berechnen: sowohl die x-Koordinate als auch den zugehörigen Funktionswert y = f(x). Nur dann hast du die vollständigen Koordinaten des Extrempunkts!

Wendepunkte und Krümmungsverhalten

Wendepunkte sind Stellen, an denen eine Funktion ihre Krümmungsrichtung ändert - von linksgekrümmt zu rechtsgekrümmt oder umgekehrt. Für f(x) = 2x³-4x²-x+6 findest du den Wendepunkt, indem du:

1. Die zweite Ableitung f''(x) = 12x-8 bildest
2. Diese gleich Null setzt: 12x-8 = 0
3. Nach x auflöst: x = 2/3
4. Den y-Wert berechnest: f(2/3) = 4

Die hinreichende Bedingung für einen Wendepunkt ist, dass die dritte Ableitung an dieser Stelle ungleich Null ist. In diesem Fall ist f'''(x) = 12, also immer erfüllt.

Das Krümmungsverhalten einer Funktion wird durch das Vorzeichen der zweiten Ableitung bestimmt:

• f''(x) < 0: linksgekrümmt (Graph öffnet sich nach unten)
• f''(x) > 0: rechtsgekrümmt (Graph öffnet sich nach oben)

↪️ Anwendungsbeispiel: Wendepunkte spielen in der Physik eine wichtige Rolle, z.B. beim Beschleunigungswechsel. Auch in der Wirtschaft markieren sie oft den Punkt, an dem sich Wachstumsraten ändern.