Änderungsraten und ihre Anwendungen
Die mittlere Änderungsrate beschreibt die durchschnittliche Steigung zwischen zwei Punkten. Die Formel lautet: f(x2)−f(x1)/x2−x1. Bei P(2|-3) und Q(5|-4,5) ergibt das (-4,5-(-3))/(5-2) = -0,5.
In praktischen Aufgaben wie der Regentonne berechnest du: Δy/Δx = (6,4 - 4,4)/(15 - 0) ≈ 0,133 Liter pro Minute. Das zeigt die mittlere Volumenänderung.
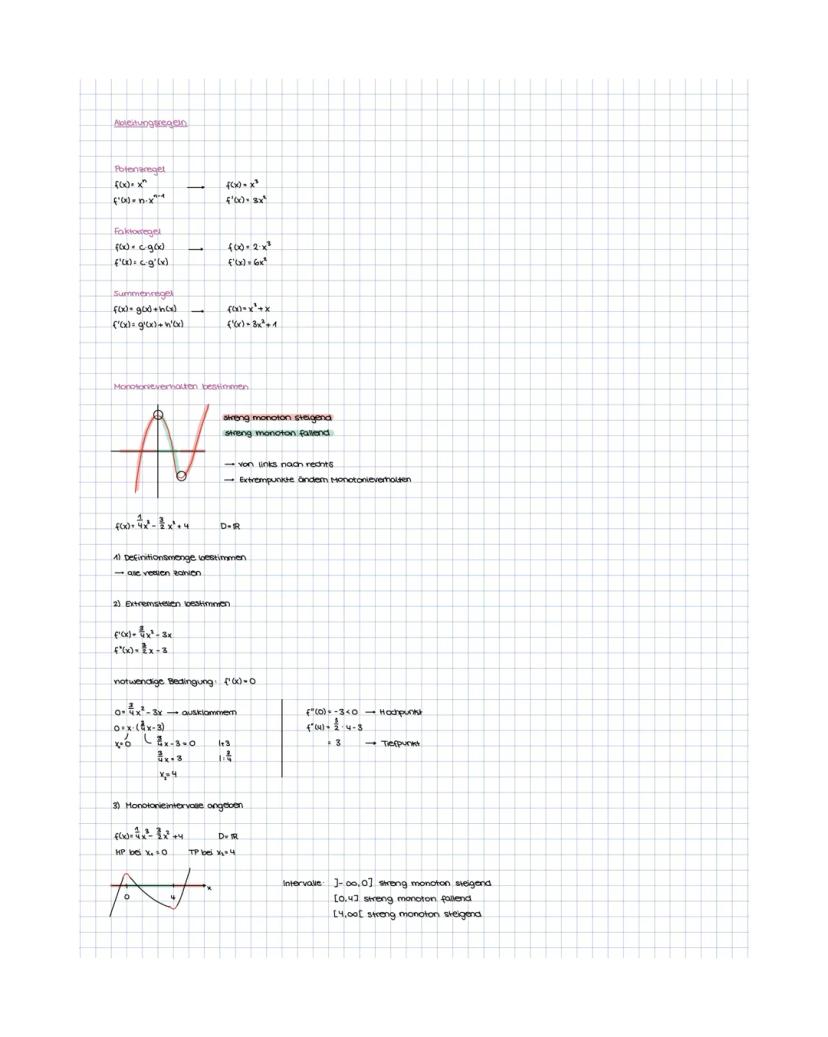
Die lokale Änderungsrate ist die Ableitung f'(x) an einem bestimmten Punkt. Sie gibt die momentane Steigung an - wie steil die Tangente dort verläuft.
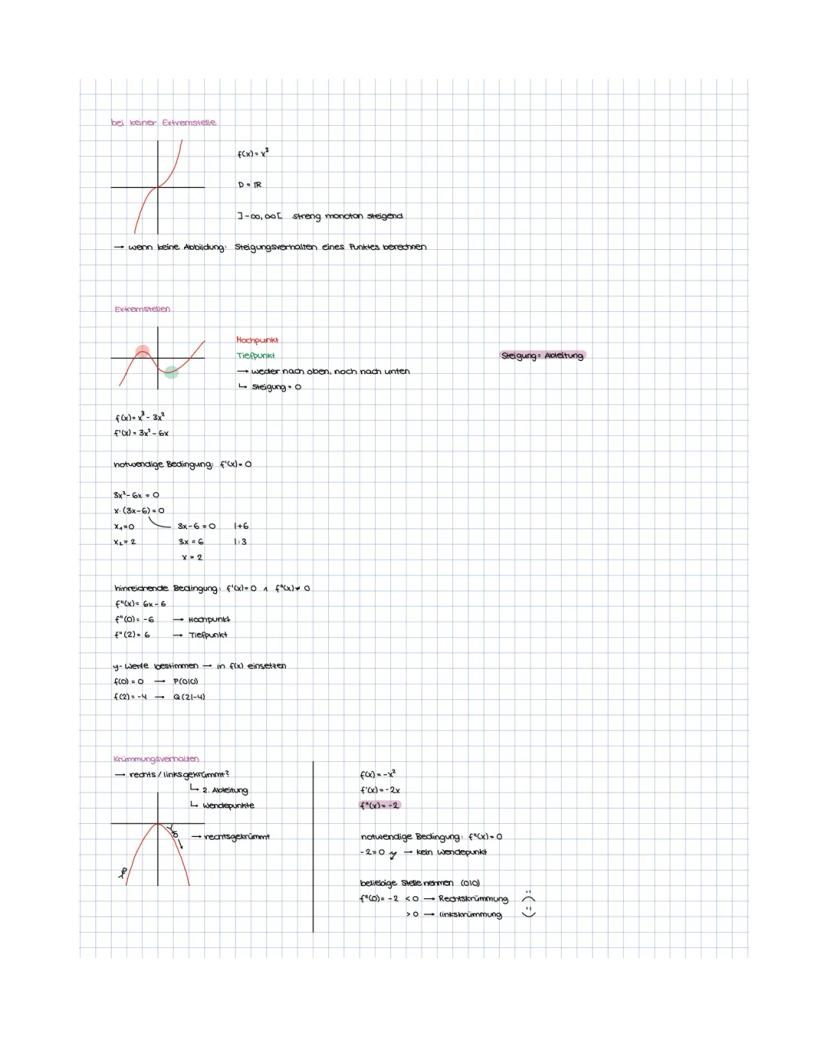
Der Zusammenhang zwischen Funktion und Ableitung ist wichtig: Hat f(x) ein Maximum, hat f'(x) eine Nullstelle mit Vorzeichenwechsel von + zu -.
Alltagsbezug: Die mittlere Geschwindigkeit im Auto entspricht der mittleren Änderungsrate - der Tacho zeigt die lokale!





![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_1.webp&w=2048&q=75)
![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_2.webp&w=2048&q=75)
![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_3.webp&w=2048&q=75)
![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_4.webp&w=2048&q=75)
![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_5.webp&w=2048&q=75)
![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_6.webp&w=2048&q=75)
![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_7.webp&w=2048&q=75)
![# ZK MATHE
Potenzfunktionen mit ganzzahligen Exponenten
| gerade | ungerade |
|---|---|
| 2,4,6... | 3,5,7... |
positiv | [graph1] | [](/_next/image?url=https%3A%2F%2Fcontent-eu-central-1.knowunity.com%2FCONTENT%2F01975496-ce2a-7c05-b216-03c53ed61fa5_image_page_8.webp&w=2048&q=75)