Loslegen

Mathematik

Geometrische Linienpostulate

Parallelenaxiom

Mathe2.583Aktualisiert 31. Aug. 20266 Seiten

Mathe Lernzettel Zentrale Klausur EPH 2025

Melden
user profile picture
Ally 🕯️@sunnyally
Zu Google-Quellen hinzufügen
Potenzfunktionen und Vektoren sind zwei zentrale Themen der Oberstufen-Mathematik, die dir in der 11. Klasse begegnen. Während Potenzfunktionen verschiedene charakteristische Verläufe zeigen und durch Ableitungen analysiert werden können, helfen dir Vektoren dabei, Punkte und Bewegungen im dreidimensionalen Raum zu beschreiben.
Mathe ZK 2025 – Seite 1

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

Potenzfunktionen verstehen

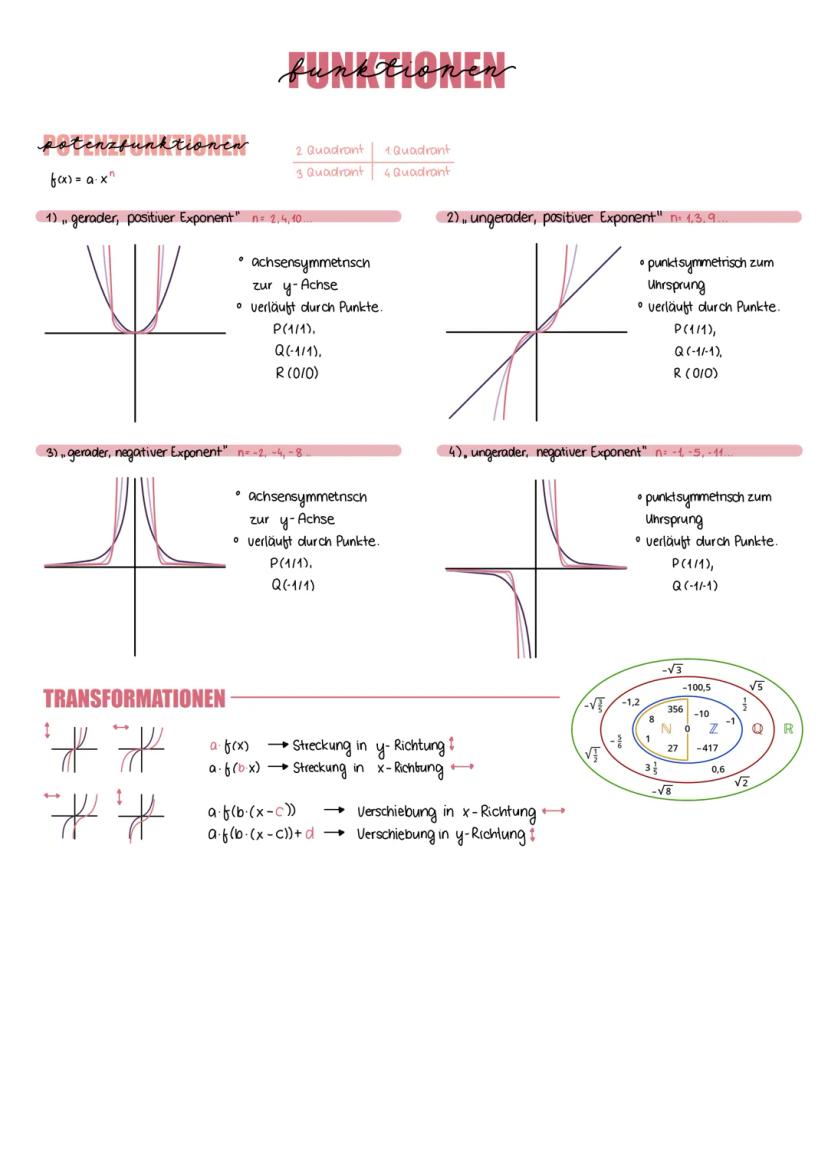
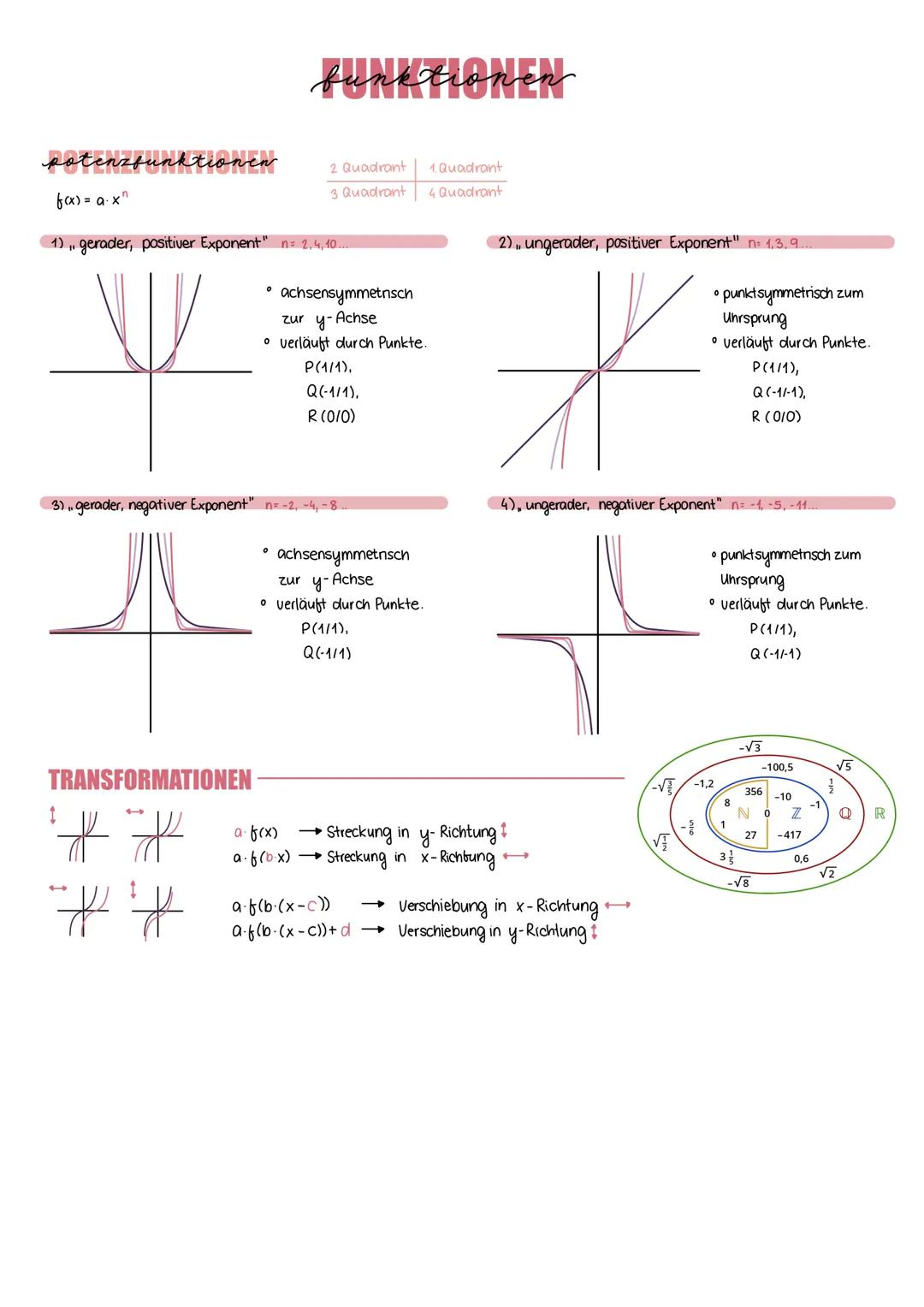
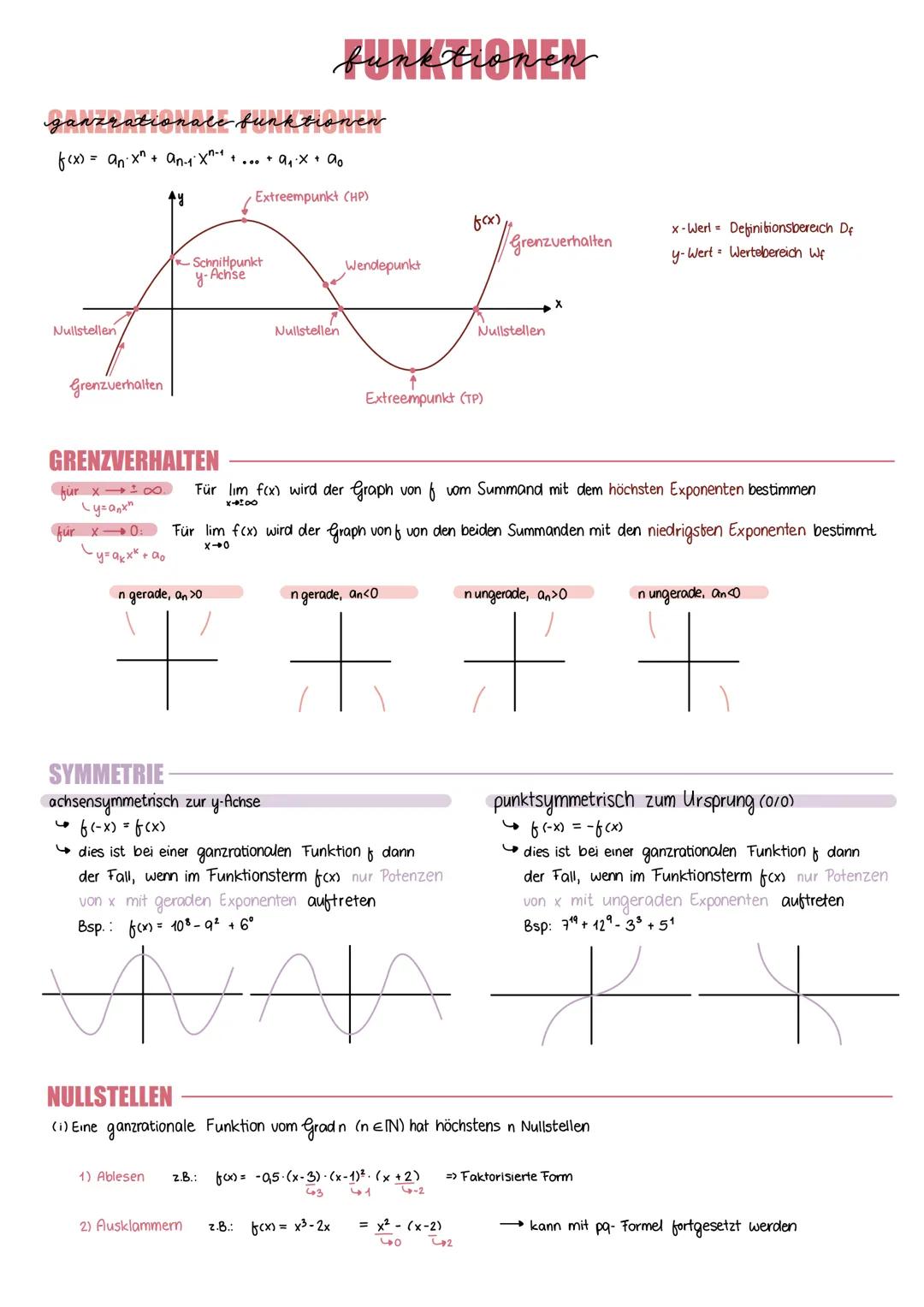
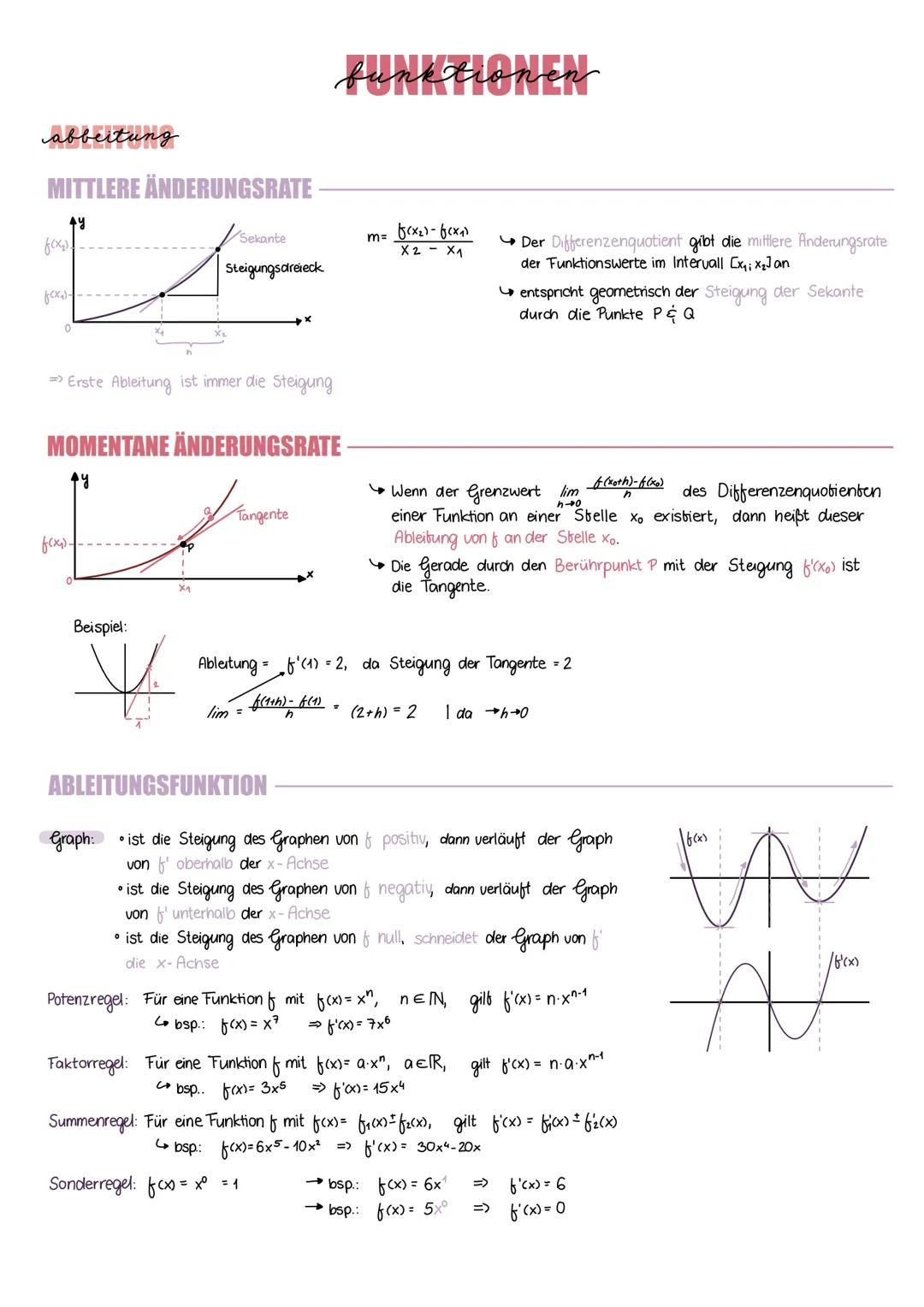
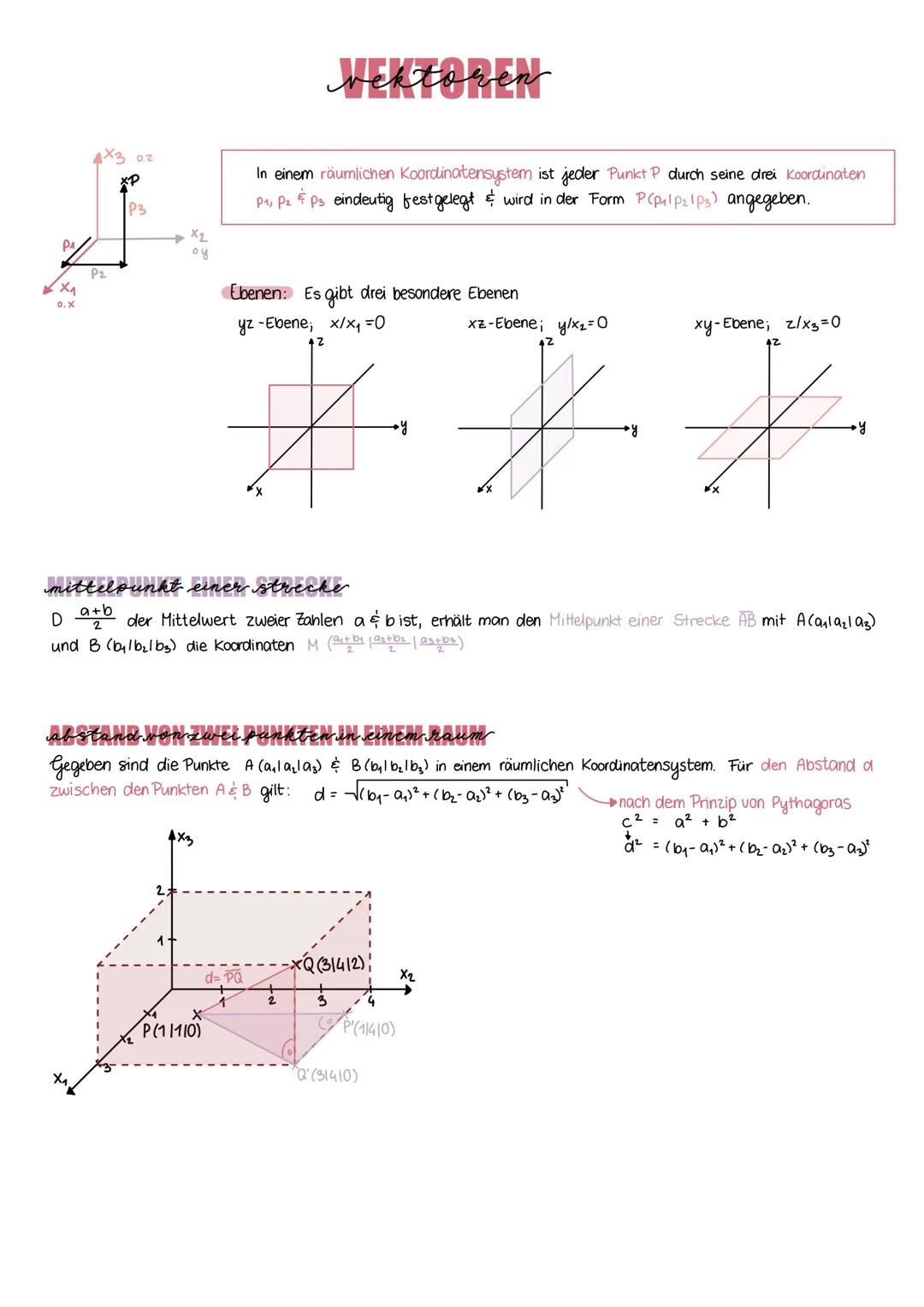
Potenzfunktionen der Form fxx = axⁿ verhalten sich je nach Exponent völlig unterschiedlich - und das ist eigentlich ziemlich logisch! Bei geradem, positivem Exponenten n=2,4,10n = 2, 4, 10 entstehen U-förmige Kurven, die achsensymmetrisch zur y-Achse sind.

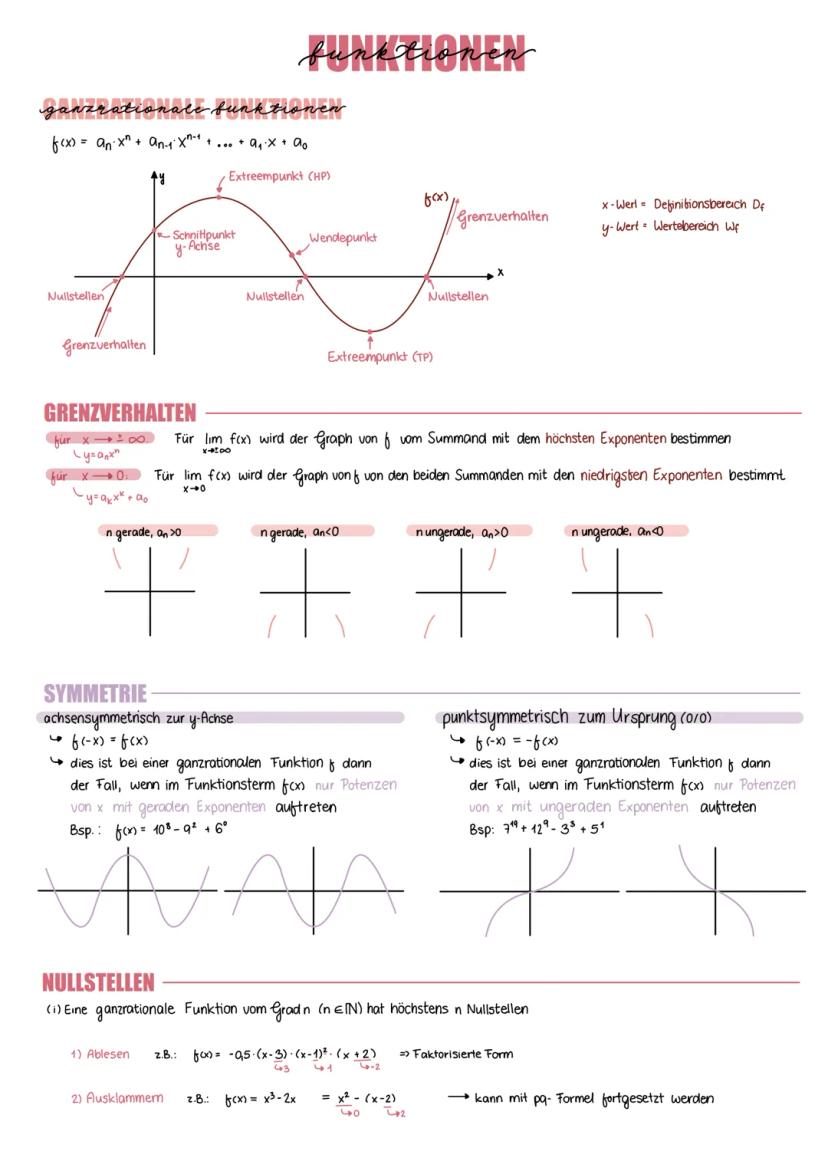
Ungerade, positive Exponenten n=1,3,9n = 1, 3, 9 erzeugen dagegen punktsymmetrische Funktionen zum Ursprung - sie sehen aus wie gestreckte S-Kurven. Beide Typen verlaufen durch die charakteristischen Punkte P(1|1) und R(0|0).

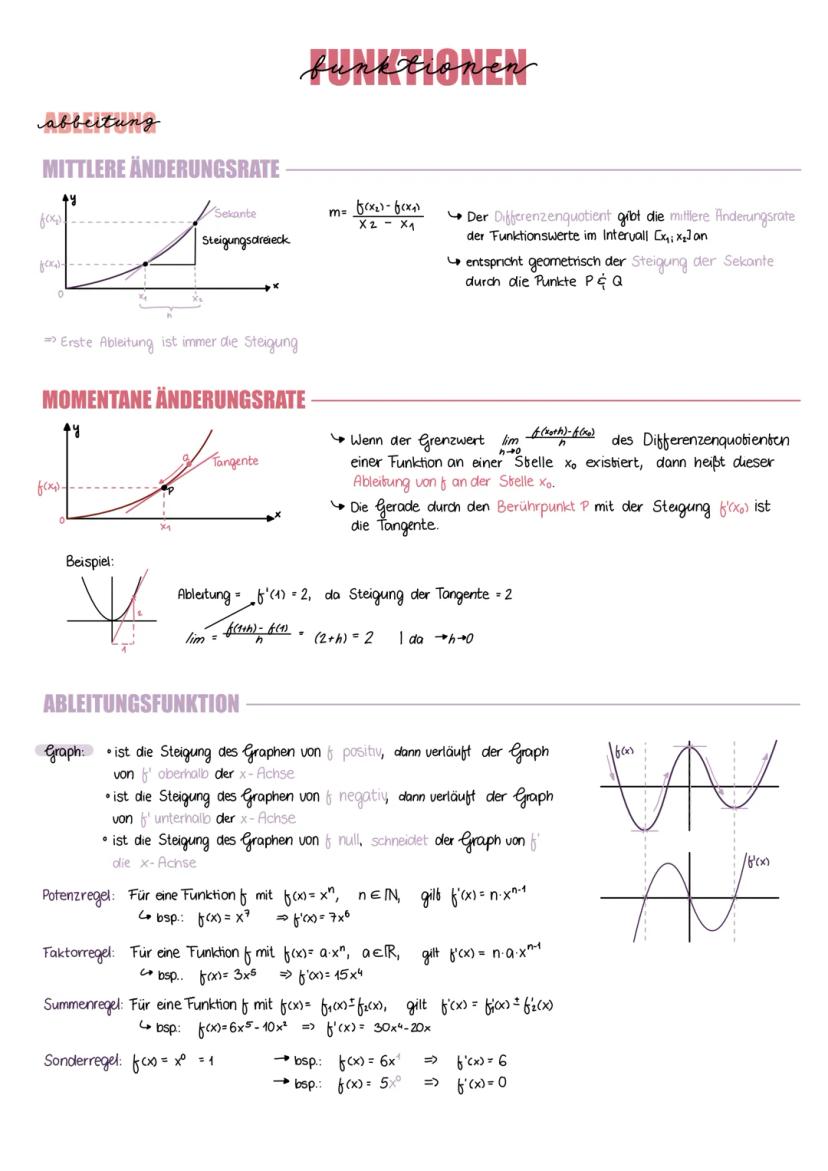
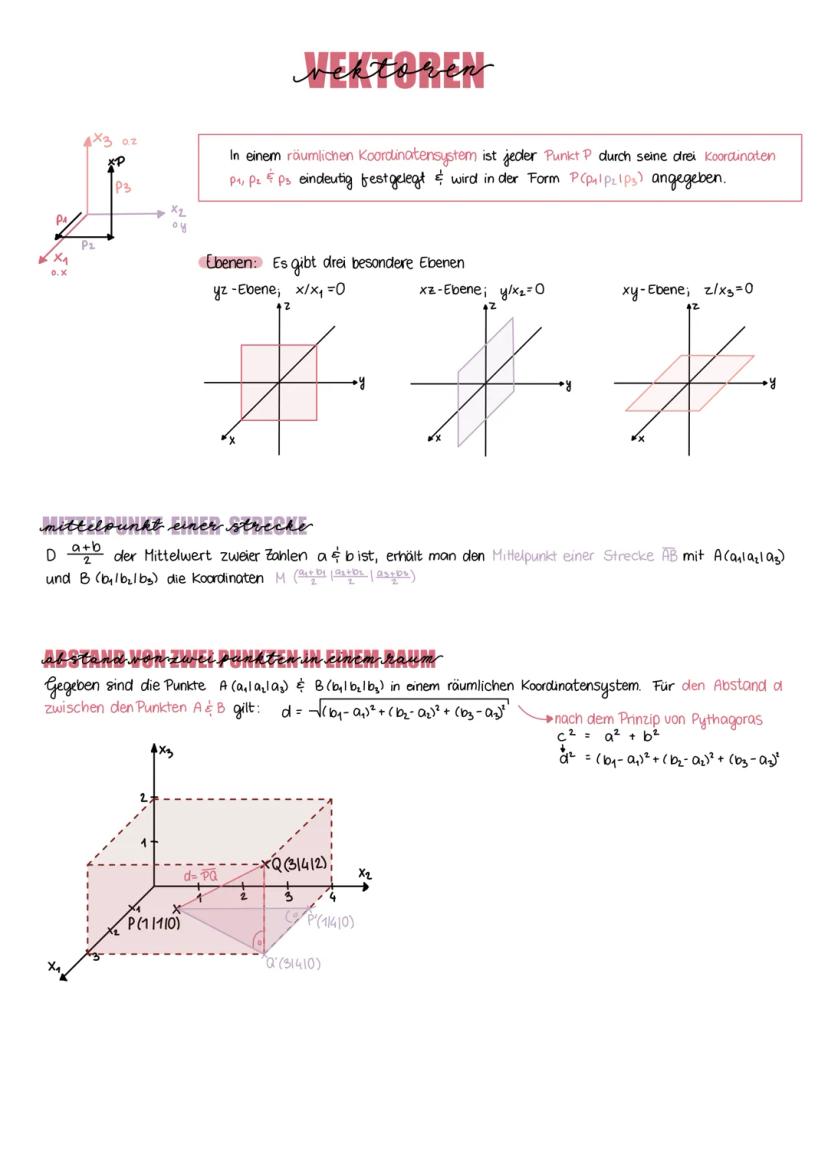
Bei negativen Exponenten wird's interessant: Die Funktionen haben Definitionslücken und nähern sich den Achsen an, ohne sie zu berühren. Auch hier gilt: gerade Exponenten → achsensymmetrisch, ungerade Exponenten → punktsymmetrisch.

💡 Merktipp: Gerade Exponenten = symmetrisch zur y-Achse, ungerade Exponenten = symmetrisch zum Ursprung!

Transformationen verschieben und strecken diese Grundfunktionen: Der Parameter a streckt in y-Richtung, b in x-Richtung, c verschiebt horizontal und d vertikal.

Mathe ZK 2025 – Seite 2

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

Ganzrationale Funktionen analysieren

Ganzrationale Funktionen sind wie die großen Geschwister der Potenzfunktionen - sie kombinieren verschiedene Potenzen zu einer Funktion. Die allgemeine Form fxx = aₙxⁿ + aₙ₋₁x^n−1n-1 + ... + a₁x + a₀ sieht kompliziert aus, folgt aber klaren Regeln.

Das Grenzverhalten wird immer vom Term mit dem höchsten Exponenten bestimmt - alle anderen werden bei sehr großen x-Werten unwichtig. Bei geradem höchstem Exponenten gehen beide Äste in dieselbe Richtung, bei ungeradem in entgegengesetzte Richtungen.

Symmetrie erkennst du sofort am Funktionsterm: Nur gerade Exponenten → achsensymmetrisch zur y-Achse. Nur ungerade Exponenten → punktsymmetrisch zum Ursprung. Gemischte Exponenten → keine Symmetrie.

💡 Prüfungstipp: Eine Funktion vom Grad n hat höchstens n Nullstellen - das ist immer eine beliebte Klausurfrage!

Nullstellen findest du durch Faktorisieren, Ausklammern oder die pq-Formel. In faktorisierter Form kannst du sie direkt ablesen.

Mathe ZK 2025 – Seite 3

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

Ableitungen meistern

Die Ableitung ist dein Werkzeug, um herauszufinden, wie steil eine Funktion an jedem Punkt verläuft. Die mittlere Änderungsrate zwischen zwei Punkten entspricht der Steigung der Sekante - das kennst du schon aus der Mittelstufe.

Viel spannender ist die momentane Änderungsrate: Sie gibt die exakte Steigung an einem einzigen Punkt an und entspricht der Steigung der Tangente. Mathematisch ist das der Grenzwert des Differenzenquotienten.

Die Ableitungsregeln sind deine besten Freunde: Potenzregel (xⁿ wird zu n·x^n−1n-1), Faktorregel (Konstanten bleiben als Faktor stehen) und Summenregel (jeden Term einzeln ableiten). Bei fxx = x ist die Ableitung immer 1, bei konstanten Funktionen immer 0.

💡 Visualisierungstipp: Ist f'xx positiv, steigt fxx an. Ist f'xx negativ, fällt fxx. Ist f'xx = 0, hat fxx einen waagerechten Punkt!

Potenzregel-Beispiel: fxx = x⁷ → f'xx = 7x⁶. Der Exponent wandert nach vorn, dann wird er um 1 verringert.

Mathe ZK 2025 – Seite 4

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

Kurvenuntersuchung komplett

Tangenten berechnen ist ein Dreischritt: Erst den y-Wert des Berührpunkts bestimmen, dann die Steigung über f'(x₀) berechnen, schließlich die Geradengleichung aufstellen. Die Normale steht senkrecht zur Tangente, ihre Steigung ist der negative Kehrwert.

Extrempunkte findest du systematisch: f'xx = 0 setzen (notwendige Bedingung), dann f''xx bilden und prüfen (hinreichende Bedingung). Ist f''(x₀) > 0, hast du ein Minimum. Ist f''(x₀) < 0, ein Maximum.

Die Monotonie liest du direkt an f'xx ab: Ist die erste Ableitung positiv, steigt die Funktion. Ist sie negativ, fällt sie. So einfach ist das!

💡 Klausur-Hack: Lerne die pq-Formel und die binomischen Formeln auswendig - die brauchst du ständig beim Lösen von f'xx = 0!

Wendepunkte erfordern die dritte Ableitung: f''xx = 0 (notwendige Bedingung) und f'''(x₀) ≠ 0 (hinreichende Bedingung). Das Krümmungsverhalten erkennst du an f''xx: positiv = linksgekrümmt (Lächeln), negativ = rechtsgekrümmt (Trauer).

Mathe ZK 2025 – Seite 5

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

Punkte im Raum verstehen

Der dreidimensionale Raum erweitert dein bisheriges Koordinatensystem um eine dritte Achse - jetzt brauchst du drei Koordinaten P(x|y|z) für jeden Punkt. Die drei Grundebenen xy-, xz- und yz-Ebene teilen den Raum in acht Bereiche.

Den Mittelpunkt einer Strecke berechnest du wie gewohnt: Alle Koordinaten der Endpunkte addieren und durch 2 teilen. Bei A(1|2|3) und B(5|4|7) ist M also (1+5)/2∣(2+4)/2∣(3+7)/2(1+5)/2 | (2+4)/2 | (3+7)/2 = M(3|3|5).

Abstände zwischen Punkten berechnest du mit der erweiterten Pythagorras-Formel: d = √(x2−x1)2+(y2−y1)2+(z2−z1)2(x₂-x₁)² + (y₂-y₁)² + (z₂-z₁)². Das ist logisch - du berechnest einfach die Diagonale eines dreidimensionalen Quaders.

💡 Vorstellungshilfe: Stell dir vor, du willst von einem Punkt zum anderen - erst gehst du in x-Richtung, dann in y-Richtung, dann in z-Richtung. Der direkte Weg ist die Diagonale!

Die Berechnung funktioniert genauso wie im zweidimensionalen Fall, nur mit einer zusätzlichen Koordinate.

Mathe ZK 2025 – Seite 6

Melde dich an, um den Inhalt zu sehen.
Kostenlos!

Vektoren rechnen und verstehen

Vektoren sind Verschiebungen im Raum - stell sie dir wie Pfeile vor, die eine Richtung und eine Länge haben. Sie werden durch drei Komponenten beschrieben und mit kleinen Buchstaben bezeichnet. Der Nullvektor verschiebt gar nichts, der Gegenvektor verschiebt in die entgegengesetzte Richtung.

Ortsvektoren zeigen vom Ursprung zu einem bestimmten Punkt - sie sind wie Wegbeschreibungen vom Koordinatenursprung aus. Einen Vektor von Punkt A zu Punkt B berechnest du durch "Ziel minus Start": Die x-Koordinate von B minus die von A, und so weiter.

Der Betrag eines Vektors ist seine Länge und wird mit der Formel |v⃗| = √v12+v22+v32v₁² + v₂² + v₃² berechnet. Das ist wieder der gute alte Pythagoras, nur in drei Dimensionen!

💡 Rechenregel: Vektoraddition und -subtraktion funktioniert komponentenweise - einfach die entsprechenden Zahlen addieren oder subtrahieren!

Skalarmultiplikation streckt oder staucht Vektoren: Multiplizierst du mit 2, wird der Vektor doppelt so lang. Mit -1 drehst du ihn um. Kollineare Vektoren sind Vielfache voneinander - sie zeigen in dieselbe oder entgegengesetzte Richtung.

Wir dachten schon, du fragst nie...

Unser KI-Begleiter ist ein speziell für Schüler entwickeltes KI-Tool, das mehr als nur Antworten bietet. Basierend auf Millionen von Knowunity-Inhalten liefert er relevante Informationen, personalisierte Lernpläne, Quizze und Inhalte direkt im Chat und passt sich deinem individuellen Lernweg an.

Du kannst die App im Google Play Store und im Apple App Store herunterladen.

Genau! Genieße kostenlosen Zugang zu Lerninhalten, vernetze dich mit anderen Schülern und hol dir sofortige Hilfe – alles direkt auf deinem Handy.

Ähnlicher Inhalt

Mathe

Strahlensätze: Parallel und Nicht-Parallel

Entdecken Sie die Strahlensätze I und II, einschließlich der Anwendung auf parallele und nicht-parallele Linien. Diese Zusammenfassung bietet eine klare Erklärung der Konzepte und deren Bedeutung in der Geometrie. Ideal für Schüler, die sich auf Prüfungen vorbereiten oder ihr Verständnis vertiefen möchten.

91793
Mathe

Volumen von Rotationskörpern

Erfahren Sie, wie man das Volumen von Rotationskörpern berechnet, die um die x-Achse rotiert werden. Diese Zusammenfassung behandelt die Zerlegung in Zylinder, die Anwendung von Integralen und Beispiele zur Volumenberechnung. Ideal für Studierende der Integralrechnung und Mathematik. Typ: Zusammenfassung.

111.84771
Mathe

Rotationskörper: Volumenberechnung

Entdecken Sie die Grundlagen der Rotationskörper, einschließlich ihrer Definition, typischen Formen wie Zylinder und Kegel, sowie deren praktische Anwendungen. Lernen Sie, wie man das Volumen dieser geometrischen Figuren berechnet und testen Sie Ihr Wissen mit einer Beispielaufgabe. Ideal für Mathematik auf grundlegendes Niveau.

127705
Mathe

Definitionsbereich & Wertebereich

Erfahre alles über die Schreibweise von Definitions- und Wertebereichen in der Mathematik. Diese Zusammenfassung bietet klare Beispiele und Erklärungen zu Intervallschreibweisen, einschließlich offener und geschlossener Intervalle. Ideal für Studierende, die sich auf Prüfungen vorbereiten oder ihr Verständnis vertiefen möchten.

101.83318
Mathe

Zahlenmengen und Mengensymbole

Entdecken Sie die Grundlagen der Zahlenmengen, Mengenschreibweisen und Intervallschreibweisen. Diese Zusammenfassung behandelt auch logische Symbole und wichtige Brüche, einschließlich der Umwandlung von Brüchen und periodischen Dezimalzahlen. Ideal für Mathematikstudenten, die ihre Kenntnisse in Mengenlehre vertiefen möchten.

101.58039
Mathe

Volumen von Rotationskörpern

Erfahren Sie, wie man das Volumen von Rotationskörpern berechnet, einschließlich der allgemeinen Volumensformel und spezifischer Formeln für Kegel und Kugeln. Diese Zusammenfassung behandelt die Zerlegung in Zylinder und die Anwendung des Satzes von Pythagoras zur Bestimmung von Volumina. Ideal für Studierende der Geometrie und Analysis.

125158
Mehr anzeigen

Beliebtester Inhalt: Mathe

Mathe

Quantitative Probleme im TMS

Entdecken Sie Strategien zur Lösung quantitativer und formaler Probleme im Medizinertest. Dieser Leitfaden umfasst wichtige Formeln zur Prozentrechnung, Umrechnungen von Einheiten und die Eigenschaften von Lösungen. Ideal für Studierende, die sich auf den Medizinertest vorbereiten und ihre mathematischen Fähigkeiten verbessern möchten.

1120.238597
Mathe

Integralrechnung und Flächenberechnung

Erfahre alles über die Integralrechnung, einschließlich unbestimmter und bestimmter Integrale, Integralschreibweise und Rechenregeln. Lerne, wie man Flächeninhalte zwischen Funktionsgraphen berechnet und die Kurvendiskussion durchführt. Ideal für die Vorbereitung auf Klausuren in der Differential- und Integralrechnung.

1213.146336
Mathe

Stochastik Lernzettel Abitur

Übersicht zu allen Stochastik Themen für das Mathe Abitur (Bayern 2026), Hypothesentest fehlt

111.26723
Mathe

Geraden und Ebenen im Raum

Entdecken Sie die Grundlagen der analytischen Geometrie mit Fokus auf Vektoren, Geraden und Ebenen. Erfahren Sie mehr über Lagebeziehungen, Abstände, Winkel und Orthogonalität. Ideal für Studierende der Mathematik und Ingenieurwissenschaften. Diese Zusammenfassung bietet klare Erklärungen und Beispiele zur Vertiefung des Verständnisses.

113.69894
Mathe

Analysis: Funktionsscharen & Ableitungen

Dieser Lernzettel bietet eine umfassende Übersicht über zentrale Themen der Analysis, einschließlich Funktionsscharen, Ableitungen, Extrempunkte, Integrale und e-Funktionen. Ideal für die Vorbereitung auf das Abitur im Mathematik Grundkurs. Verstehe die Konzepte und deren Anwendungen mit klaren Beispielen und Schritt-für-Schritt-Anleitungen.

1113.708292
Mathe

Analysis und Kurvendiskussion

Entdecken Sie die Grundlagen der Analysis, einschließlich Funktionsarten, Differentialrechnung, Kurvendiskussion (Nullstellen, Extremstellen, Monotonie, Krümmung) und Integralrechnung (Flächeninhalte, Volumen von Rotationskörpern). Diese umfassende Zusammenfassung bietet auch Einblicke in Funktionsscharen und Extremwertaufgaben. Ideal für Studierende, die sich auf Prüfungen vorbereiten oder ihr Wissen vertiefen möchten.

112.63456
Mathe

Integrationsregeln und Anwendungen

Entdecken Sie die grundlegenden Rechenregeln für unbestimmte und bestimmte Integrale, einschließlich der Potenzregel, Summenregel und Substitutionsregel. Lernen Sie, wie man Stammfunktionen findet und die Fläche unter Graphen mit bestimmten Integralen berechnet. Ideal für Studierende der Mathematik und Ingenieurwissenschaften.

1141.1612.209
Mathe

Scheitelpunktform & Nullstellen

Erfahre alles über die Scheitelpunktform quadratischer Funktionen, wie man Nullstellen mit der p-q Formel findet und Schnittpunkte zwischen Parabeln ermittelt. Diese Zusammenfassung bietet klare Schritte zur Umformung und Analyse quadratischer Gleichungen, ideal für Schüler, die sich auf Prüfungen vorbereiten.

101.59224
Mathe

Mathe LK Abitur

Mathe Abitur 2024

131.55728

Beliebtester Inhalt

Deutsch

Heimsuchung Abitur 2026 Lernzettel

Alles über Heimsuchung, Kapitelzusaemfassung, Themen, Deutung, Figurenkonstellation und mögliche Streitfragen

128.250195
Deutsch

Abilernzettel Heimsuchung 2025

Figurenkonstellation, Kapitel Zusammenfassung, Charaktere, Motive, Deutungsansätze,

1149.9821.024
Lerntipps

Führerschein Theorie Wiederholung/Notizen

Schilder, Zeichen, Zahlen, Vorfahrt und mehr - alles für die theoretische Führerscheinprüfung :)

1010.847187
Deutsch

Heimsuchung_JennyErpenbeck_Abitur

Zusammenfassungen für jedes Kapitel, Analysen und Zitate

1217.374337
Deutsch

Heimsuchung komplette Zusammenfassung

Zusammenfassung des Buches als auch der einzelnen Kapitel und deren Charakteren. Auch tabellarisch. Im Unterricht ohne KI erstellt

128.617196
Lerntipps

Fahrschule Theorieprüfung Essentials

Entdecke die wichtigsten Punkte für die Theorieprüfung in der Fahrschule. Diese Zusammenfassung behandelt Geschwindigkeitsbegrenzungen, Sicherheitsabstände, Verkehrszeichen und wichtige Berechnungen für Reaktions- und Bremswege. Ideal für angehende Fahrer, die sich optimal vorbereiten möchten.

1179.1062.231
Deutsch

Kapitelzusammenfassung Heimsuchung Jenny Erpenbeck

Zusammenfassung jeder Kapitel, Deutungen und Erklärungen

1216.419197
Deutsch

Charaktere aus Heimsuchung von Jenny Erpenbeck

Mindmap, Allgemeines, Verlauf

1221.065344
Deutsch

Heimsuchung - Erpenbeck Kapitelzusammenfassung

Kapitelübersichten von Heimsuchung (Jenny Erpenbeck) mit Seitenanzahl, Kapitelname und Inhaltszusammenfassung

123.36458

Schüler lieben uns, und du auch.

4.6/5App Store
4.7/5Google Play
Stefan SiOS-Nutzer

Die App ist sehr einfach zu bedienen und gut gestaltet. Ich habe bisher alles gefunden, wonach ich gesucht habe, und konnte viel aus den Präsentationen lernen! Ich werde die App definitiv für ein Schulprojekt nutzen! Und natürlich hilft sie auch sehr als Inspiration.

Samantha KlichAndroid-Nutzerin

Diese App ist wirklich super. Es gibt so viele Lernzettel und Hilfen [...]. Mein Problemfach ist zum Beispiel Französisch und die App hat so viele Möglichkeiten zur Hilfe. Dank dieser App habe ich mich in Französisch verbessert. Ich würde sie jedem empfehlen.

AnnaiOS-Nutzerin

Wow, ich bin wirklich begeistert. Ich habe die App einfach mal ausprobiert, weil ich sie schon oft beworben gesehen habe und war absolut beeindruckt. Diese App ist DIE HILFE, die man für die Schule braucht und vor allem bietet sie so viele Dinge wie Übungen und Lernzettel, die mir persönlich SEHR geholfen haben.