Klausurstruktur und Bewertungskriterien

Die Mathematikklausur zur e-Funktion umfasst insgesamt 60 Punkte, wobei die Noteneinteilung von ungenügend (unter 20%) bis sehr gut (ab 90%) reicht. Bei der Bearbeitung ist es wichtig, auf ein bis zwei Nachkommastellen zu runden und bei Sachaufgaben vollständige Antwortsätze zu formulieren.

Für eine gute Bewertung solltest du ausreichend Rechenschritte zeigen, damit deine Vorgehensweise nachvollziehbar ist. Die Verwendung des Taschenrechners ist während der gesamten Klausur erlaubt.

Die Klausur verwendet bestimmte Operatoren, die dir klare Anweisungen geben, wie du eine Aufgabe bearbeiten sollst:

• Diskutieren: Kurvendiskussion mit allen Merkmalen durchführen
• Angeben: Ergebnis ohne Rechnung nennen
• Zeigen: Aussagen durch Rechnungen oder logische Schlüsse bestätigen
• Berechnen: Vollständigen Rechenweg angeben
• Bestimmen: Lösungsweg aufzeigen und Ergebnis durch Rechnung oder Erklärung herleiten

💡 Tipp: Achte besonders auf die verwendeten Operatoren in jeder Aufgabe - sie geben dir einen klaren Hinweis, was genau von dir erwartet wird!

Aufgabentypen zur e-Funktion

Die Klausur deckt drei wesentliche Bereiche ab, die typisch für das Thema e-Funktion sind:

Aufgabentyp 1 (10 P.): Ableiten verschiedener e-Funktionen, von einfachen Formen wie $f(x) = e^x$ bis zu komplexeren Ausdrücken mit Produkten wie $(1-x) \cdot e^{\frac{x}{2}}$ oder $(x + 2)^2 + e^x$. Hier musst du die Ableitungsregeln für e-Funktionen und die Produkt- bzw. Summenregel anwenden.

Aufgabentyp 2 (30 P.): Eine vollständige Kurvendiskussion von e-Funktionen wie $f(x) = (1-x) \cdot e^x$ und $g(x) = \frac{1}{2}e^{-2x}$. Hierbei sollst du Definitionsbereich, Wertebereich, Achsenschnittpunkte, Symmetrie, Extrempunkte, Wendepunkte und das Globalverhalten analysieren und den Graphen skizzieren.

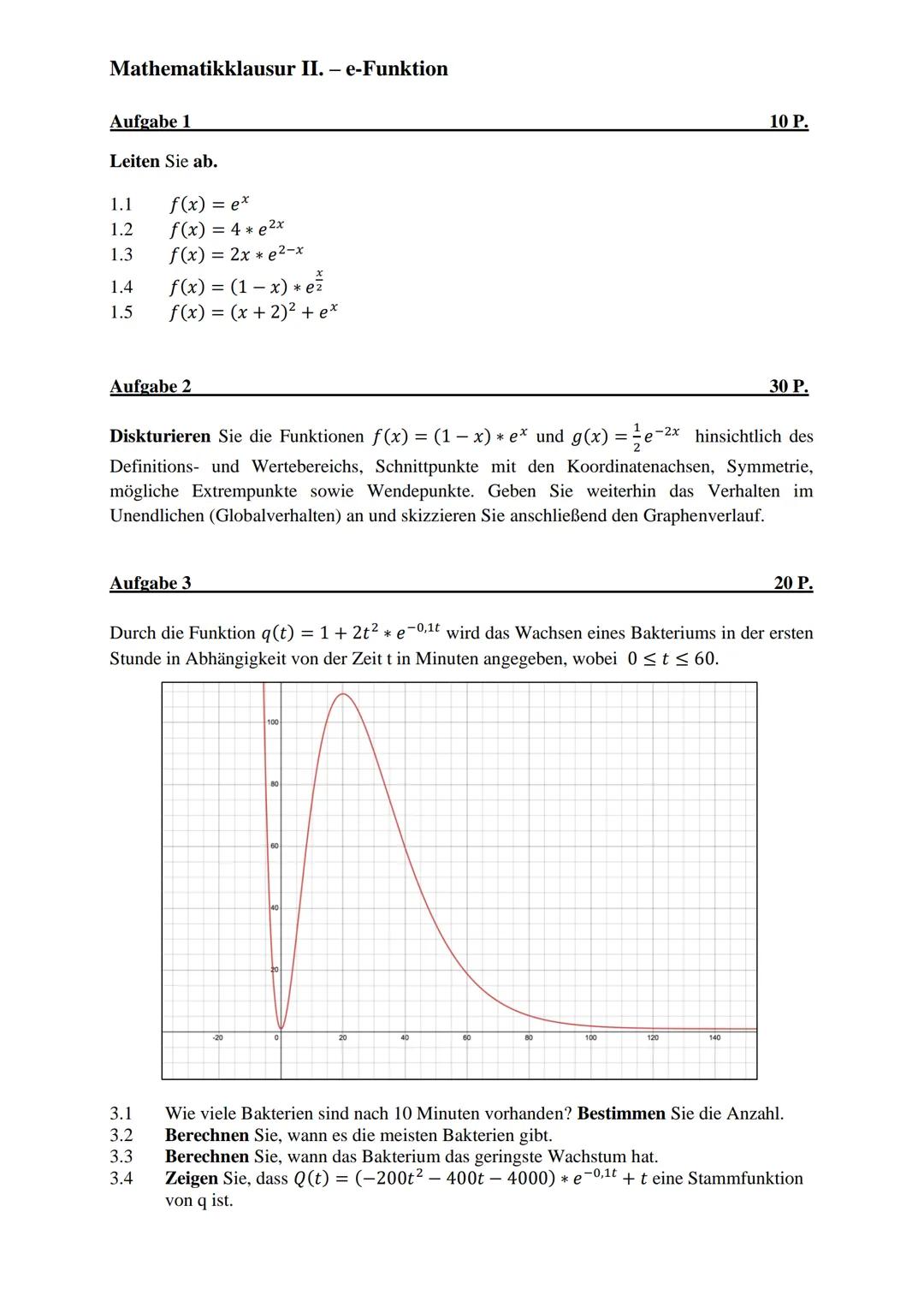
Aufgabentyp 3 (20 P.): Anwendungsaufgabe zum Bakterienwachstum mit der Funktion $q(t) = 1 + 2t^2 \cdot e^{-0.1t}$. Diese Aufgabe verlangt das Auswerten der Funktion zu bestimmten Zeitpunkten, das Bestimmen von Maxima und Minima sowie den Nachweis einer Stammfunktion.

💡 Praxistipp: Bei Kurvendiskussionen ist die systematische Vorgehensweise entscheidend - arbeite die Merkmale in der richtigen Reihenfolge ab und vergiss keine Eigenschaften!