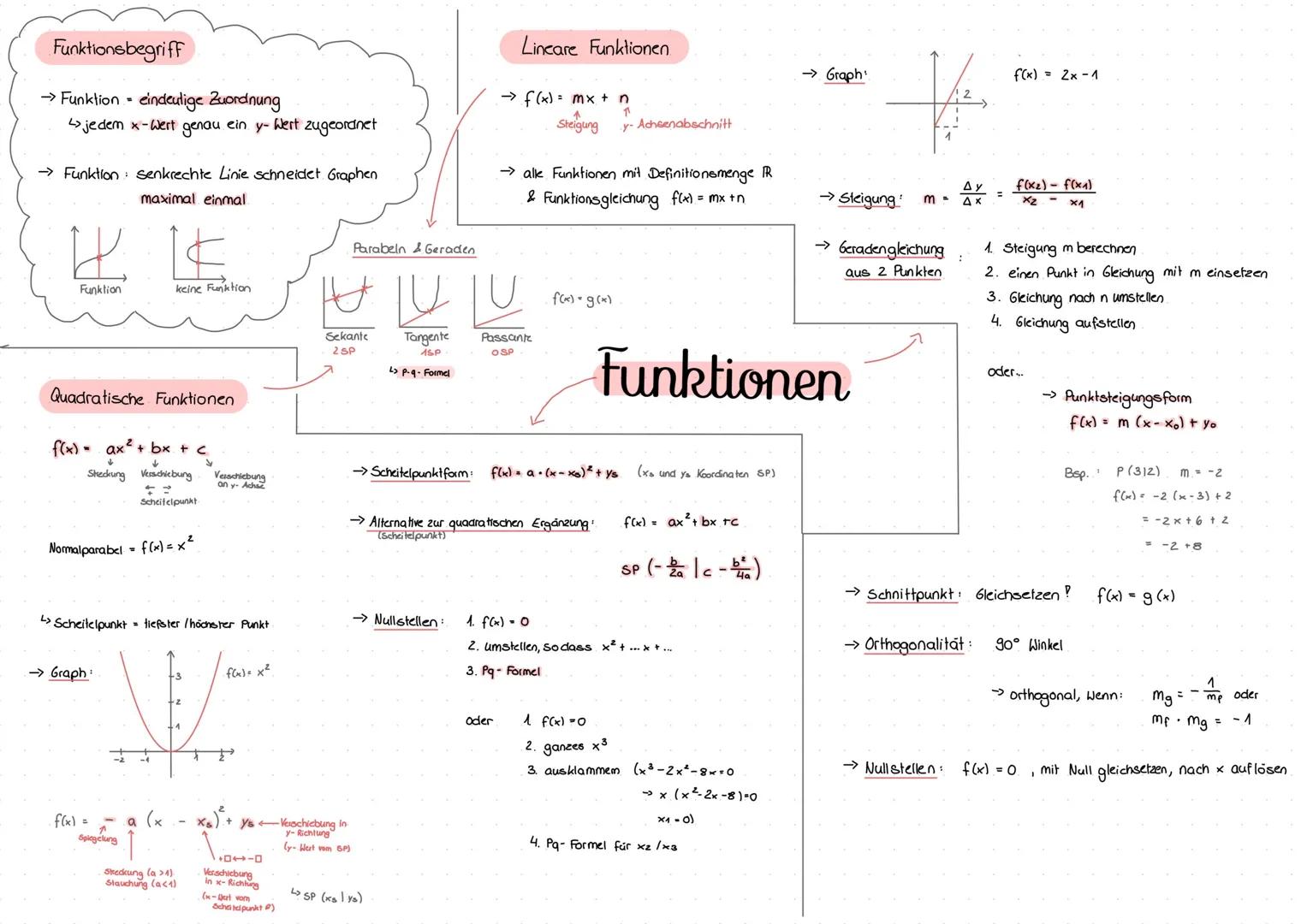
Funktionen verstehen - Parabeln & Geraden
Funktionen sind eindeutige Zuordnungen - das bedeutet, jedem x-Wert ist genau ein y-Wert zugeordnet. Ein einfacher Test: Wenn eine senkrechte Linie den Graphen maximal einmal schneidet, ist es eine Funktion.
Lineare Funktionen haben die Form f(x) = mx + n. Hier ist m die Steigung (wie steil die Gerade ist) und n der y-Achsenabschnitt wodieGeradediey−Achseschneidet. Die Steigung berechnest du mit m = Δy/Δx = f(x2)−f(x1)/x2−x1.
Quadratische Funktionen erkennst du an der Form f(x) = ax² + bx + c. Ihr Graph ist immer eine Parabel mit einem tiefsten oder höchsten Punkt - dem Scheitelpunkt. Die Normalparabel f(x) = x² ist dein Grundmodell.
💡 Merktipp: Lineare Funktionen = Geraden, quadratische Funktionen = Parabeln!
Nullstellen findest du, indem du f(x) = 0 setzt und nach x auflöst. Bei quadratischen Funktionen verwendest du die p-q-Formel oder klammerst geschickt aus.
Die Scheitelpunktform f(x) = ax−xs² + ys zeigt dir direkt den Scheitelpunkt S(xs|ys) und wie die Parabel verschoben oder gestreckt ist. Ist a > 1, wird gestreckt; ist 0 < a < 1, wird gestaucht.