Grundlagen der Polynomfunktionen
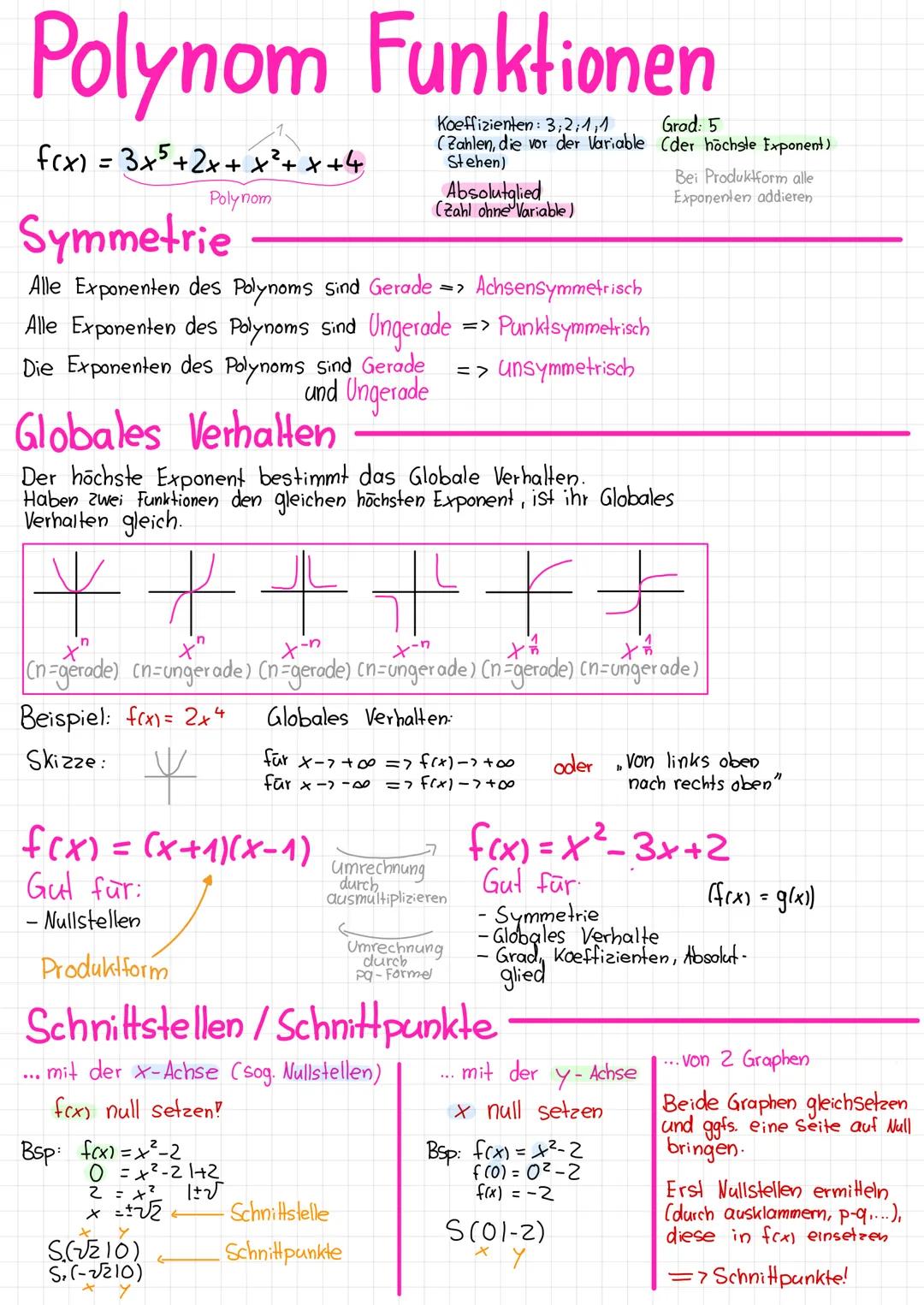
Polynome sind im Grunde nur Sammlungen von Termen mit verschiedenen Potenzen. Bei f(x) = 3x⁵+2x⁴+x²+x+4 siehst du alle wichtigen Teile: Die Koeffizienten (3, 2, 1, 1) stehen vor den Variablen, der Grad ist 5 (höchste Potenz), und das Absolutglied ist 4.
Die Symmetrie erkennst du an den Exponenten: Sind alle gerade → achsensymmetrisch, alle ungerade → punktsymmetrisch, gemischt → unsymmetrisch. Das globale Verhalten wird nur vom höchsten Exponenten bestimmt – bei x⁴ geht der Graph immer von oben nach oben.
Merke dir: Der höchste Exponent entscheidet, wie sich die Funktion im Unendlichen verhält!
Schnittpunkte findest du so: Mit der x-Achse → f(x) = 0 setzen (Nullstellen), mit der y-Achse → x = 0 einsetzen, zwischen zwei Graphen → gleichsetzen.