Quadratische Funktionen - Die drei Gesichter einer Parabel
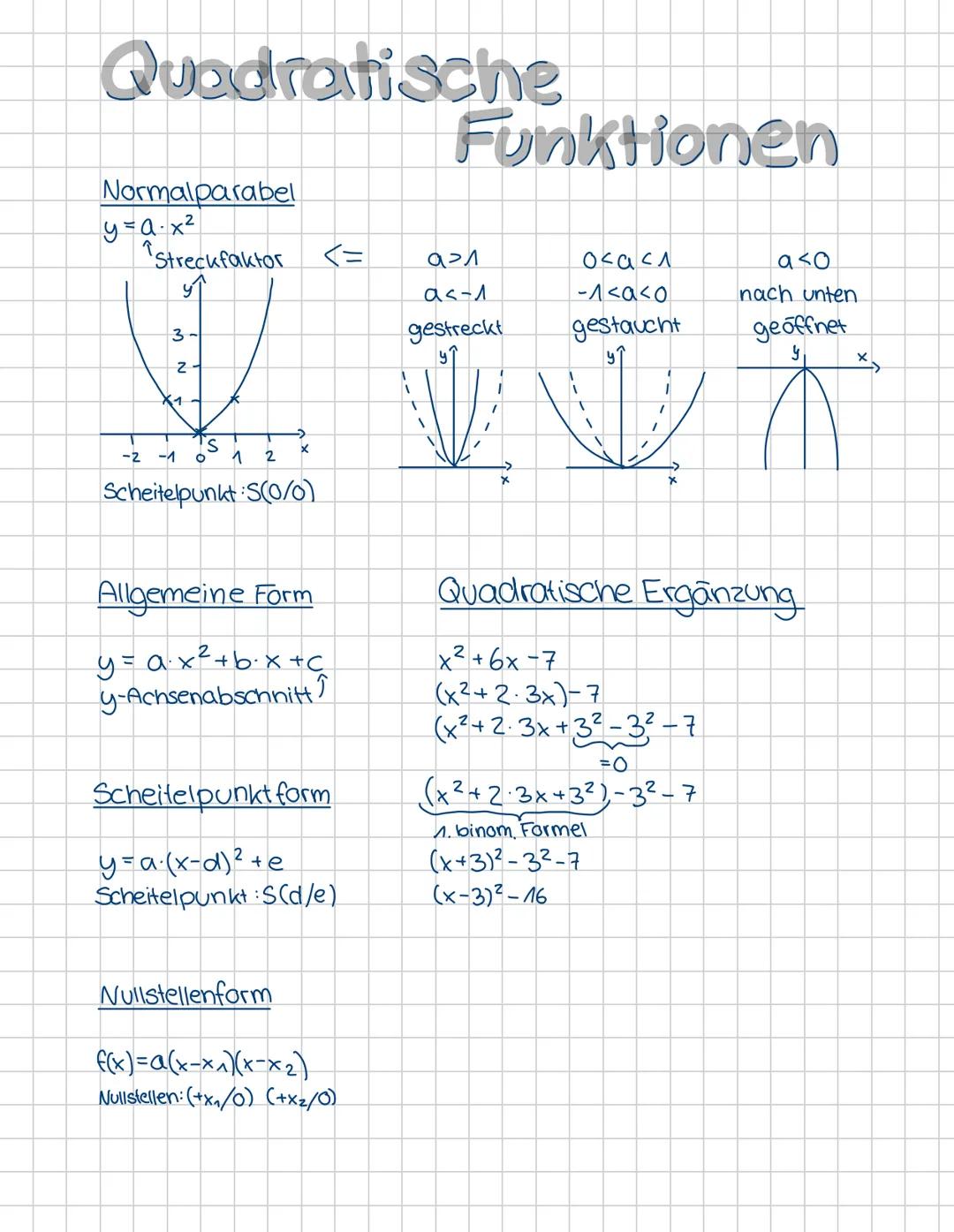
Stell dir vor, eine quadratische Funktion ist wie ein Chamäleon - sie kann ihr Aussehen ändern, bleibt aber immer dieselbe Funktion. Die Normalparabel y = x² ist dein Ausgangspunkt mit dem Scheitelpunkt S(0/0).
Der Streckfaktor a bestimmt, wie deine Parabel aussieht. Ist a > 1, wird sie gestreckt und steiler. Bei 0 < a < 1 wird sie gestaucht und flacher. Negative Werte drehen sie komplett um - dann öffnet sie sich nach unten.
Die allgemeine Form y = ax² + bx + c zeigt dir sofort den y-Achsenabschnitt (das ist c). Die Scheitelpunktform y = ax−d² + e verrät dir direkt den Scheitelpunkt Sd/e. Die Nullstellenform f(x) = ax−x1x−x2 macht die Nullstellen x₁ und x₂ sofort sichtbar.
Merktipp: Jede Form hat ihre Stärke - wähle die Form, die dir die Information gibt, die du gerade brauchst!
Mit der quadratischen Ergänzung kannst du elegant von der allgemeinen Form zur Scheitelpunktform wechseln. Das Beispiel x² + 6x - 7 wird zu x+3² - 16 - so siehst du sofort den Scheitelpunkt bei (-3/-16).