Quadratische Funktionen verstehen
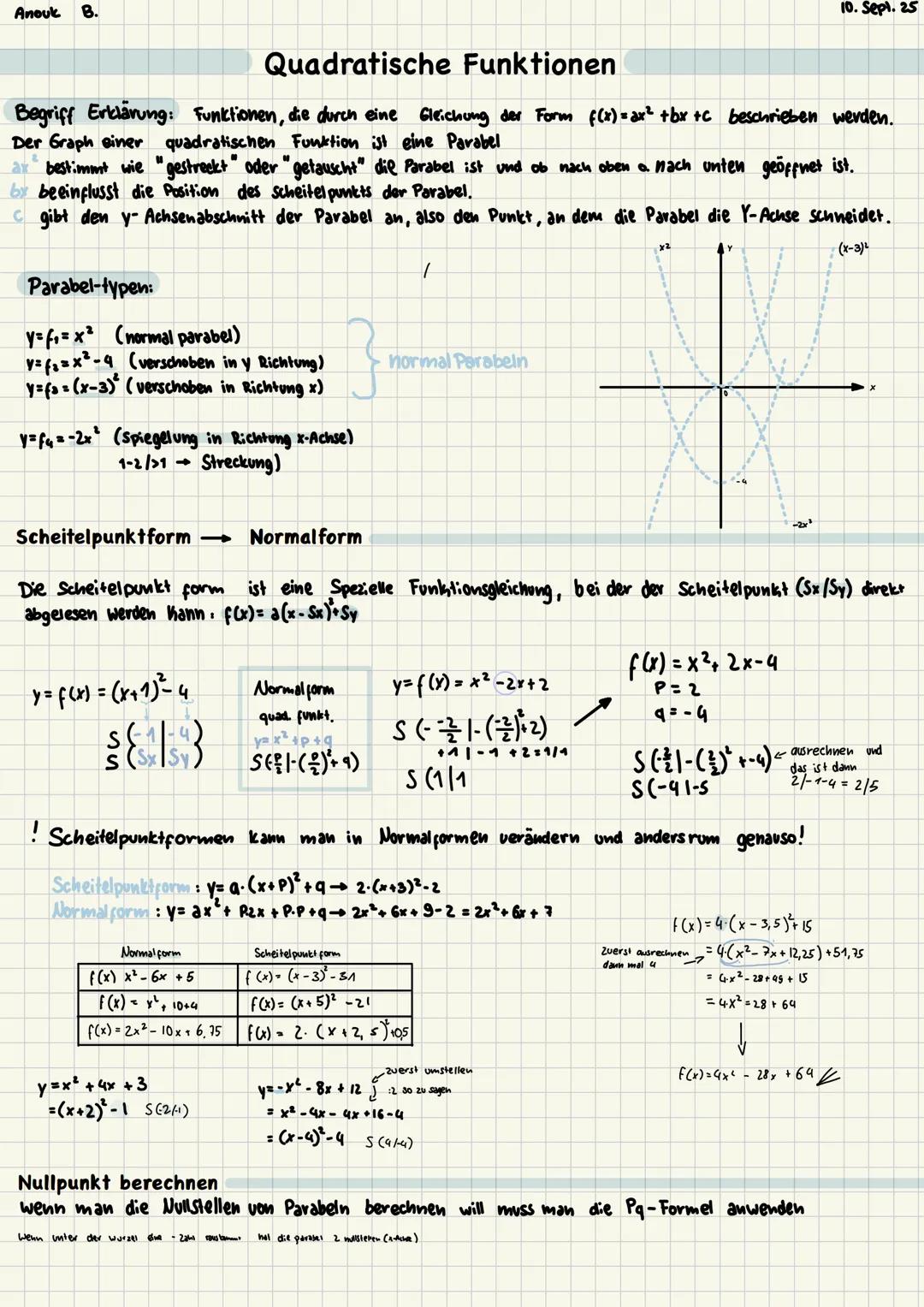
Quadratische Funktionen haben die Form f(x) = ax² + bx + c und ihr Graph ist immer eine Parabel. Das klingt kompliziert, aber ist eigentlich ganz logisch aufgebaut.
Der Parameter a entscheidet, ob die Parabel nach oben oder unten geöffnet ist und wie "breit" sie aussieht. Ist a positiv, öffnet sich die Parabel nach oben - ist a negativ, zeigt sie nach unten. Der Parameter b verschiebt den Scheitelpunkt seitlich, während c den y-Achsenabschnitt angibt.
Es gibt verschiedene Parabel-Typen: Die normale Parabel y = x², nach unten verschobene wie y = x² - 9, oder nach rechts verschobene wie y = x−3². Eine gespiegelte Parabel sieht so aus: y = -2x².
Merktipp: Der Parameter a ist wie ein "Direktor" - er bestimmt die Hauptrichtung und Form der Parabel!
Du kannst zwischen Scheitelpunktform f(x) = ax−h² + k und Normalform f(x) = ax² + bx + c hin und her umformen. In der Scheitelpunktform kannst du den Scheitelpunkt direkt ablesen: S(h|k). Bei der Normalform berechnest du ihn mit der Formel S−p/2∣(−p/2)2+q.