Grundlagen und die Normalparabel
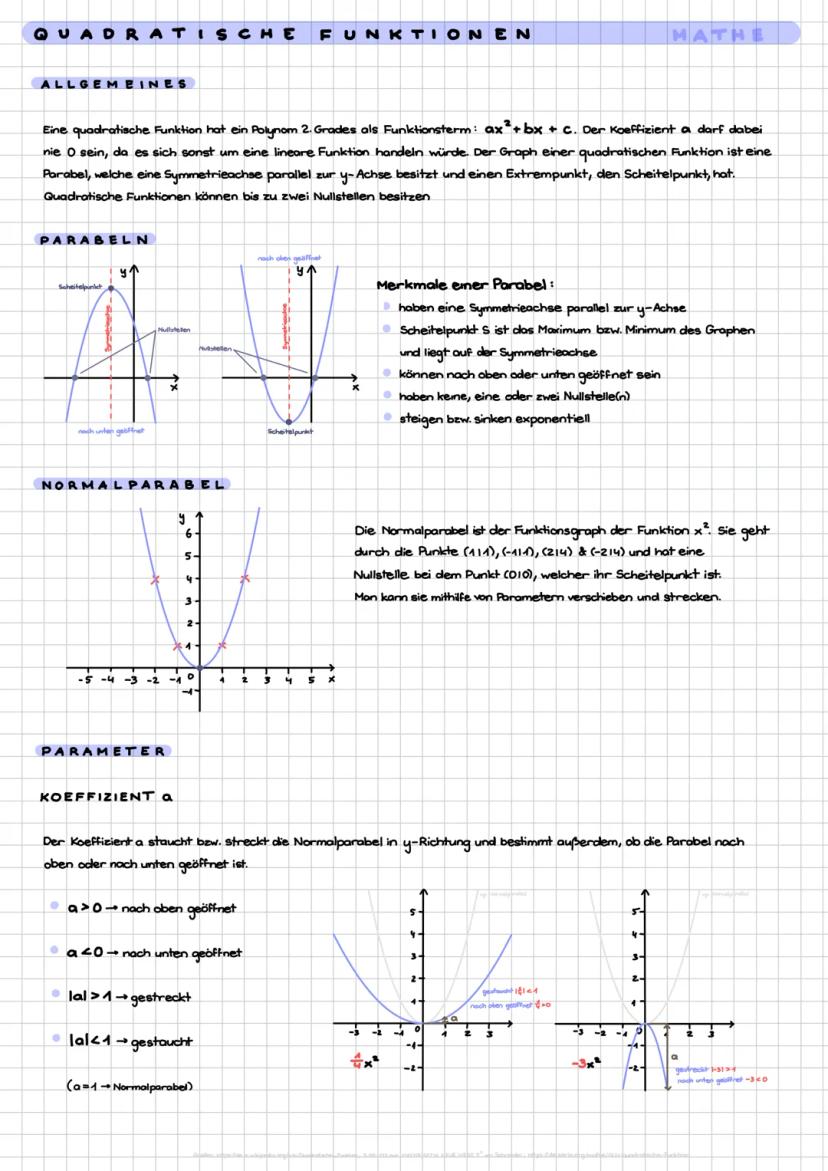
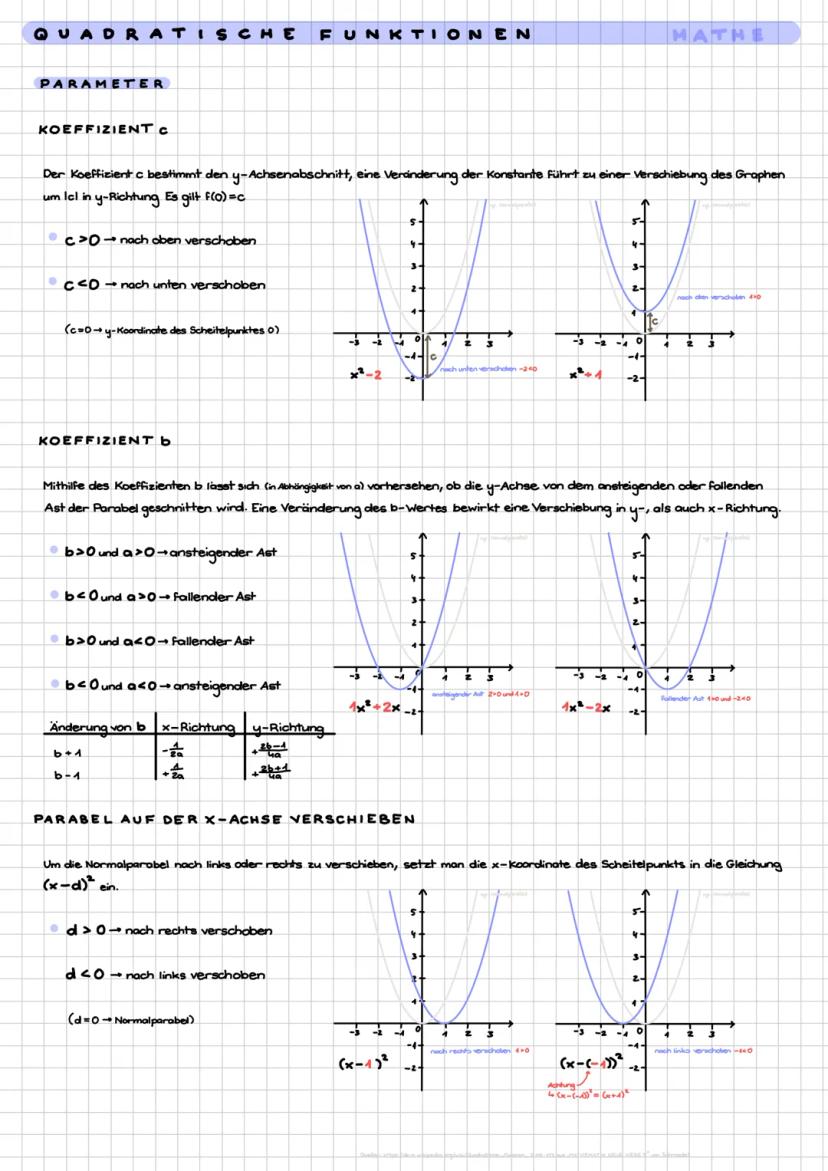
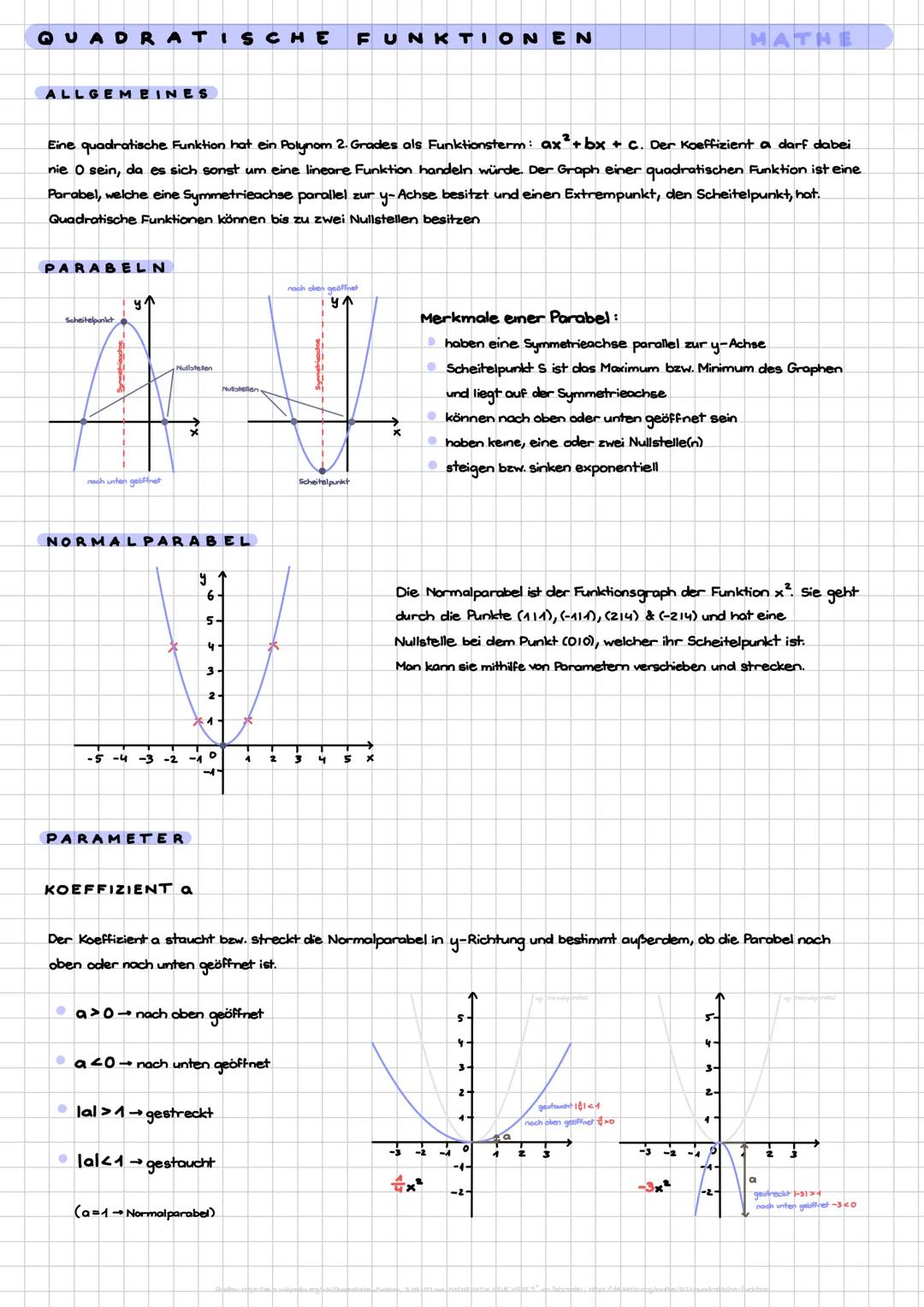
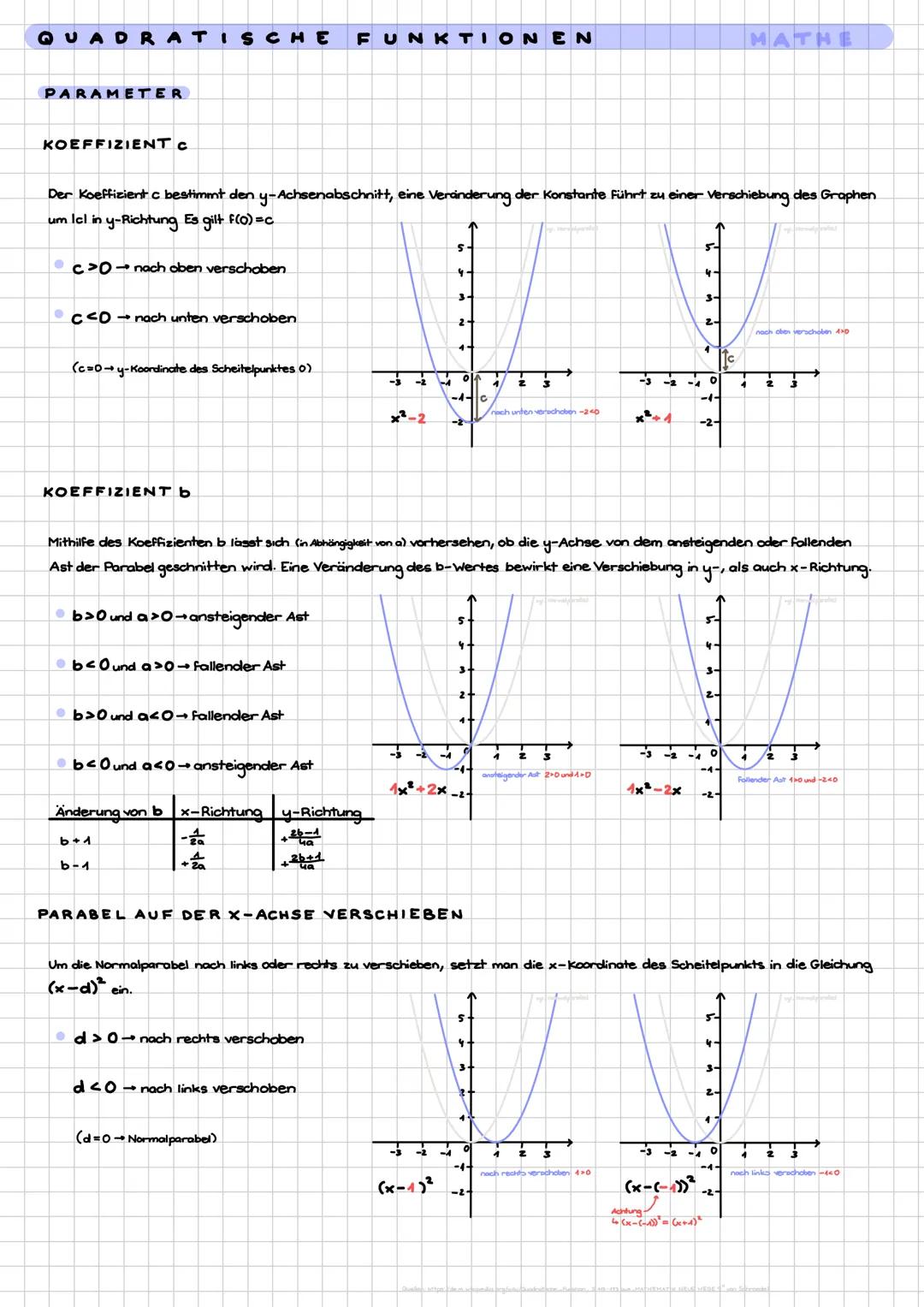
Stell dir vor, du wirfst einen Ball - die Kurve, die er beschreibt, ist eine Parabel! Eine quadratische Funktion hat immer die Form ax2+bx+c, wobei a niemals 0 sein darf (sonst wäre es ja keine Parabel mehr).
Die Normalparabel ist dein Ausgangspunkt - das ist einfach f(x)=x2. Sie geht durch die Punkte (1|1), (-1|1), (2|4) und (-2|4) und hat ihren tiefsten Punkt bei (0|0) - das ist der Scheitelpunkt.
Der Koeffizient a ist wie ein Zauberstab für deine Parabel. Ist a>0, öffnet sich die Parabel nach oben wie ein Lächeln. Ist a<0, öffnet sie sich nach unten wie ein trauriger Mund. Je größer ∣a∣ ist, desto schmaler wird die Parabel - je kleiner, desto breiter.
Merktipp: Jede Parabel hat eine Symmetrieachse parallel zur y-Achse und kann maximal zwei Nullstellen haben!