Sinus-Aufgaben lösen - Drei verschiedene Fälle
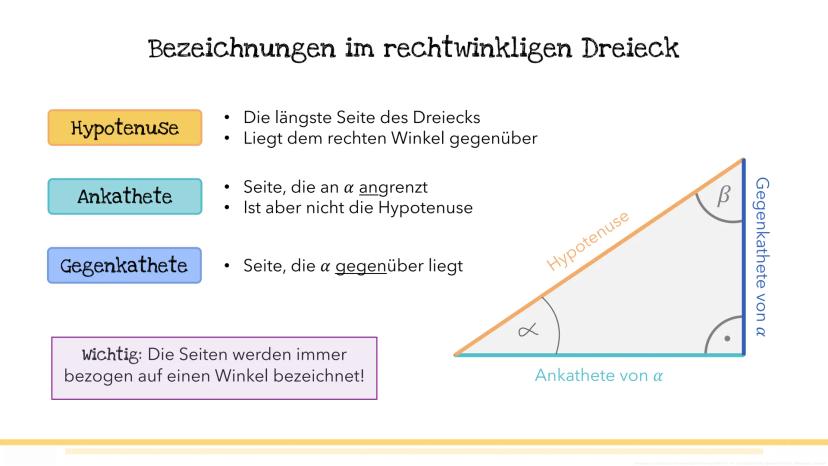
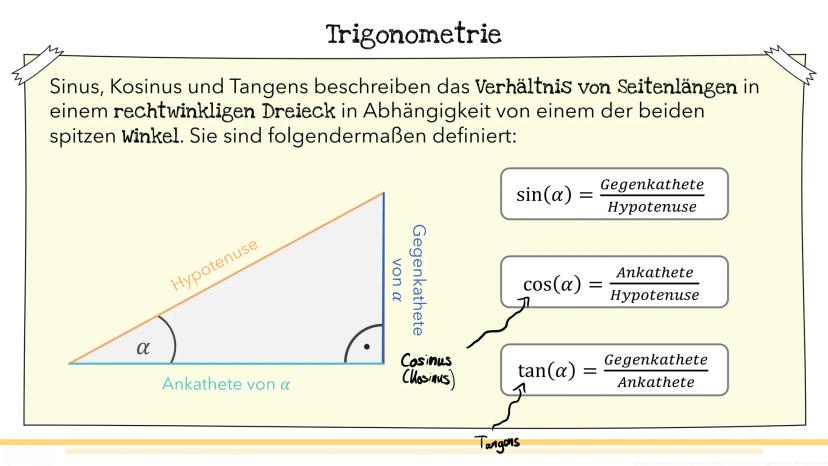
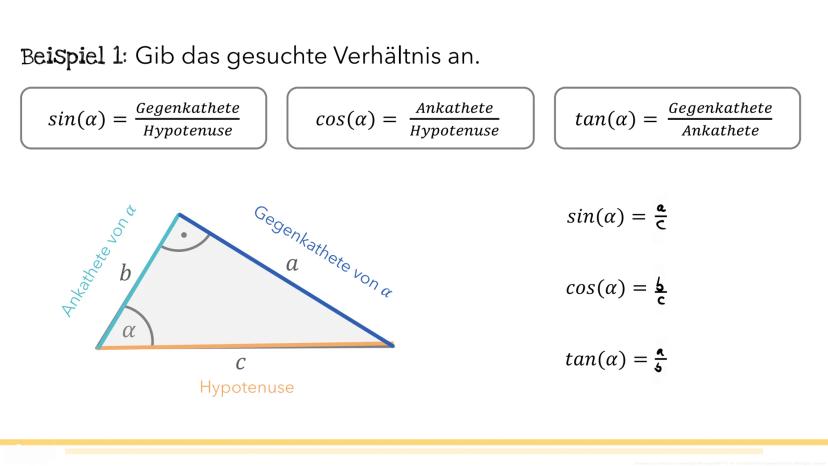
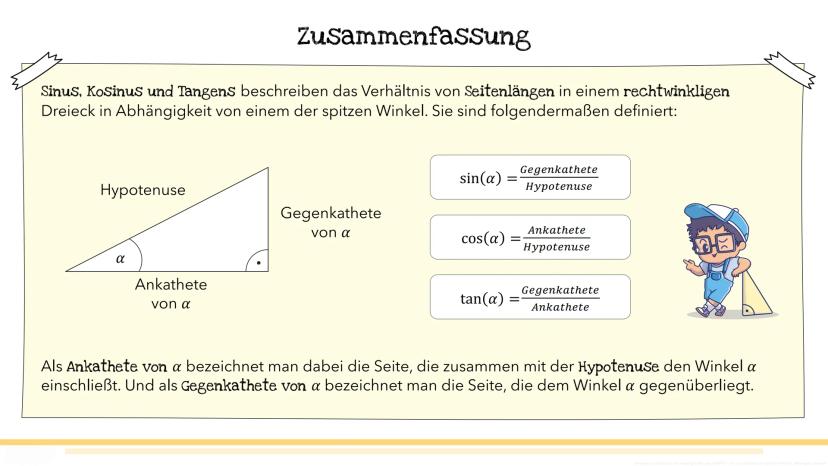
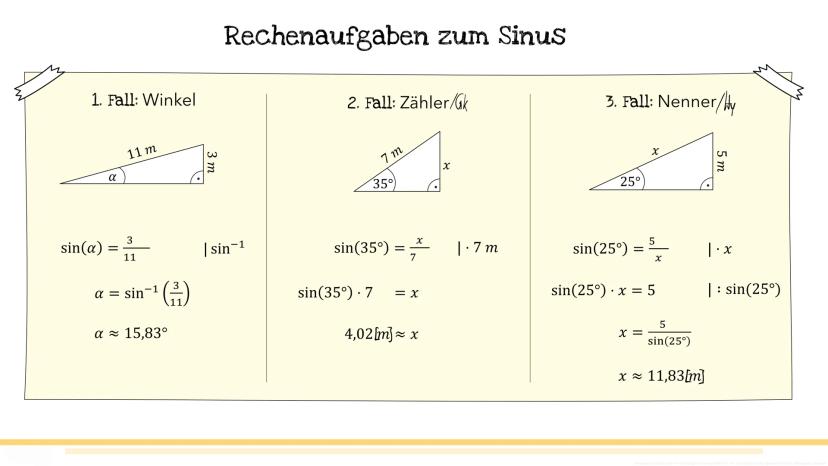
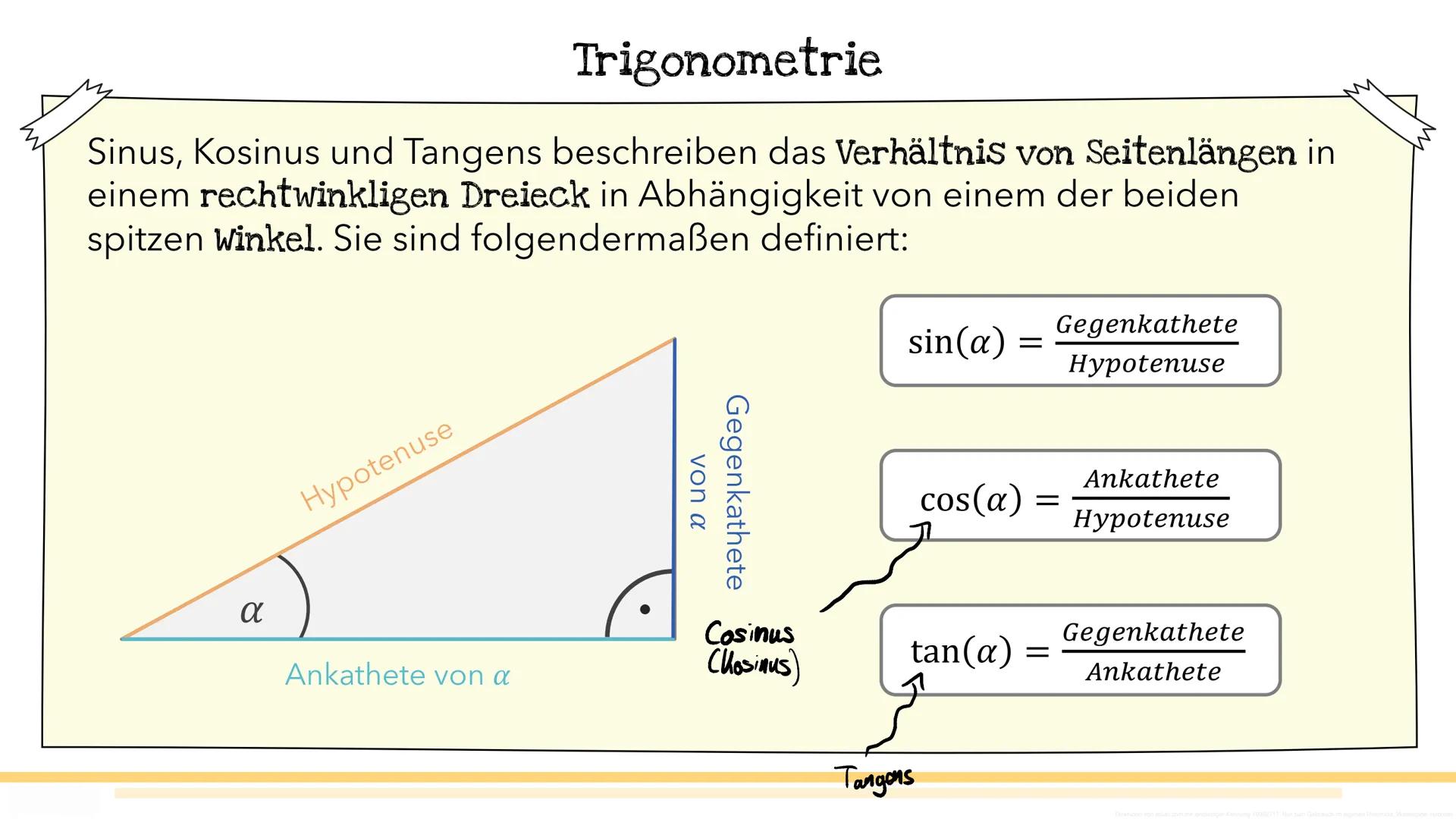
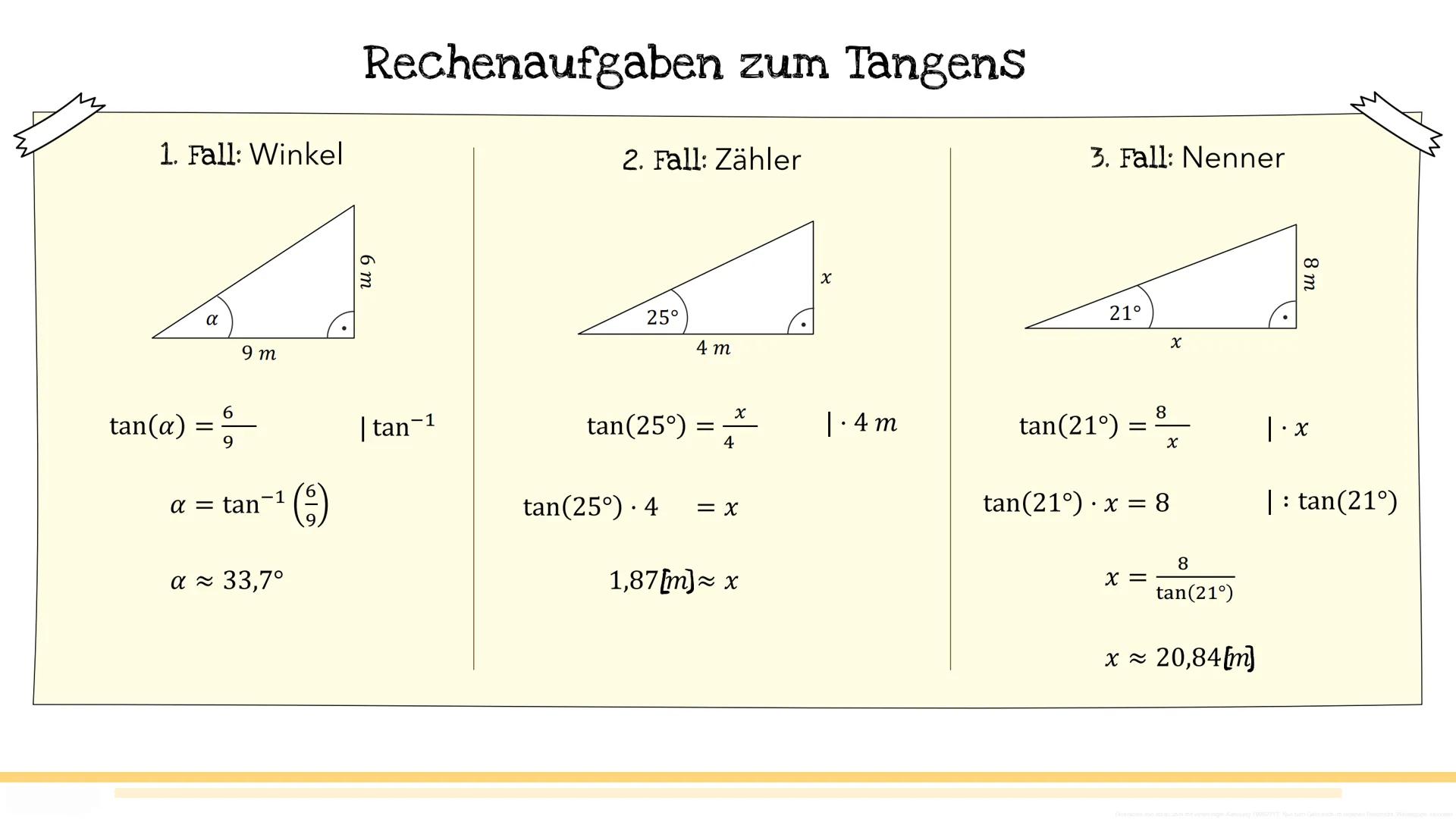
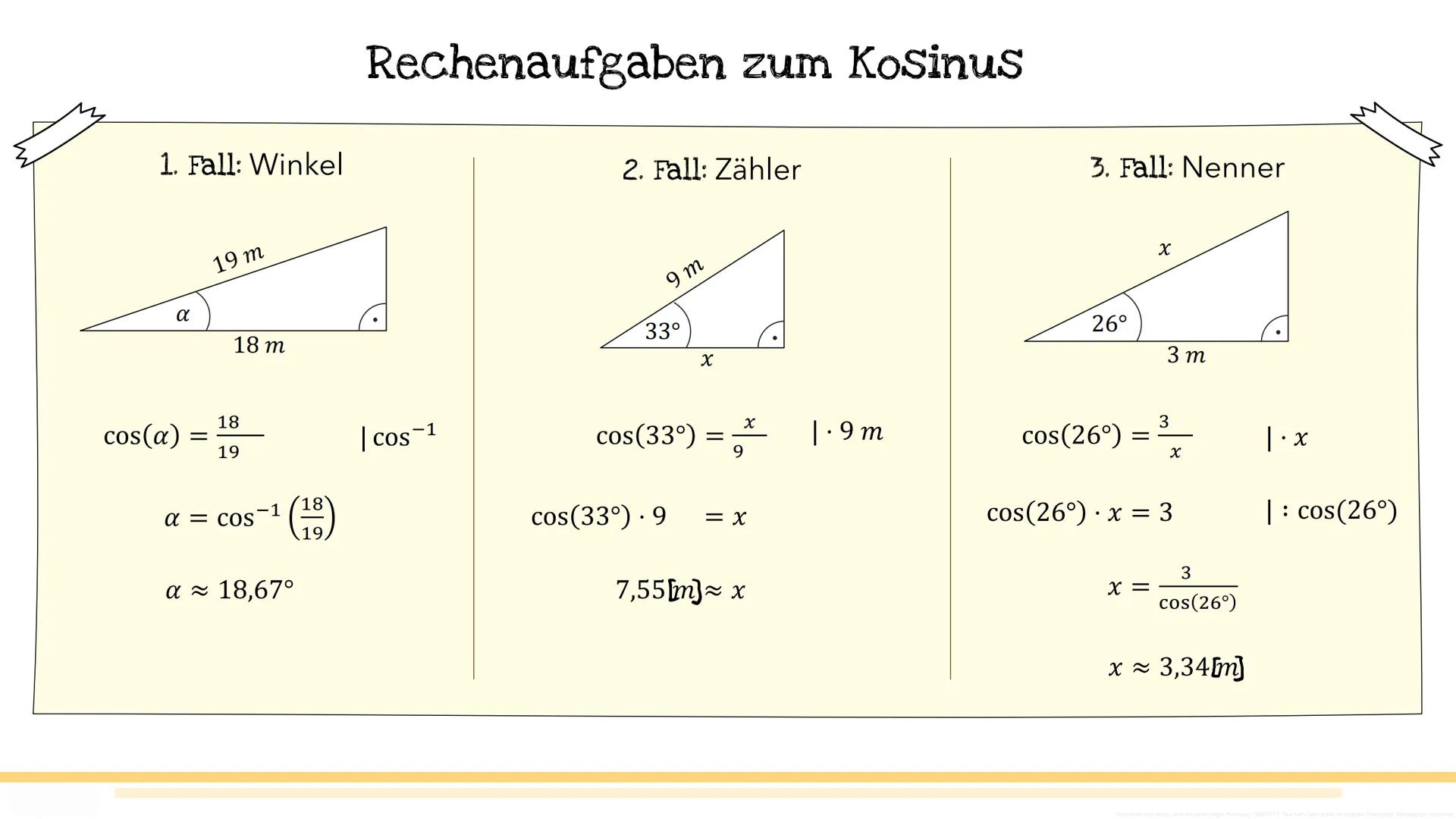
Zeit für echte Rechenaufgaben! Beim Sinus gibt es drei typische Situationen, die dir in Tests begegnen werden.
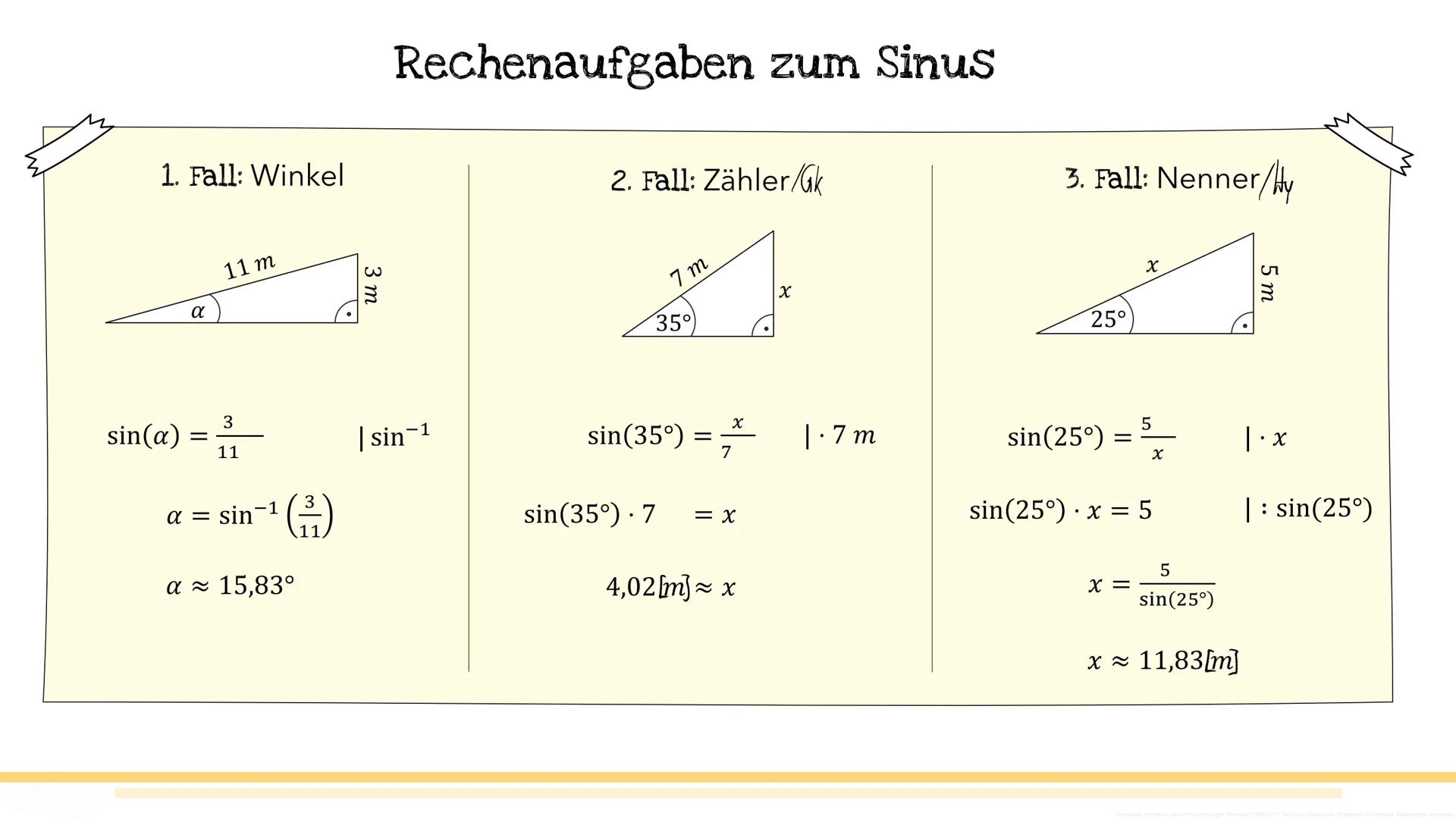
Fall 1 - Winkel gesucht: Du kennst beide Seiten und suchst den Winkel. Beispiel: sin(α)=113, dann ist α=sin−1(113)≈15,83°. Fall 2 - Gegenkathete gesucht: sin(35°)=7x, also x=sin(35°)⋅7≈4,02m. Fall 3 - Hypotenuse gesucht: sin(25°)=x5, also x=sin(25°)5≈11,83m.
Der Trick ist, die Gleichung nach der gesuchten Größe umzustellen. Das schaffst du!
Rechentipp: Vergiss nicht, deinen Taschenrechner auf "Grad" einzustellen, nicht auf "Rad"!