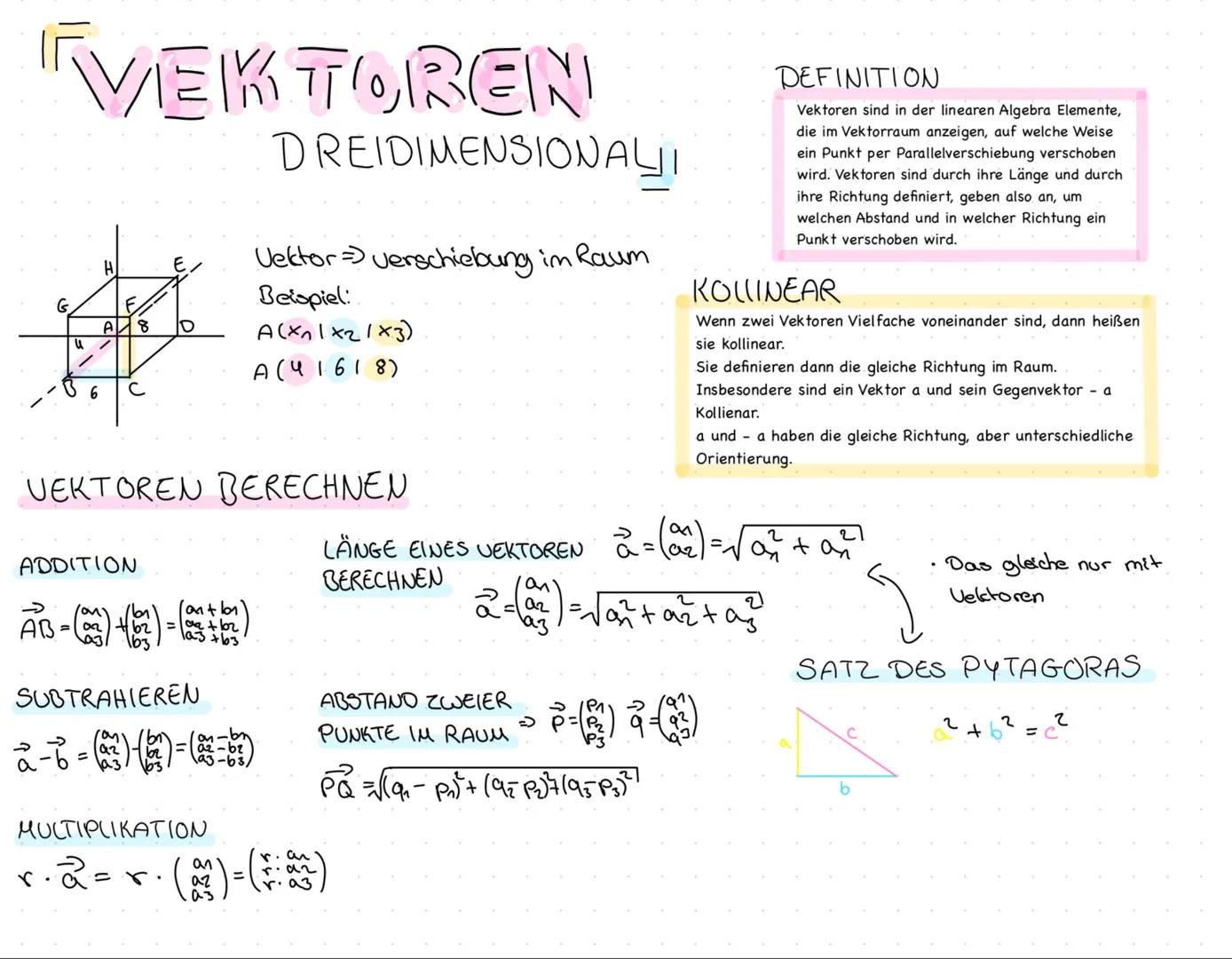
Dreidimensionale Vektoren - Grundlagen und Berechnungen
Vektoren sind mathematische Objekte, die eine Parallelverschiebung im Raum beschreiben. Stell dir vor, du willst jemandem erklären, wie er von einem Punkt A zu einem Punkt B kommt - genau das macht ein Vektor!
Ein Vektor wird durch seine Länge und Richtung definiert. Du kannst dir das wie einen Pfeil vorstellen, der dir sagt: "Gehe so weit in diese Richtung." Im dreidimensionalen Raum braucht ein Vektor drei Komponenten: x, y und z.
Vektoroperationen funktionieren ganz einfach:
- Addition: Du addierst einfach die entsprechenden Komponenten zusammen
- Subtraktion: Ziehe die Komponenten voneinander ab
- Multiplikation mit einer Zahl: Multipliziere jede Komponente mit dieser Zahl
Die Länge eines Vektors berechnest du mit dem Satz des Pythagoras - nur diesmal in drei Dimensionen! Die Formel ist: √a12+a22+a32.
Merktipp: Wenn zwei Vektoren kollinear sind, zeigen sie in dieselbe oder entgegengesetzte Richtung - wie zwei parallele Pfeile!