Übersicht der Abitur-Themen

Hier siehst du auf einen Blick, was in Mathe auf dich zukommt. Die drei Hauptbereiche Stochastik, Analysis und Analytische Geometrie bilden das Fundament deiner Abiturprüfung.

Bei der Stochastik geht's um Wahrscheinlichkeitsrechnung - von Baumdiagrammen über bedingte Wahrscheinlichkeiten bis hin zur Binomialverteilung. Das ist das Gebiet, wo du lernst, Zufälle mathematisch zu beschreiben.

Die Analysis dreht sich um Funktionen und ihre Eigenschaften. Du untersuchst Graphen, berechnest Flächen mit Integralen und modellierst Wachstumsprozesse.

In der Analytischen Geometrie arbeitest du mit Vektoren, Geraden und Ebenen im dreidimensionalen Raum. Hier wird Geometrie richtig rechnerisch.

Tipp: Diese Übersicht ist dein Masterplan - hake ab, was du schon kannst, und fokussiere dich auf deine Schwachstellen.

Stochastik Grundlagen

Baumdiagramme sind dein bester Freund bei mehrstufigen Zufallsexperimenten. Du multiplizierst die Wahrscheinlichkeiten entlang eines Pfades und addierst sie, wenn du mehrere Ergebnisse zu einem Ereignis zusammenfasst.

Zufallsgrößen ordnen jedem Ergebnis einen Zahlenwert zu. Der Erwartungswert μ zeigt dir, was bei unendlich vielen Versuchen im Durchschnitt rauskommen würde: μ = Σ$xi · P(X = xi)$. Bei der Binomialverteilung gilt einfach μ = n · p.

Die Varianz V(X) misst, wie stark die Werte um den Erwartungswert streuen: V(X) = Σ$xi - μ$² · P$X = xi$. Die Standardabweichung σ ist die Wurzel aus der Varianz und gibt dir ein Gefühl für die typische Abweichung.

Mit dem Taschenrechner wird's viel einfacher: mean() für den Erwartungswert, sum$(werte - x̄)² · wahrscheinlichkeit$ für die Varianz.

Merksatz: Ein faires Spiel liegt vor, wenn der Erwartungswert gleich null ist - niemand hat einen systematischen Vorteil.

Bedingte Wahrscheinlichkeiten und Vierfeldertafeln

Vierfeldertafeln sind genial, wenn du zwei Merkmale mit jeweils zwei Ausprägungen hast. Sie helfen dir, komplexe Wahrscheinlichkeitsprobleme übersichtlich zu strukturieren.

In der Tafel trägst du entweder absolute oder relative Häufigkeiten ein. Die Randsummen geben dir die Wahrscheinlichkeiten für die einzelnen Merkmale.

Bedingte Wahrscheinlichkeiten berechnest du mit P_A(B) = P(A∩B)/P(A). Das ist die Wahrscheinlichkeit für B, wenn du bereits weißt, dass A eingetreten ist.

Beim Baumdiagramm gehst du in zwei Stufen vor: Erst das erste Merkmal, dann das zweite mit den bedingten Wahrscheinlichkeiten. Die Pfadwahrscheinlichkeiten multiplizierst du wie gewohnt.

Praxis-Tipp: Vierfeldertafeln sind besonders nützlich bei Aufgaben mit Krankheitstests oder Qualitätskontrollen.

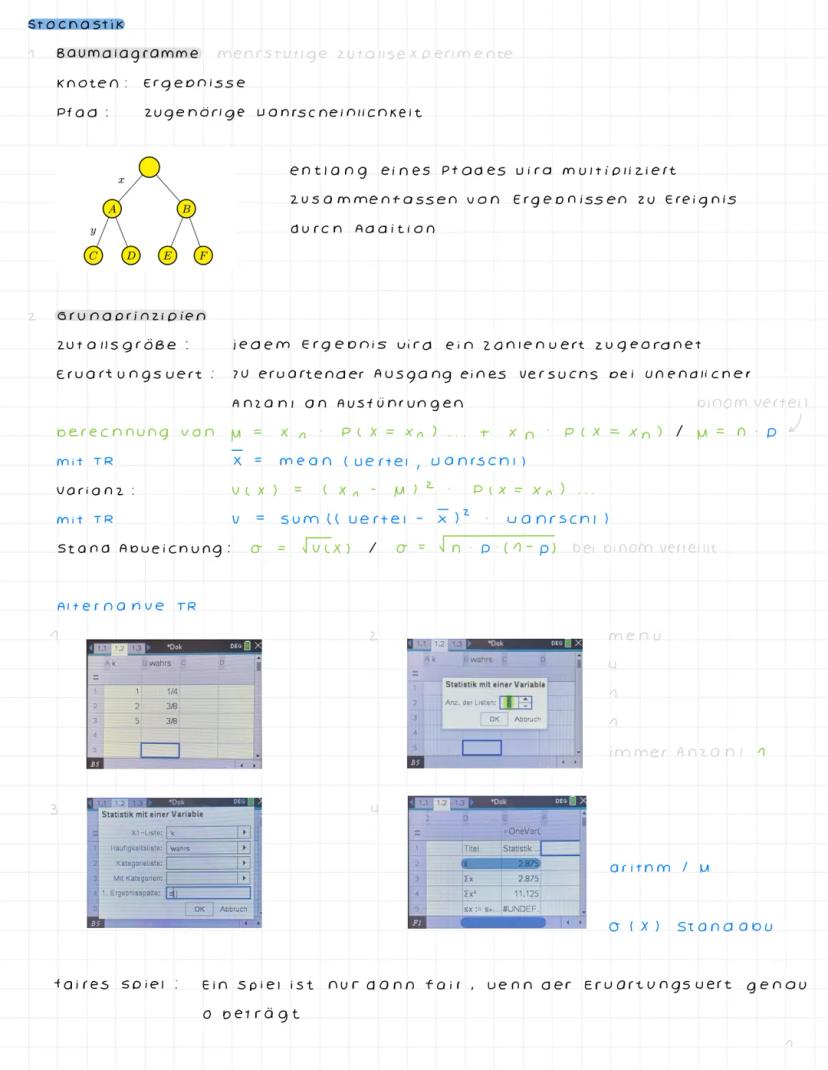
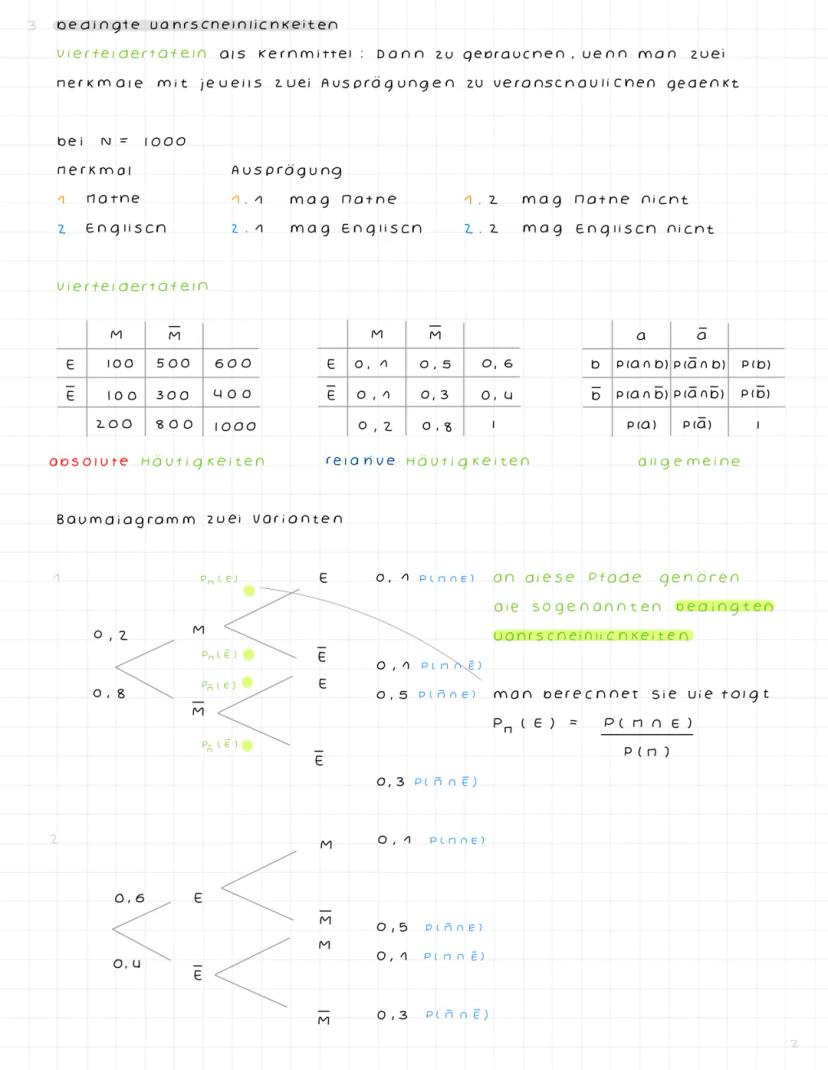
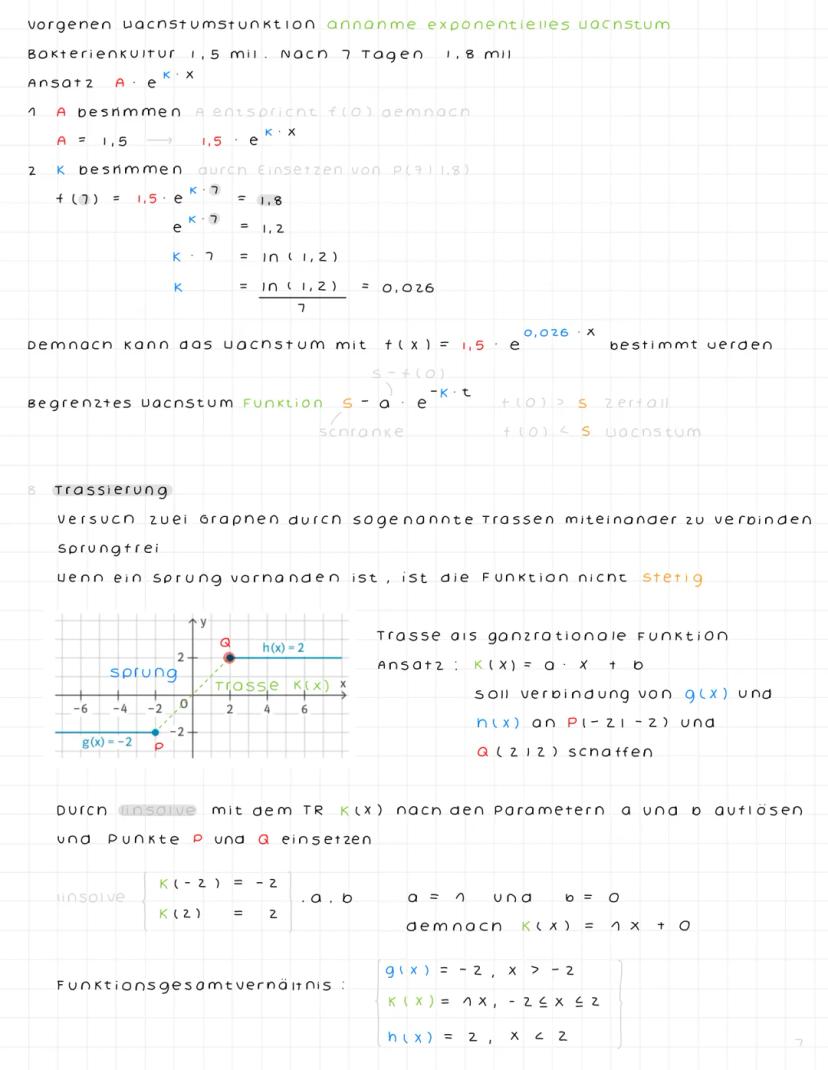
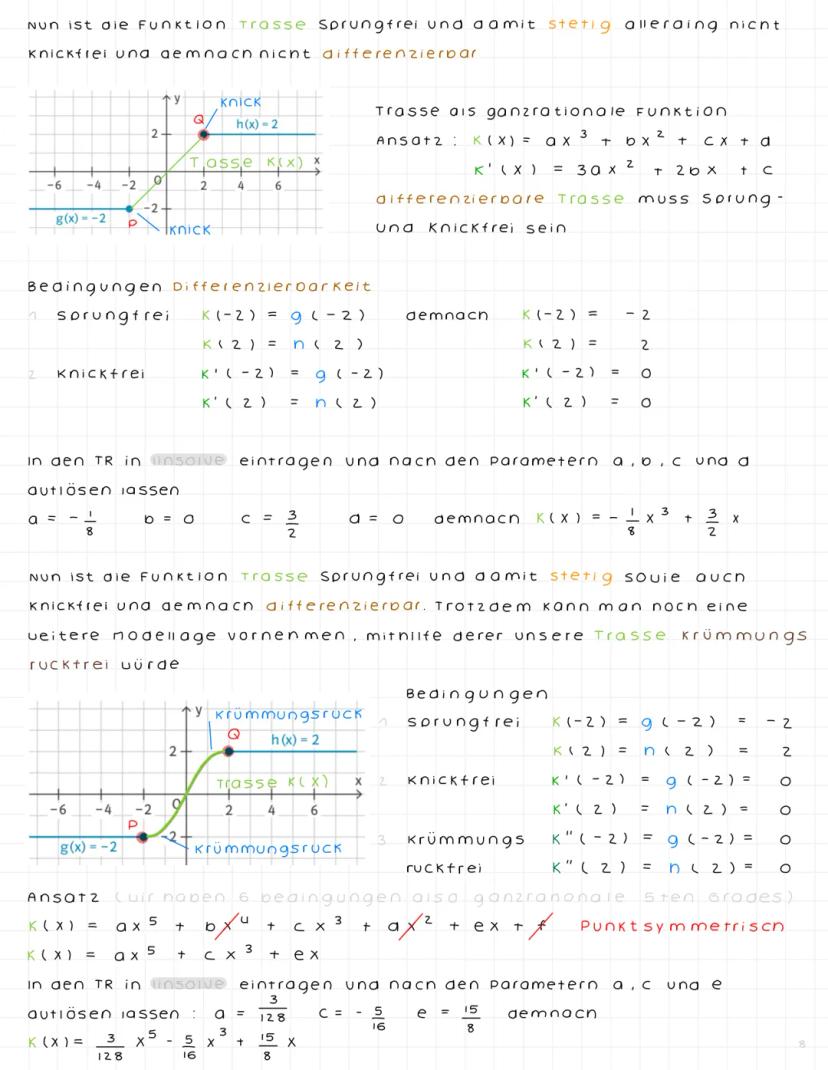
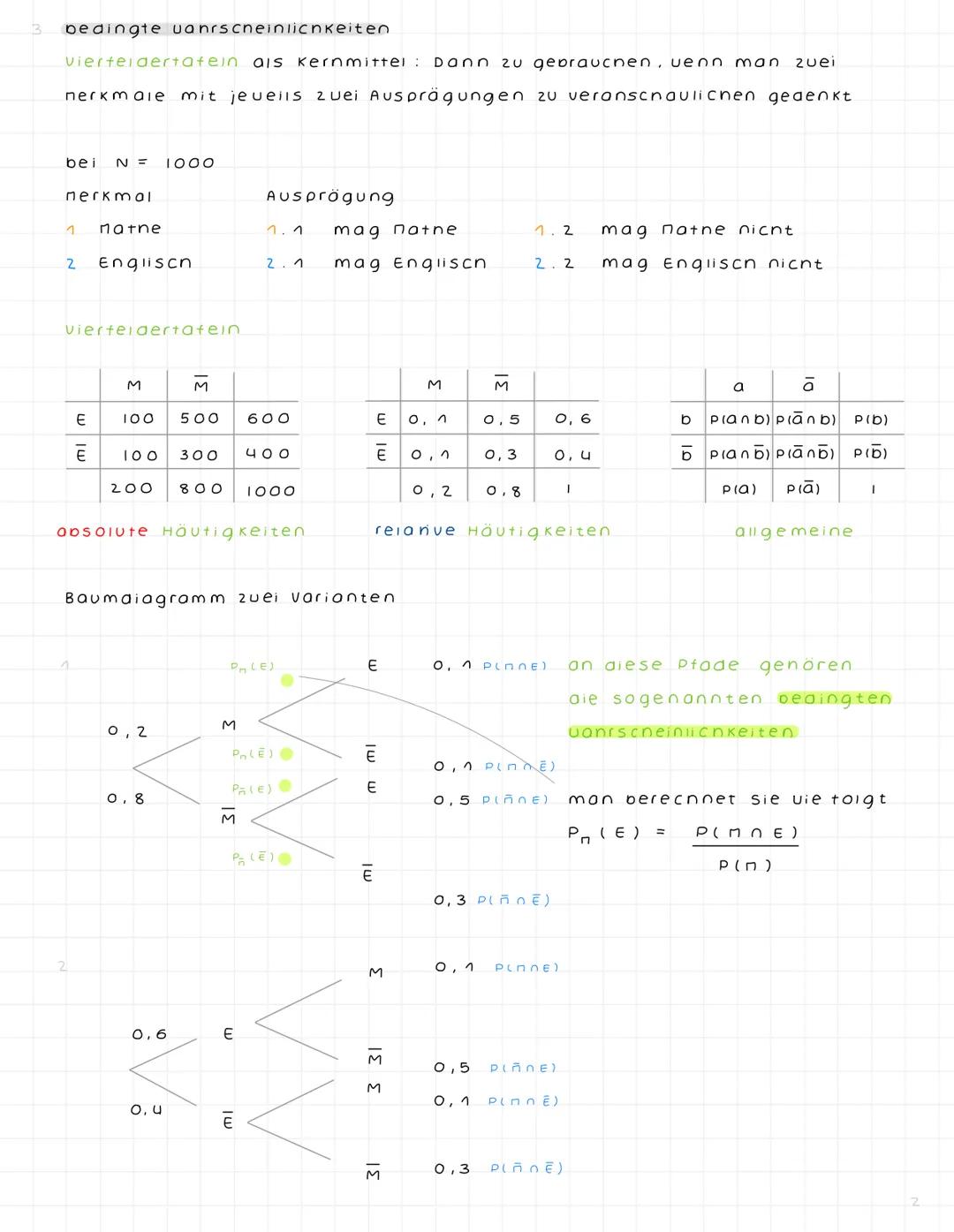
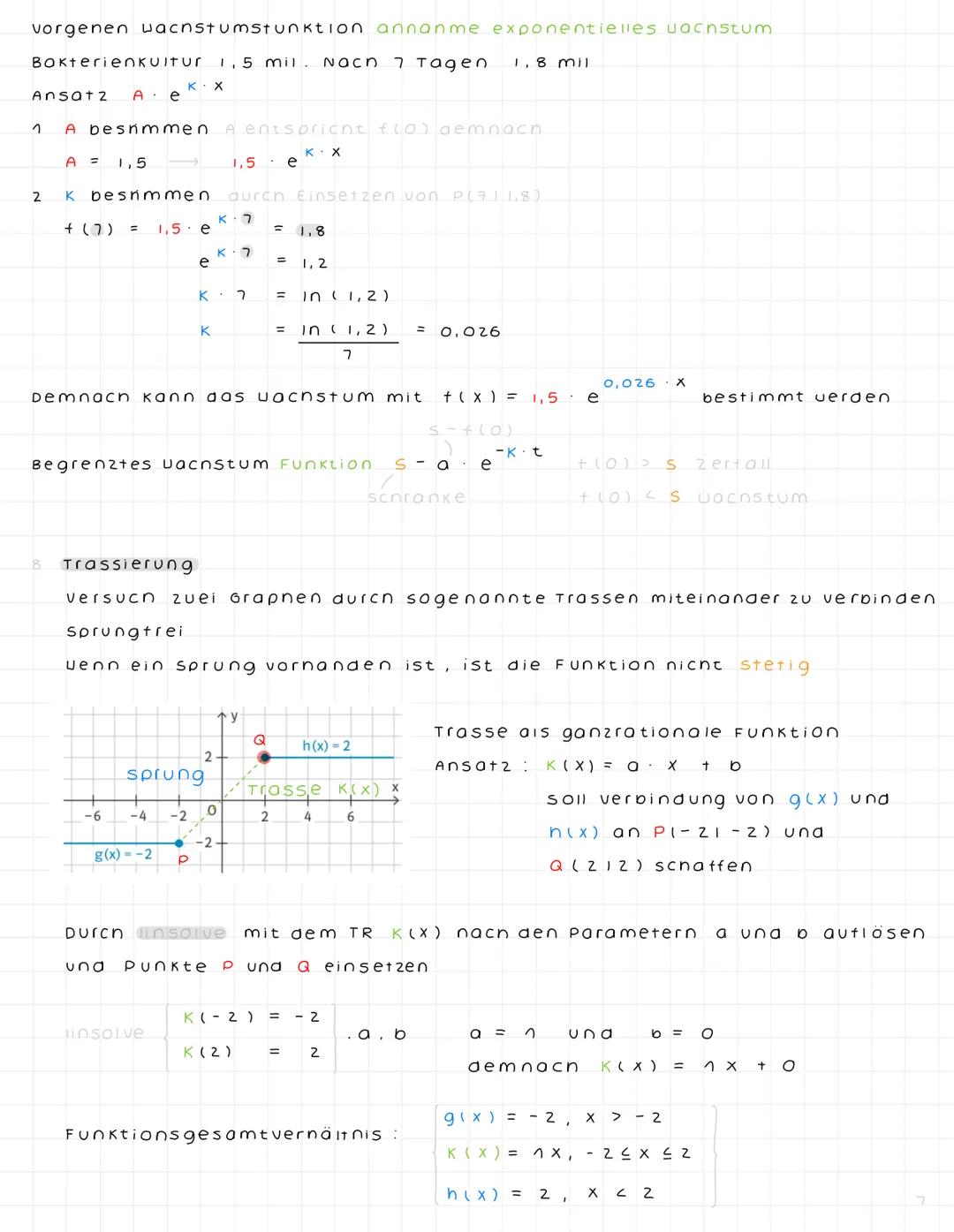
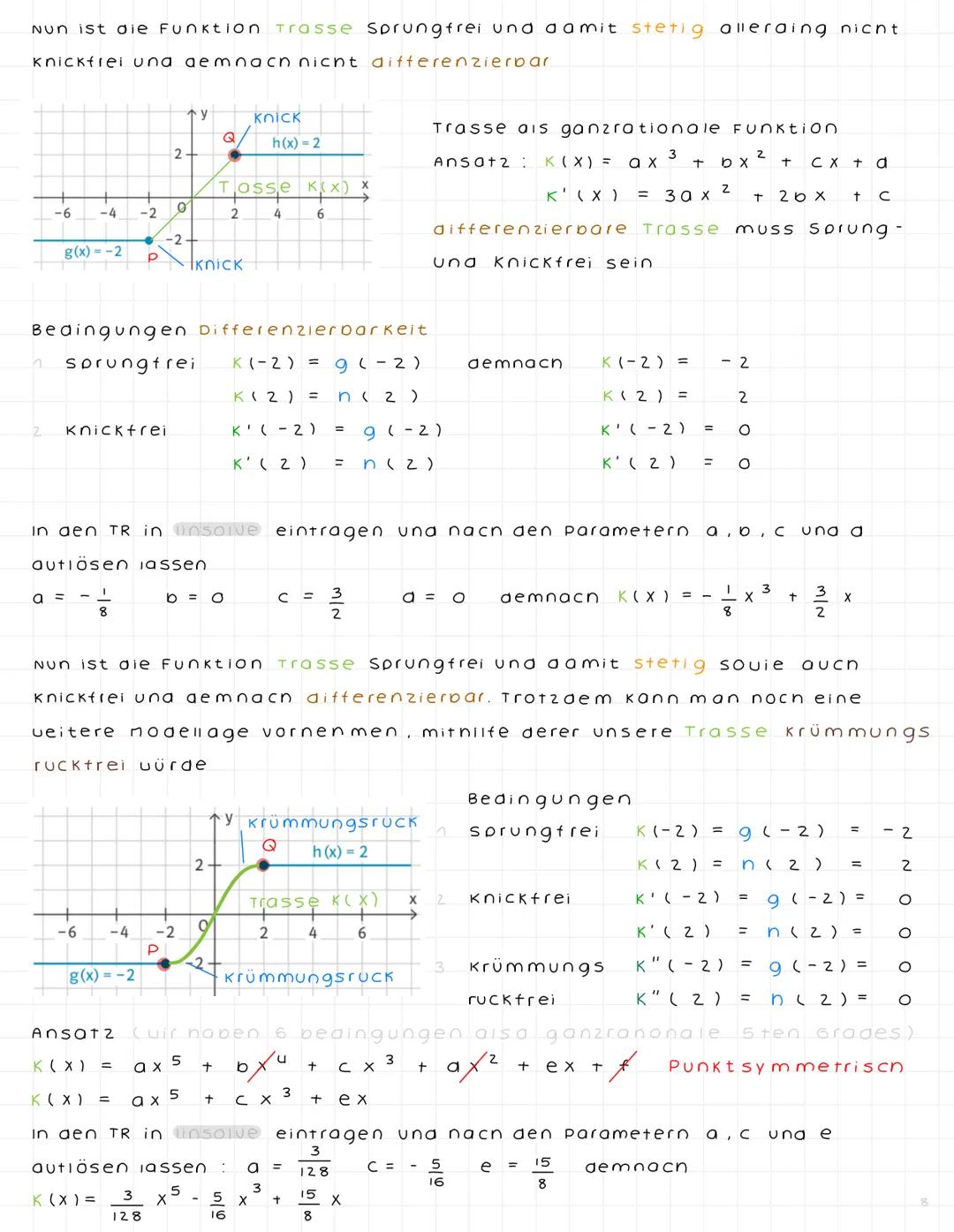
Stochastische Unabhängigkeit und Binomialverteilung

Zwei Ereignisse A und B sind stochastisch unabhängig, wenn P(A) = P_B(A) gilt. Alternativ kannst du prüfen: P(A) · P(B) = P(A∩B). Das bedeutet, dass das eine Ereignis das andere nicht beeinflusst.

Die Binomialverteilung verwendest du bei n-maligen Wiederholungen eines Bernoulli-Experiments mit konstanter Erfolgswahrscheinlichkeit p. Die Bernoulli-Formel lautet: P$X=k$ = (n über k) · p^k · $1-p$^$n-k$.

Mit dem Taschenrechner wird's einfach: binompdf(n,p,k) für Einzelwahrscheinlichkeiten, nCr(n,k) für Binomialkoeffizienten.

Kumulierte Wahrscheinlichkeiten berechnest du mit binomcdf(). Achte auf die verschiedenen Varianten: P(X ≤ k), P(X ≥ k) = 1 - P$X ≤ k-1$, oder P(j ≤ X ≤ k).

Die Verteilung ist symmetrisch bei p = 0,5, bei p > 0,5 nach rechts verschoben, bei p < 0,5 nach links.

Abitur-Trick: Bei "mindestens"-Aufgaben oft über das Gegenereignis gehen - das spart Rechenzeit.

Binomialverteilung - Problemtypen

Du wirst drei Haupttypen von Aufgaben begegnen, die jeweils verschiedene Lösungsstrategien erfordern.

Problem 1 - Wahrscheinlichkeit gesucht: Du hast n, p und k gegeben und suchst P(X ≤ k) oder ähnliches. Einfach binomcdf() verwenden.

Problem 2 - Anzahl k gesucht: Du hast n, p und eine Mindestwahrscheinlichkeit gegeben. Verwende invbinom() oder probiere systematisch Werte aus, bis die Bedingung erfüllt ist.

Problem 3 - Gesamtzahl n gesucht: Hier musst du oft ausprobieren oder das Gegenereignis modellieren. Bei P(X ≥ k) ≥ 0,9 rechnest du mit P$X ≤ k-1$ ≤ 0,1 und verwendest invbinom.

Problem 4 - Erfolgswahrscheinlichkeit p gesucht: Entweder systematisches Ausprobieren mit binomcdf oder die solve-Funktion des Taschenrechners nutzen.

Strategie-Tipp: Bei unbekanntem n oder p immer erst überlegen, ob das Gegenereignis einfacher zu handhaben ist.

Analysis - Funktionsuntersuchung

Nullstellen findest du durch Lösen von f(x) = 0. Der Taschenrechner hilft mit zeros(f(x),x).

Für Extrema brauchst du die notwendige Bedingung f'(x) = 0 und die hinreichende f''(x) ≠ 0. Ist f''(x) > 0, hast du ein Minimum, ist f''(x) < 0, ein Maximum.

Wendepunkte ergeben sich aus f''(x) = 0 (notwendig) und f'''(x) ≠ 0 (hinreichend). Ist f'''(x) > 0, wechselt die Krümmung von Rechts- zu Linkskrümmung, bei f'''(x) < 0 umgekehrt.

Symmetrie erkennst du so: Achsensymmetrie liegt vor, wenn alle Exponenten gerade sind und f$-x$ = f(x) gilt. Punktsymmetrie zum Ursprung bei ungeraden Exponenten und f$-x$ = -f(x).

Das Verhalten für große x-Beträge bestimmt bei Polynomen der höchste Term. Bei geradem Grad gehen beide Äste in dieselbe Richtung, bei ungeradem Grad in entgegengesetzte.

Klausur-Tipp: Führe immer eine vollständige Funktionsuntersuchung durch - das gibt die meisten Punkte.

Stammfunktionen und Integration

Stammfunktionen bildest du mit der Grundregel: ax^n wird zu $a/(n+1)$x^$n+1$. Das ist die Umkehrung des Ableitens.

Wichtige Spezialfälle: √x wird zu (2/3)x^(3/2), 1/(ax) wird zu $1/a$ln(x), und bei zusammengesetzten Funktionen g$ax+b$ teilst du durch den inneren Faktor a.

Bei Sinus und Kosinus läuft der Ableitungskreis rückwärts: cos wird zu sin, sin wird zu -cos.

Bestimmte Integrale berechnest du mit dem Hauptsatz: ∫$a bis b$ f(x)dx = F(b) - F(a). Das gibt dir die orientierte Fläche zwischen Graph und x-Achse.

Für Flächeninhalte zwischen zwei Graphen bildest du ∫$a bis b$ |f(x) - g(x)|dx. Vorher die Schnittpunkte bestimmen!

Wachstumsmodelle haben die Form A·e^(kt). Hier ist A der Anfangswert, k > 0 bedeutet Wachstum, k < 0 Zerfall.

Integration-Hack: Bei komplizierten Termen immer erst schauen, ob eine lineare Substitution möglich ist.

Exponentielles Wachstum und Kurvendiskussion

Bei Wachstumsproblemen stellst du den Ansatz f(t) = A·e^(kt) auf. Den Anfangswert A bekommst du aus f(0) = A. Die Wachstumskonstante k bestimmst du durch Einsetzen eines weiteren Punktes.

Beispiel: 1,5 Mio. Bakterien wachsen in 7 Tagen auf 1,8 Mio. Dann ist A = 1,5 und aus 1,8 = 1,5·e^(7k) folgt k = ln(1,2)/7 ≈ 0,026.

Begrenztes Wachstum hat die Form S - a·e^$-kt$, wo S die Sättigungsgrenze ist.

Bei der Trassierung verbindest du verschiedene Funktionsabschnitte glatt miteinander. Eine stetige Trasse ist sprungfrei, eine differenzierbare zusätzlich knickfrei.

Für Differenzierbarkeit brauchst du: K(x₁) = f(x₁), K(x₂) = g(x₂) (Stetigkeit) und K'(x₁) = f'(x₁), K'(x₂) = g'(x₂) (keine Knicke).

Anwendungs-Tipp: Exponentielles Wachstum findest du überall - von Bakterien über Zinsen bis zu radioaktivem Zerfall.

Erweiterte Trassierung und Substitution

Für eine krümmungsruckfreie Trasse brauchst du zusätzlich die Bedingungen K''(x₁) = f''(x₁) und K''(x₂) = g''(x₂). Das führt zu Polynomen höheren Grades.

Mit 6 Bedingungen benötigst du einen Ansatz 5. Grades: K(x) = ax⁵ + bx⁴ + cx³ + dx² + ex + f. Bei Punktsymmetrie fallen die geraden Potenzen weg.

Die lineare Substitution hilft bei Integralen der Form ∫f$mx+b$ⁿ dx. Die Stammfunktion ist dann $1/(m(n+1))$$mx+b$^$n+1$.

Diese Technik funktioniert immer, wenn du eine "äußere" Funktion und eine "innere" lineare Funktion hast.

Effizienz-Tipp: Der Taschenrechner löst komplexe Gleichungssysteme für Trassierungsparameter automatisch - nutze linsolve().

Analytische Geometrie - Vektorgrundlagen

Vektoren beschreiben Verschiebungen im Raum. Du addierst sie komponentenweise, multiplizierst sie mit Zahlen (Skalare) und berechnest ihren Betrag mit |a⃗| = √$a₁² + a₂² + a₃²$.

Das Skalarprodukt a⃗·b⃗ = a₁b₁ + a₂b₂ + a₃b₃ ist eine Zahl. Ist es null, stehen die Vektoren senkrecht aufeinander (orthogonal).

Das Vektorprodukt a⃗ × b⃗ liefert einen Vektor, der senkrecht zu beiden ursprünglichen steht. Die Formel ist etwas kompliziert, aber der Taschenrechner macht das mit crossp().

Den Winkel zwischen Vektoren berechnest du über cos(α) = (a⃗·b⃗)/(|a⃗|·|b⃗|). Mit dem TR: dotP(a⃗,b⃗)/(norm(a⃗)·norm(b⃗)), dann arccos().

Diese Grundlagen brauchst du für alle weiteren Themen der analytischen Geometrie - Geraden, Ebenen, Abstände und Lagebeziehungen.

Vektor-Weisheit: Orthogonale Vektoren haben Skalarprodukt null - das ist der wichtigste Test für Senkrecht-Beziehungen.