Potenz- und ganzrationale Funktionen

Potenzfunktionen haben die Form f(x) = x^n und verhalten sich je nach Exponenten unterschiedlich. Bei geraden Exponenten ist der Graph achsensymmetrisch, bei ungeraden punktsymmetrisch zur y-Achse.

Ganzrationale Funktionen entstehen, wenn du Potenzfunktionen addierst oder subtrahierst: f(x) = a_n·x^n + ... + a_1·x + a_0. Der höchste Exponent bestimmt den Grad der Funktion - das ist super wichtig für das Verhalten der Funktion!

Nullstellen findest du, indem du f(x) = 0 setzt. Je nach Vielfachheit verhalten sie sich anders: einfache Nullstellen durchstoßen die x-Achse, doppelte berühren sie nur. Nutze Ausklammern, die p-q-Formel oder Substitution - je nachdem, was am besten passt.

Merktipp: Bei der Substitution ersetzt du x² durch z, um komplizierte Gleichungen zu vereinfachen!

Funktionseigenschaften verstehen

Das Globalverhalten einer ganzrationalen Funktion hängt nur vom höchsten Term ab. Bei geradem Grad geht die Funktion nach +∞ oder -∞, bei ungeradem Grad in entgegengesetzte Richtungen.

Monotonie beschreibt, ob eine Funktion steigt oder fällt. Streng monoton steigend bedeutet: größere x-Werte führen immer zu größeren y-Werten. Das erkennst du grafisch an der Steigung!

Symmetrie erkennst du am Funktionsterm: Nur gerade Exponenten = achsensymmetrisch zur y-Achse, nur ungerade Exponenten = punktsymmetrisch zum Ursprung. Extrema sind die höchsten und tiefsten Punkte - entweder lokal (in der Umgebung) oder global (im gesamten Graph).

Praxistipp: Checke bei Hausaufgaben immer zuerst die Symmetrie - das spart dir oft die Hälfte der Rechenarbeit!

Transformationen und Änderungsraten

Transformationen verschieben, strecken oder spiegeln Funktionsgraphen. Bei g(x) = f(x) + d verschiebst du um d nach oben/unten, bei g(x) = f$x-c$ um c nach rechts/links. Streckungen funktionieren mit Faktoren: |a| > 1 streckt, 0 < |a| < 1 staucht.

Änderungsraten messen, wie schnell sich etwas verändert. Die mittlere Änderungsrate ist die durchschnittliche Steigung zwischen zwei Punkten - rechne mit dem Differenzenquotienten $f(b)-f(a)$/$b-a$.

Die lokale Änderungsrate ist die momentane Steigung in einem Punkt. Du berechnest sie mit dem Differenzialquotienten: dem Grenzwert von $f(x+h)-f(x)$/h für h→0. Das ist die Grundlage für Ableitungen!

Aha-Moment: Die Ableitung gibt dir in jedem Punkt die exakte Steigung - wie das Tacho im Auto die momentane Geschwindigkeit anzeigt!

Ableitungen beherrschen

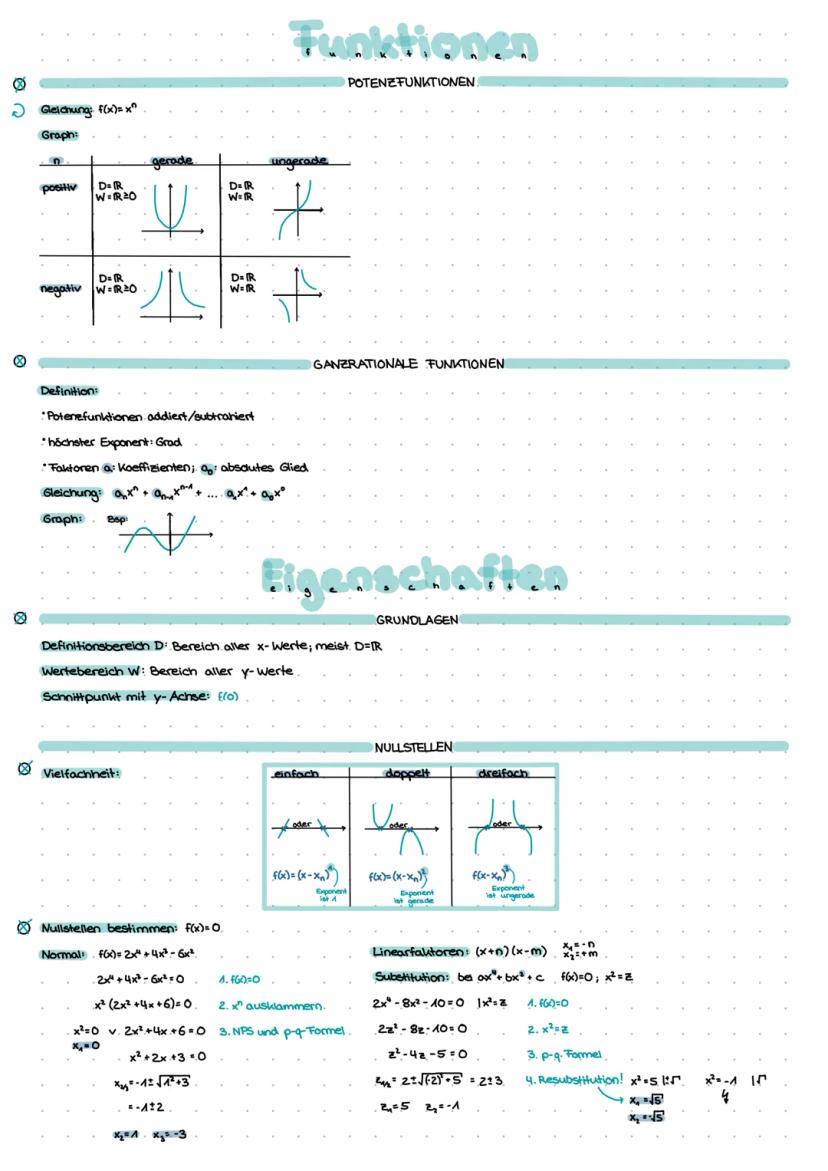
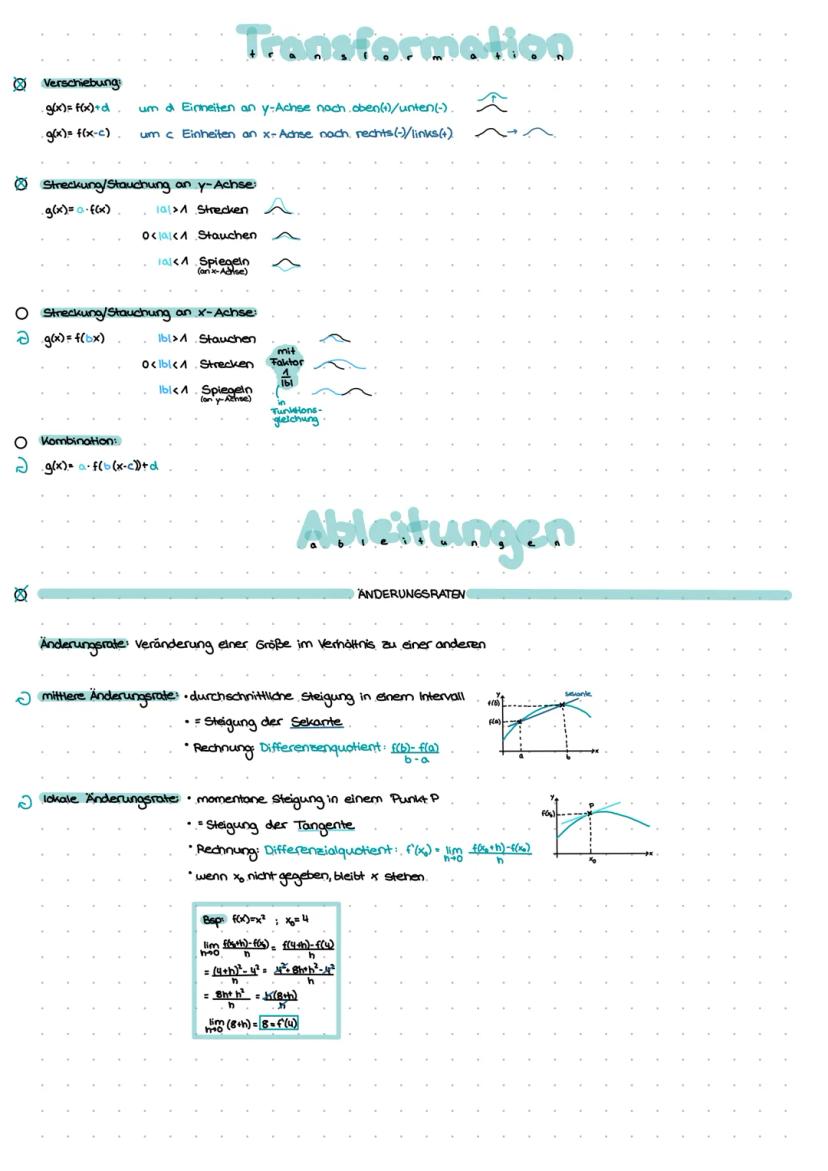
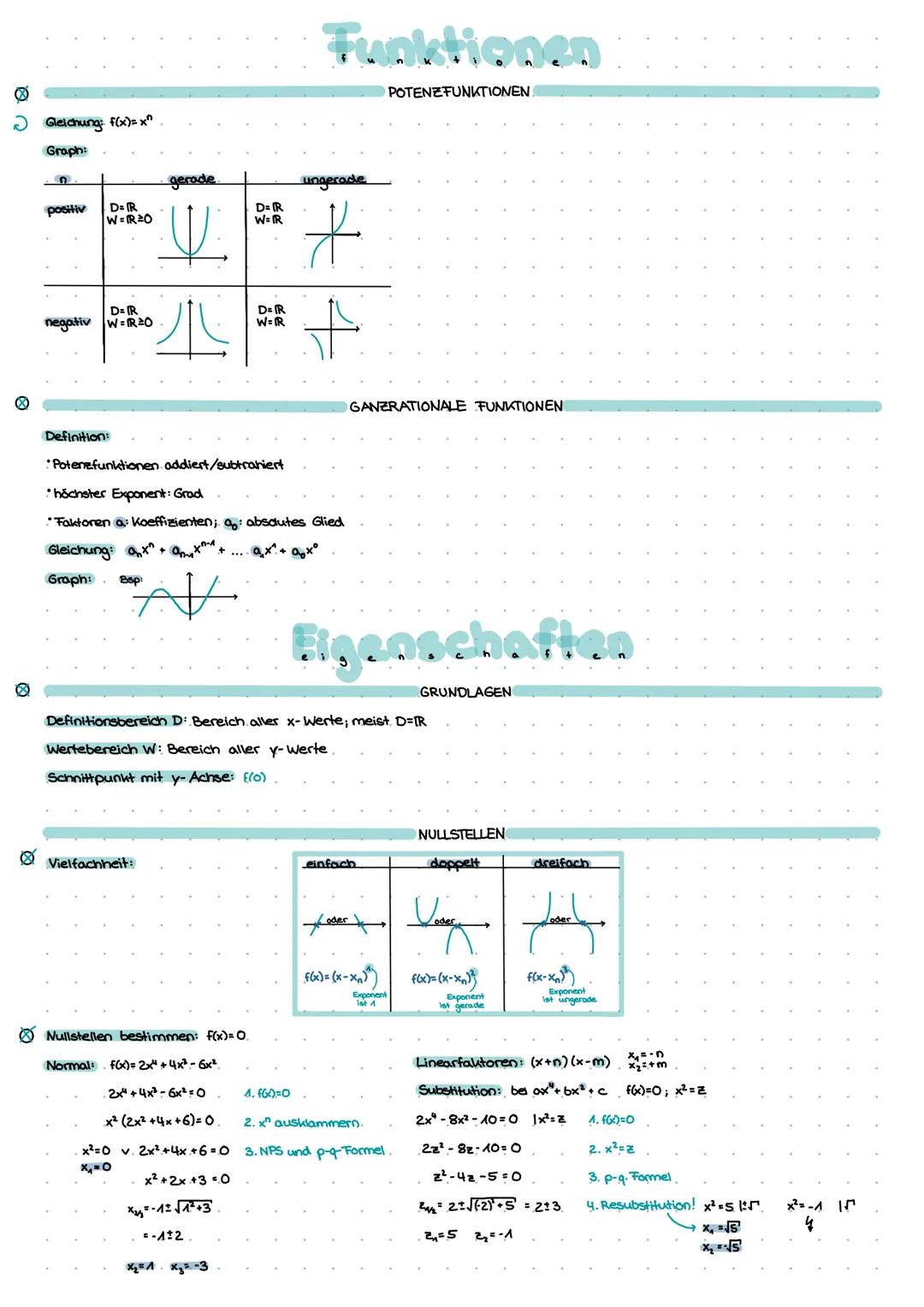
Grafisches Ableiten folgt klaren Regeln: Extrema der ursprünglichen Funktion werden zu Nullstellen der Ableitung, Wendestellen zu Extrema. Steigt f, ist f' positiv - fällt f, ist f' negativ.

Die wichtigsten Ableitungsregeln sind schnell gelernt: Potenzregel f(x) = x^n → f'(x) = n·x^$n-1$, Faktorregel und Summenregel. Konstante Faktoren bleiben stehen, Exponenten "wandern" nach vorn.

Tangenten haben die Steigung f'(x₀) im Berührpunkt. Berechne zuerst die Ableitung, dann die Steigung im gewünschten Punkt, schließlich die Geradengleichung y = mx + b. Normalen stehen senkrecht zur Tangente - ihre Steigung ist -1/f'(x₀).

Den Steigungswinkel findest du mit α = arctan(f'(x₀)). Dein CAS-Rechner macht das automatisch!

Profi-Trick: Bei Ableitungen mit mehreren Variablen bleibt alles stehen, was nicht nach der gewünschten Variable abgeleitet wird!

Kurvendiskussion mit Ableitungen

Monotonie bestimmst du über f'(x): ist f'(x) > 0, steigt die Funktion streng monoton. Berechne die Nullstellen von f', teile den Definitionsbereich in Intervalle und teste je eine Stelle.

Für Extrema brauchst du f'(x) = 0 (notwendige Bedingung) und einen Vorzeichenwechsel von f' (hinreichende Bedingung). Wechsel von + nach - bedeutet Hochpunkt, von - nach + Tiefpunkt. Alternativ nutze f''(x): f''(x) < 0 = Hochpunkt, f''(x) > 0 = Tiefpunkt.

Wendestellen findest du mit f''(x) = 0 und Vorzeichenwechsel von f''. Links-Rechts-Wendepunkte haben praktische Bedeutung: Sie zeigen dir, wo Änderungsraten maximal oder minimal sind - also wo es am steilsten berg-auf oder berg-ab geht!

Krümmung erkennst du an f''(x): f''(x) > 0 bedeutet Linkskrümmung (wie ein Lächeln), f''(x) < 0 Rechtskrümmung.

Klausurtipp: Vergiss nie, die y-Koordinaten durch Einsetzen in f(x) zu berechnen - ohne sie sind deine Punkte unvollständig!

Vektoren im Koordinatensystem

Vektoren beschreiben Richtung und Länge im Raum. Ein Ortsvektor zeigt vom Ursprung zu einem Punkt, ein Verbindungsvektor von einem Punkt zum anderen mit der Formel AB⃗ = B⃗ - A⃗.

Die Länge eines Vektors berechnest du mit |v⃗| = √$x² + y² + z²$ - das ist der 3D-Pythagoras! Addition und Subtraktion funktionieren komponentenweise, Vielfache bildest du durch Multiplikation jeder Komponente.

Kollinearität bedeutet, dass Vektoren parallel sind - einer ist ein Vielfaches des anderen. Prüfe das, indem du schaust, ob r·a⃗ = b⃗ für alle Komponenten das gleiche r ergibt.

Linearkombinationen entstehen, wenn du Vektoren mit verschiedenen Faktoren addierst: r⃗ = s·a⃗ + t·b⃗. Das ist die Basis für Geraden- und Ebenengleichungen!

Visualisierungstipp: Stelle dir Vektoren als Pfeile vor - das macht Richtung und Länge sofort anschaulich!