Grundlagen der Algebra
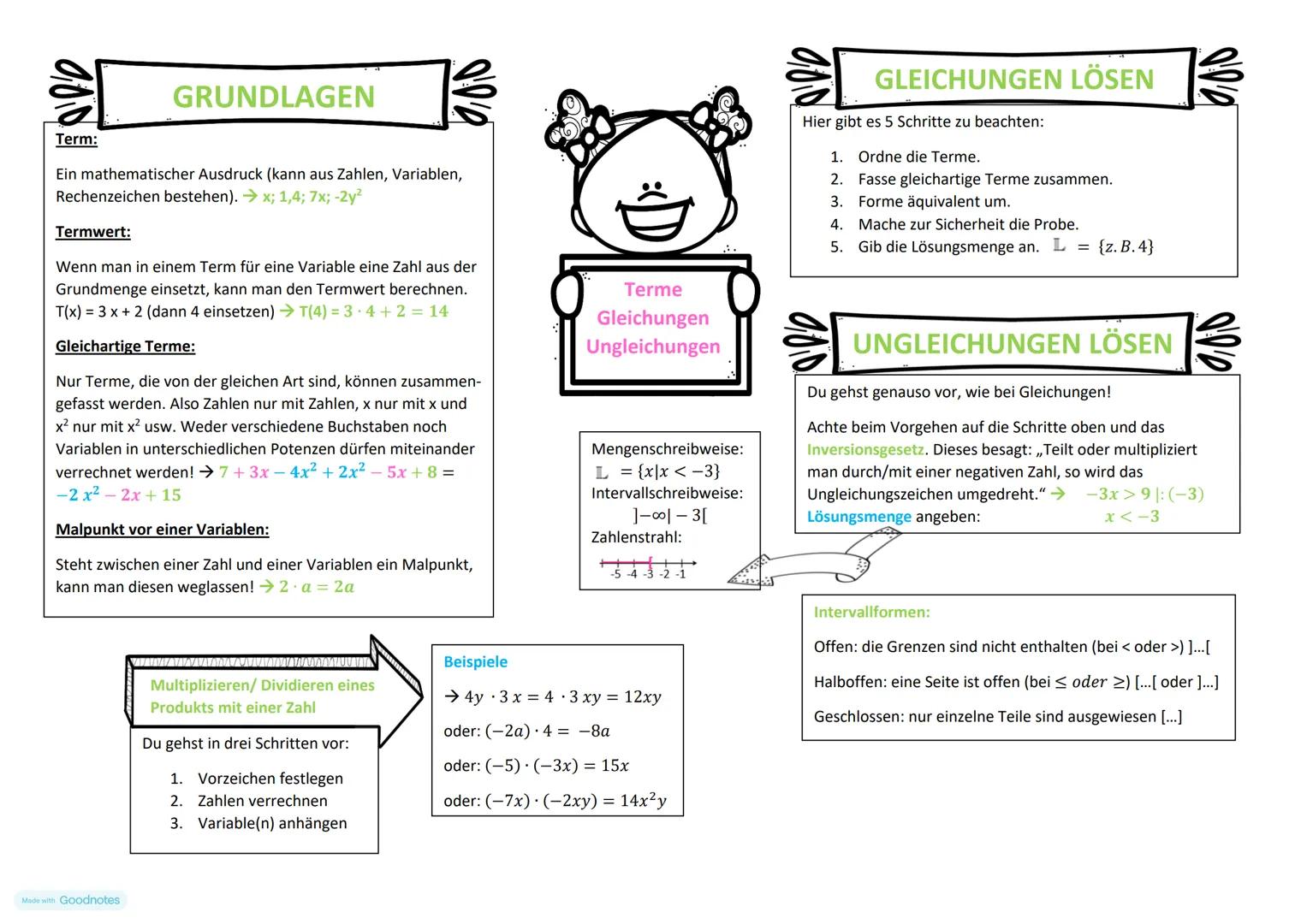
Terme sind mathematische Ausdrücke aus Zahlen, Variablen und Rechenzeichen - wie 7x oder -2y². Du kannst sie dir wie Bausteine vorstellen, die du nach bestimmten Regeln zusammenfügst.
Den Termwert berechnest du, indem du für die Variable eine konkrete Zahl einsetzt. Bei T(x) = 3·x + 2 wird T(4) = 3·4 + 2 = 14. Das ist wie ein Rezept - du tauschst einfach die Zutat aus!
Gleichartige Terme zusammenfassen ist der Schlüssel zum Erfolg. Zahlen nur mit Zahlen, x nur mit x, x² nur mit x². Verschiedene Buchstaben oder Potenzen bleiben getrennt - so wird aus 7 + 3x - 4x² + 2x² - 5x + 8 ganz ordentlich -2x² - 2x + 15.
Merktipp: Den Malpunkt vor Variablen kannst du weglassen - aus 2·a wird einfach 2a!
Gleichungen und Ungleichungen lösen
Gleichungen löst du in 5 klaren Schritten: Terme ordnen, gleichartige zusammenfassen, äquivalent umformen, Probe machen und Lösungsmenge angeben. Diese Reihenfolge ist dein roter Faden durch jede Aufgabe.
Bei Ungleichungen gehst du genauso vor - mit einer wichtigen Ausnahme! Das Inversionsgesetz besagt: Teilst oder multiplizierst du mit einer negativen Zahl, drehst du das Ungleichungszeichen um. Aus -3x > 9 wird durch ÷(-3) dann x < -3.
Lösungsmengen gibst du auf drei Arten an: als Mengenschreibweise L = {x|x < -3}, als Intervall ]-∞; -3[ oder am Zahlenstrahl. Offene Intervalle ]...[ bedeuten "ohne Grenzen", geschlossene [...] "mit Grenzen".
Produktregel: Beim Multiplizieren erst das Vorzeichen festlegen, dann Zahlen verrechnen, danach Variablen anhängen!