Extrempunkte und Wendepunkte berechnen
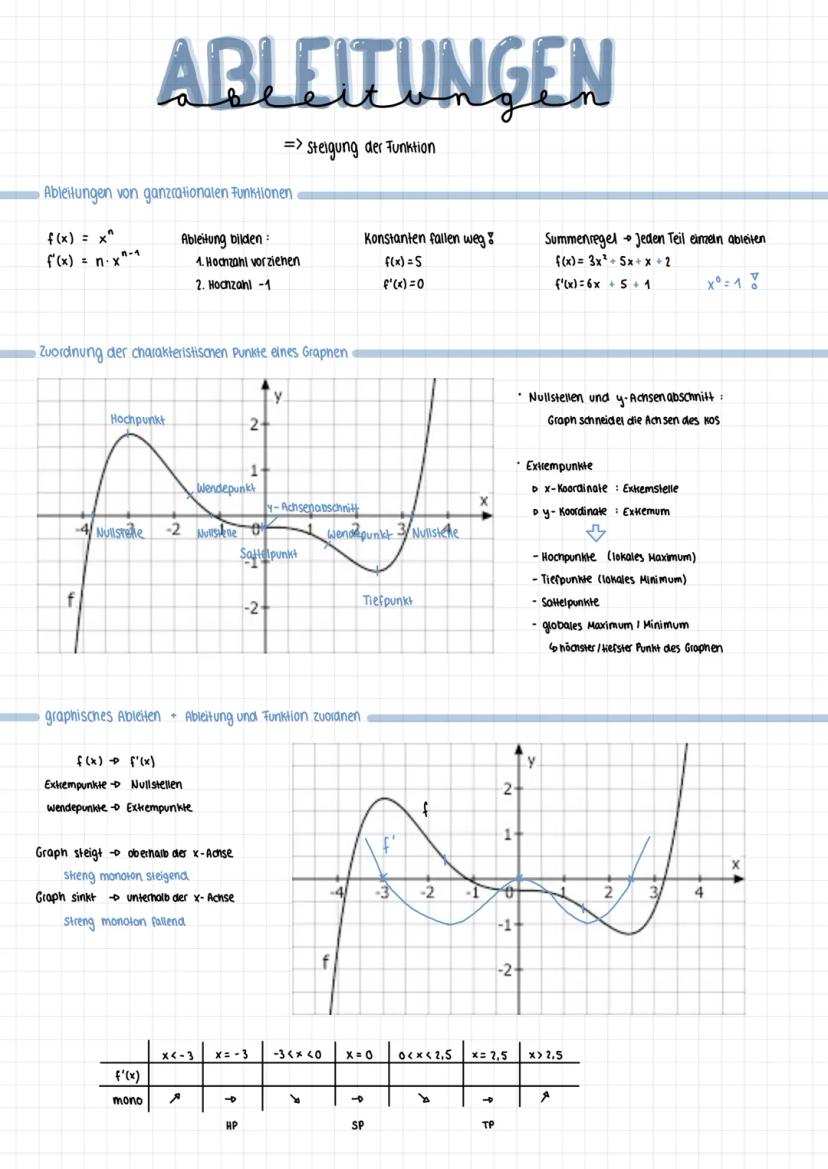
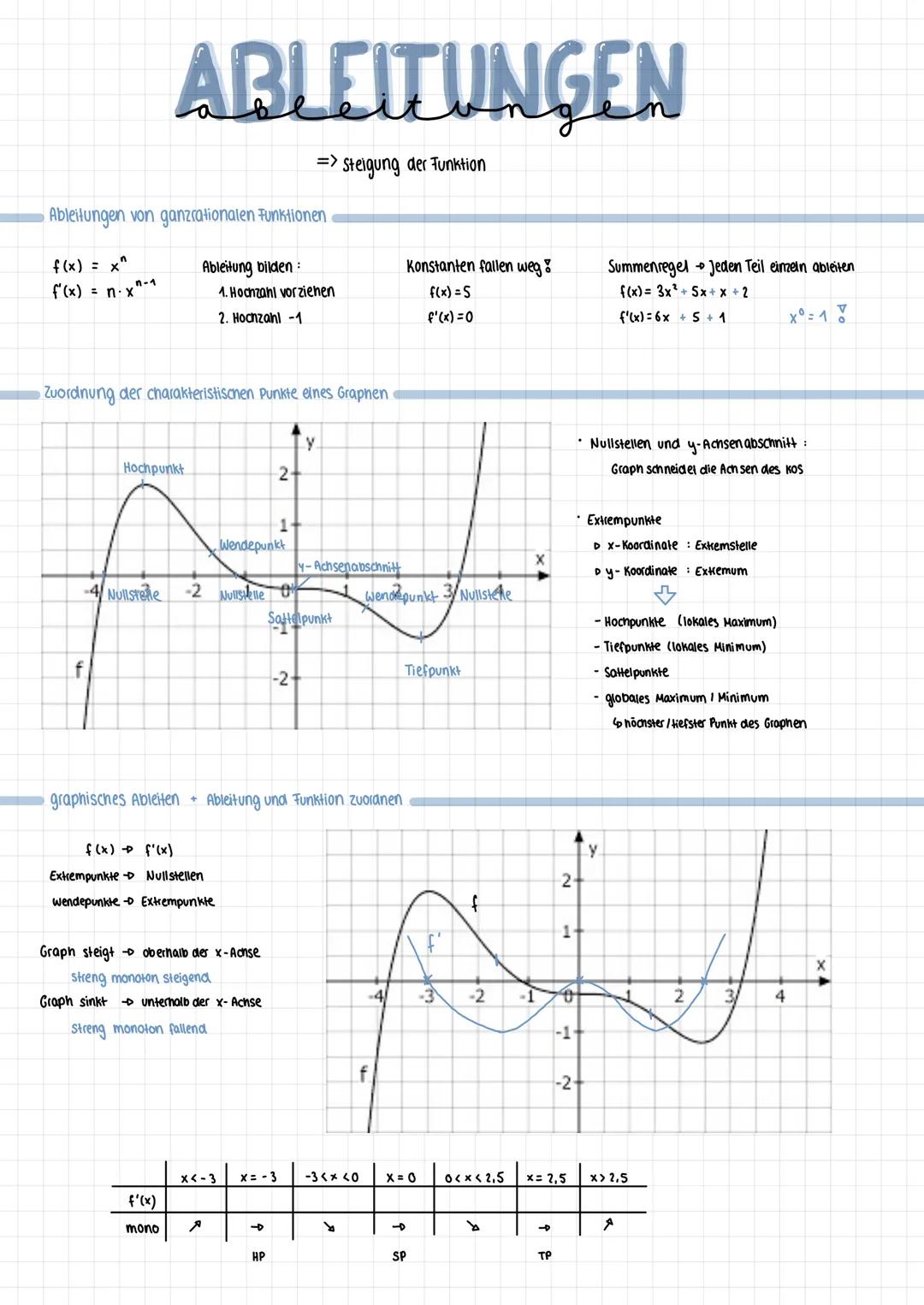
Um Hoch-, Tief- und Sattelpunkte zu finden, gehst du systematisch vor: Erst die Ableitung bilden, dann deren Nullstellen berechnen, und schließlich diese x-Werte in die Ursprungsfunktion einsetzen.
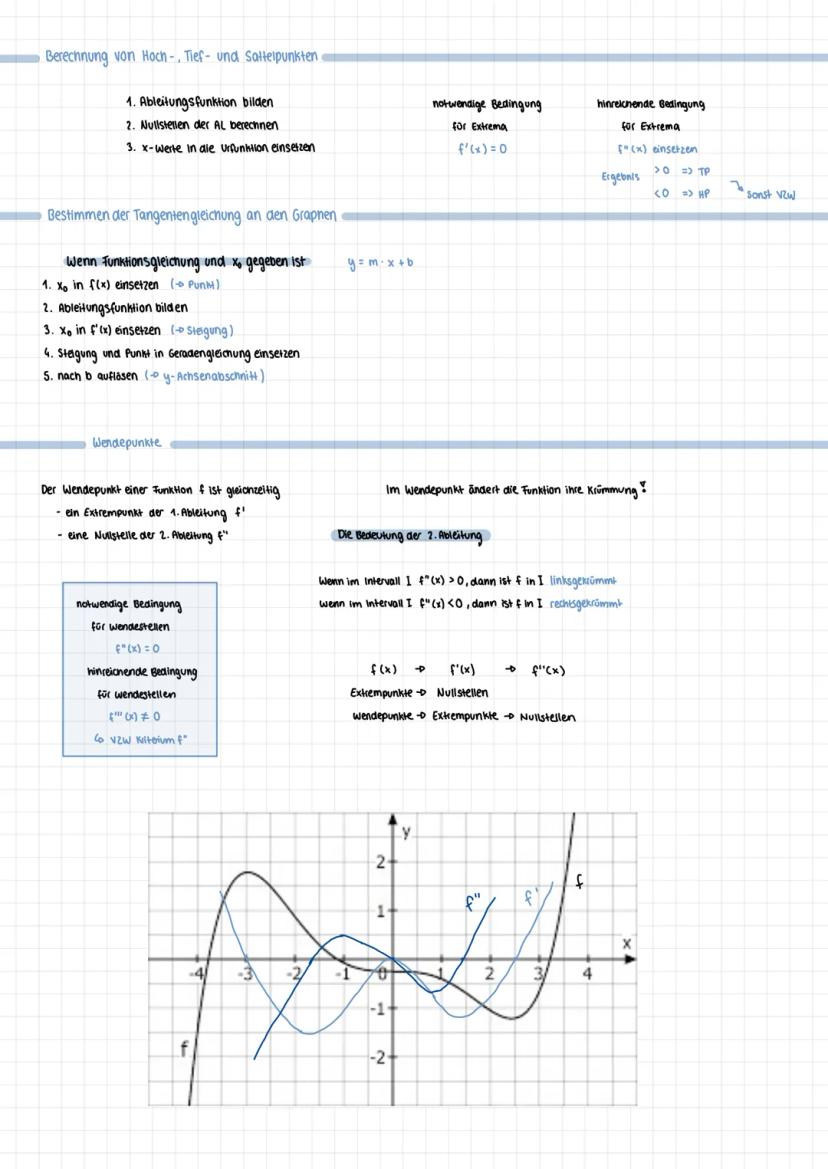
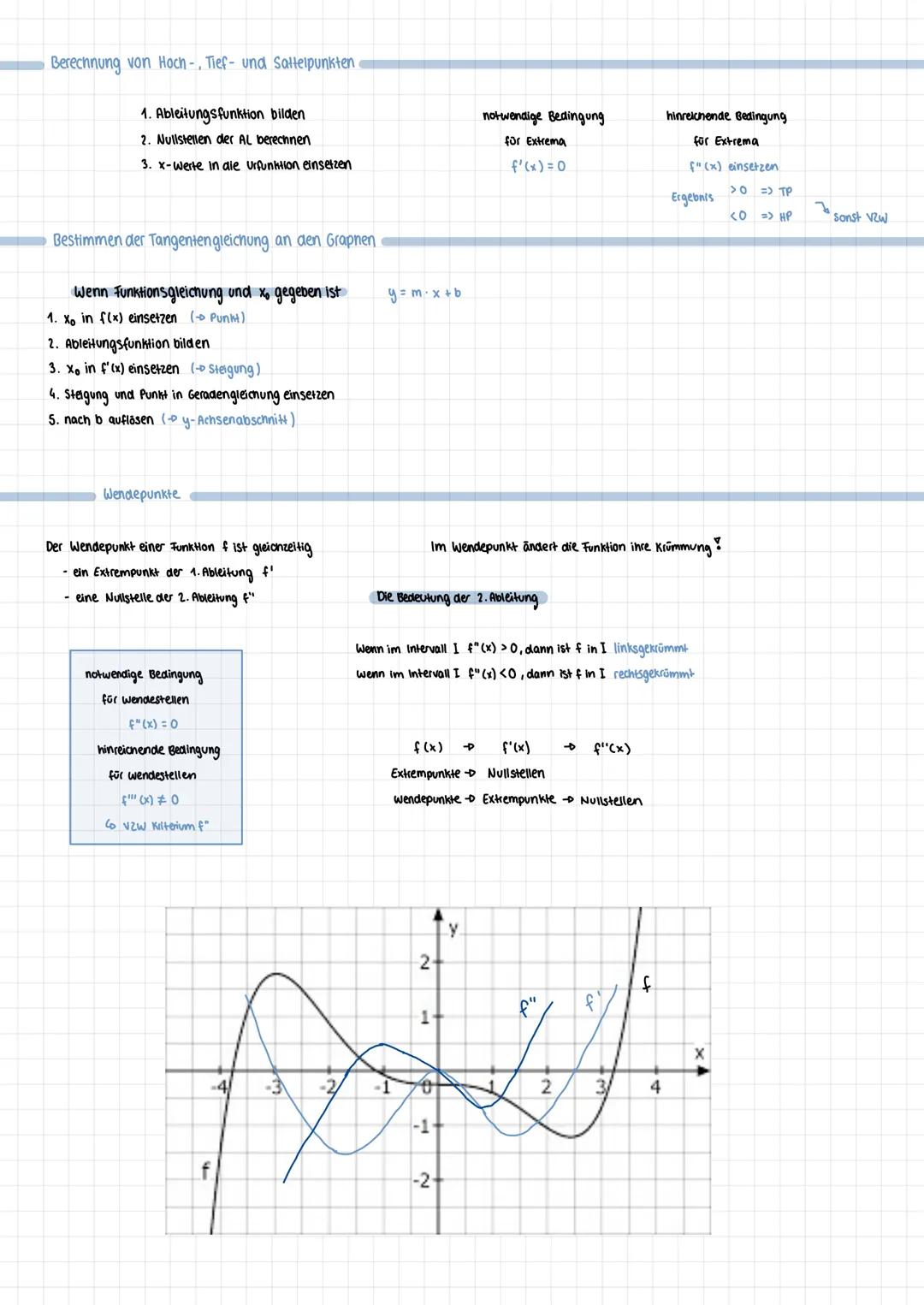
Für die Unterscheidung zwischen Hoch- und Tiefpunkt brauchst du die zweite Ableitung. Die notwendige Bedingung ist f'(x) = 0. Die hinreichende Bedingung prüfst du mit f''(x): Ist das Ergebnis größer als 0, hast du einen Tiefpunkt. Ist es kleiner als 0, einen Hochpunkt.
Wendepunkte findest du über die zweite Ableitung. Dort wo f''(x) = 0 ist, ändert die Funktion ihre Krümmung. Die hinreichende Bedingung erfüllst du, wenn f'''(x) ≠ 0 ist. Im Wendepunkt wechselt die Funktion von links- zu rechtsgekrümmt oder umgekehrt.
Eselsbrücke: f''(x) > 0 bedeutet linksgekrümmt (wie ein lächelnder Mund) → Tiefpunkt möglich!