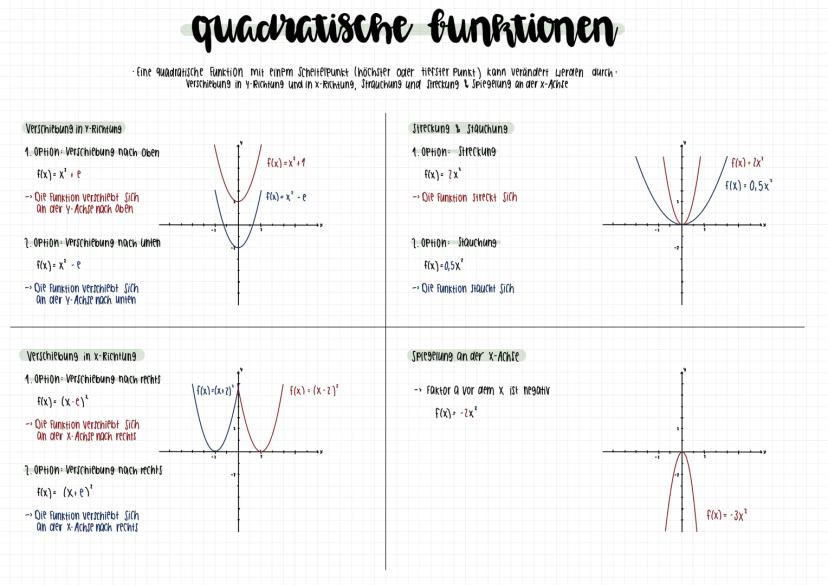
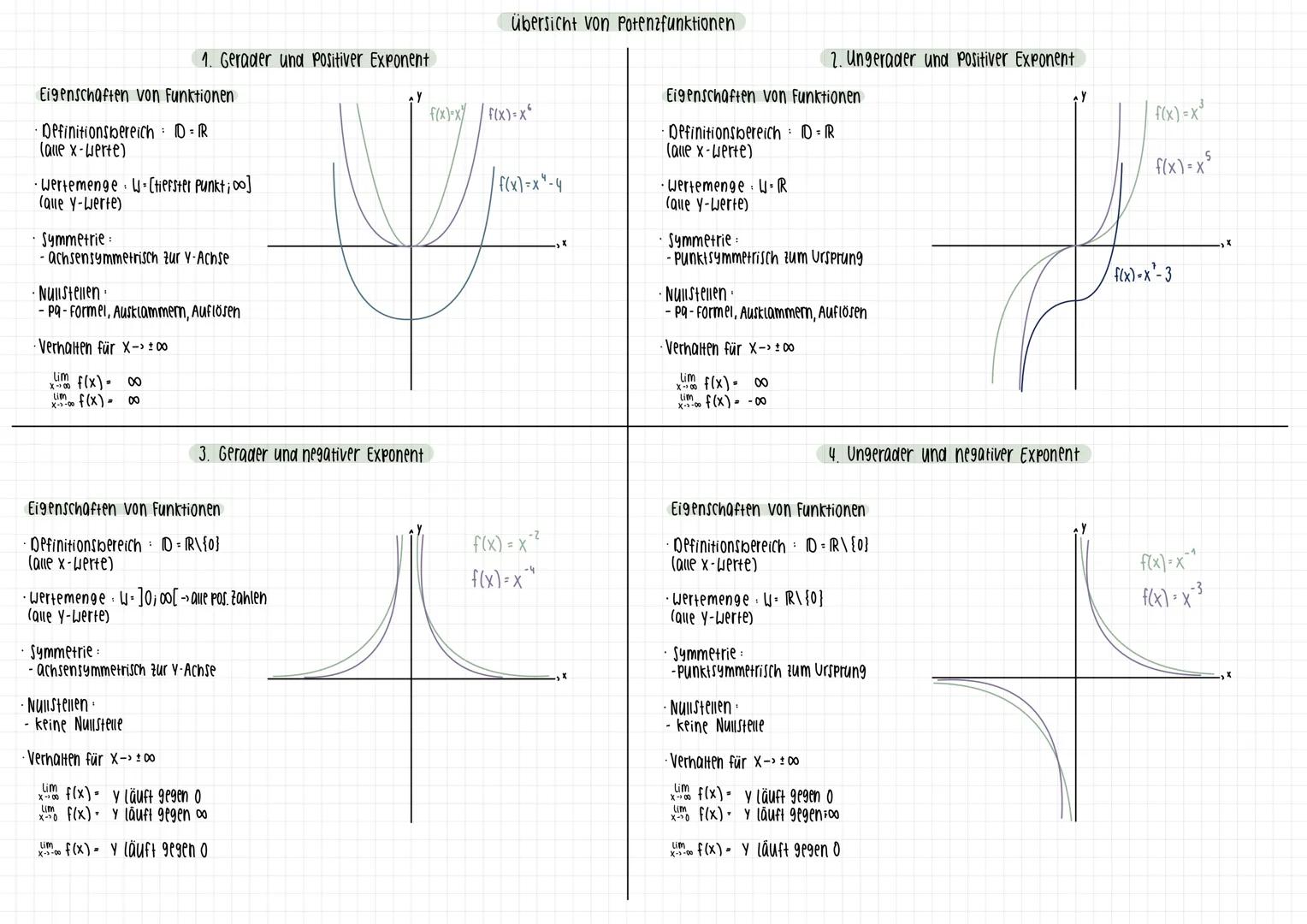
Übersicht von Potenzfunktionen
Potenzfunktionen wie f(x) = x^n verhalten sich ganz unterschiedlich, je nachdem ob der Exponent gerade oder ungerade, positiv oder negativ ist. Diese Übersicht hilft dir, sie schnell zu erkennen!
Gerade, positive Exponenten (x², x⁴): Sehen aus wie ein U, sind achsensymmetrisch zur y-Achse und gehen bei x → ±∞ gegen +∞. Definitionsbereich ist alle reellen Zahlen.
Ungerade, positive Exponenten (x³, x⁵): Sehen aus wie ein S, sind punktsymmetrisch zum Ursprung. Bei x → +∞ gehen sie gegen +∞, bei x → -∞ gegen -∞.
Negative Exponenten (x⁻², x⁻³): Sind Hyperbeln mit Definitionslücke bei x = 0. Gerade Exponenten sind achsensymmetrisch, ungerade punktsymmetrisch. Alle nähern sich für große |x| der x-Achse an.
Faustregel: Gerade Exponenten = U-Form, ungerade Exponenten = S-Form, negative Exponenten = Hyperbel mit Lücke bei x = 0!