Analysis

Analysis ist dein mathematisches Werkzeug, um Funktionen vollständig zu verstehen. Du lernst, wie du Graphen analysierst, ihre besonderen Punkte findest und ihr Verhalten beschreibst.

Das hier ist dein Startpunkt für alle wichtigen Konzepte - von Definitionsmengen über Ableitungen bis hin zu Integralen. Jedes Thema baut auf dem anderen auf, also keine Panik wenn's am Anfang komplex wirkt.

Tipp: Die meisten Aufgaben in Klausuren folgen immer dem gleichen Schema - einmal verstanden, läuft's wie am Schnürchen!

Definitions- und Wertebereich

Die Definitionsmenge (Df) zeigt dir, welche x-Werte überhaupt erlaubt sind. Schreibst du als $Df = \mathbb{R}$ (alle reellen Zahlen) oder $Df = \mathbb{R}\setminus{4}$ (alle außer 4). Bei Wurzelfunktionen wird's spannend: $Df = [-6; \infty)$ bedeutet alle Zahlen ab -6.

Die Wertemenge (Wf) sammelt alle y-Werte, die rauskommen können. Einfach am Graphen ablesen oder rechnerisch bestimmen.

Symmetrie checkst du so: Für Achsensymmetrie zur y-Achse muss $f(-x) = f(x)$ gelten (gerade Funktion). Für Punktsymmetrie zum Ursprung brauchst du $f(-x) = -f(x)$ (ungerade Funktion).

Beim Randverhalten schaust du, was bei sehr großen und sehr kleinen x-Werten passiert. Das bestimmt immer der Term mit der höchsten Potenz. Bei $x \to 0$ ist der Term mit der niedrigsten Potenz der Boss.

Merkhilfe: Gerade Exponenten = Achsensymmetrie, ungerade Exponenten = Punktsymmetrie!

Nullstellen und Ableitungen

Nullstellen findest du mit verschiedenen Tricks: pq-Formel, Ausklammern $x^2+3x = x(x+3) = 0$ oder Substitution bei kniffligen Termen wie $x^4-20x^2+64$. Den y-Achsenabschnitt kriegst du, indem du x=0 einsetzt.

Die wichtigsten Ableitungsregeln sind deine besten Freunde: Potenzregel $x^n \to n \cdot x^{n-1}$, Faktorregel (Konstanten bleiben stehen) und Summenregel (jeden Term einzeln ableiten).

Die momentane Änderungsrate ist einfach die Ableitung an einem Punkt. Die mittlere Änderungsrate berechnest du mit $\frac{f(x_2)-f(x_1)}{x_2-x_1}$ - das ist die Steigung der Sekante zwischen zwei Punkten.

Praxis-Tipp: Konstanten (Zahlen ohne x) fallen beim Ableiten immer weg!

Extrem- und Wendepunkte

Extrempunkte findest du mit dem Standardverfahren: 1. Ableitung bilden, 2. $f'(x) = 0$ setzen (notwendige Bedingung), 3. $f''(x) \neq 0$ prüfen (hinreichende Bedingung), 4. x-Werte in $f(x)$ einsetzen für die y-Koordinaten.

Bei Wendepunkten brauchst du drei Ableitungen: $f''(x) = 0$ und $f'''(x) \neq 0$. Die Wendetangente berechnest du mit $t(x) = mx + n$, wobei $m = f'(x_{WP})$.

Das Krümmungsverhalten liest du an der zweiten Ableitung ab: $f'' < 0$ = rechtsgekrümmt (Hochpunkt), $f'' > 0$ = linksgekrümmt (Tiefpunkt).

Eselsbrücke: Bei Wendepunkten wechselt die Krümmung - wie beim Autofahren von Rechts- in Linkskurve!

Monotonie und Schnittpunkte

Monotonie checkst du mit der ersten Ableitung: $f'(x) > 0$ bedeutet streng monoton steigend, $f'(x) < 0$ bedeutet streng monoton fallend. Such dir die Nullstellen der Ableitung und teste in den Intervallen dazwischen.

Bei Randwerten musst du aufpassen: Manchmal liegt das absolute Maximum nicht am Extrempunkt, sondern am Rand des Definitionsbereichs. Einfach alle Kandidaten in die Ausgangsfunktion einsetzen und vergleichen.

Schnittpunkte zweier Graphen findest du, indem du die Funktionen gleichsetzt: $f(x) = g(x)$, nach x auflöst und dann den y-Wert berechnest.

Wichtig: Bei Randwertproblemen immer alle kritischen Stellen UND die Randpunkte checken!

Steckbriefaufgaben und Extremwertprobleme

Bei Steckbriefaufgaben baust du aus gegebenen Informationen die Funktion zusammen. Funktion 2. Grades hat die Form $ax^2 + bx + c$, 3. Grades $ax^3 + bx^2 + cx + d$. Aus jedem gegebenen Punkt oder jeder Bedingung machst du eine Gleichung, löst das LGS und fertig.

Extremwertprobleme sind dein Praxistest: 1. Hauptbedingung aufstellen (was willst du optimieren?), 2. Nebenbedingungen finden, 3. Zielfunktion bilden (Nebenbedingungen in Hauptbedingung einsetzen), 4. Maximum/Minimum berechnen.

Nützliche Formeln: Flächeninhalt $A = l \cdot b$, Volumen $V = l \cdot b \cdot h$, Umfang $U = 2l + 2b$.

Praxis-Tipp: Bei Extremwertaufgaben immer erst überlegen: Was soll maximal/minimal werden?

Funktionsscharren

Funktionsscharen sind Funktionen mit einem Parameter (meist $a$, $t$ oder ähnlich). Der Parameter ist eine feste Zahl, keine Variable - beim Ableiten behandelst du ihn wie eine Konstante.

Transformationen verändern den Graphen: $a(x-c)^2 + b$ streckt/staucht (durch $a$), verschiebt auf der x-Achse (durch $c$) und auf der y-Achse (durch $b$).

Bei der Berechnung von Extrempunkten können Fallunterscheidungen nötig werden. Wenn $f''(x) = 6a$ rauskommt, musst du prüfen: Für $a > 0$ ist $6a > 0$(Tiefpunkt), für$a < 0$ist$6a < 0$ (Hochpunkt).

Achtung: Parameter sind Zahlen, nicht Variablen - das vergisst man leicht beim Ableiten!

Mathematische Grundlagen

Bruchrechnung läuft so: Addition/Subtraktion braucht gleichen Nenner, bei Multiplikation rechnest du Zähler mal Zähler und Nenner mal Nenner. Division bedeutet mit dem Kehrbruch multiplizieren.

Die wichtigsten geometrischen Formeln: Quadrat $A = a^2$, Rechteck $A = a \cdot b$, Dreieck $A = \frac{a \cdot h}{2}$, Kreis $A = \pi r^2$. Der Satz des Pythagoras $a^2 + b^2 = c^2$ ist bei rechtwinkligen Dreiecken dein Retter.

Diese Basics brauchst du ständig in der Analysis - besonders bei Extremwertproblemen und Flächenberechnungen.

Grundregel: Solide Basics sparen dir später viel Zeit und Nerven!

Integrale

Ober- und Untersummen sind dein Einstieg ins Integrieren. Du teilst die Fläche in Rechtecke und addierst sie - je mehr Rechtecke, desto genauer wird's. Die Näherung berechnest du als $\frac{U_n + O_n}{2}$.

Ein Integral schreibst du als $\int_a^b f(x)dx$, wobei $a$ die untere und $b$ die obere Grenze ist. Die Stammfunktion $F(x)$ ist das Gegenteil der Ableitung: $F'(x) = f(x)$.

Stammfunktionen bilden: Aus $f(x) = ax^n$ wird $F(x) = \frac{a}{n+1}x^{n+1}$. Der Hauptsatz sagt: $\int_a^b f(x)dx = F(b) - F(a)$.

Merksatz: Integrieren ist das Gegenteil von Ableiten - wie rückwärts fahren!

Integration in der Praxis

Wenn das Integralergebnis bekannt ist und du die Grenzen suchst, stellst du eine Gleichung auf: $\int_1^z 4x , dx = 30$ wird zu $[2x^2]_1^z = 30$, dann $2z^2 - 2 = 30$ lösen.

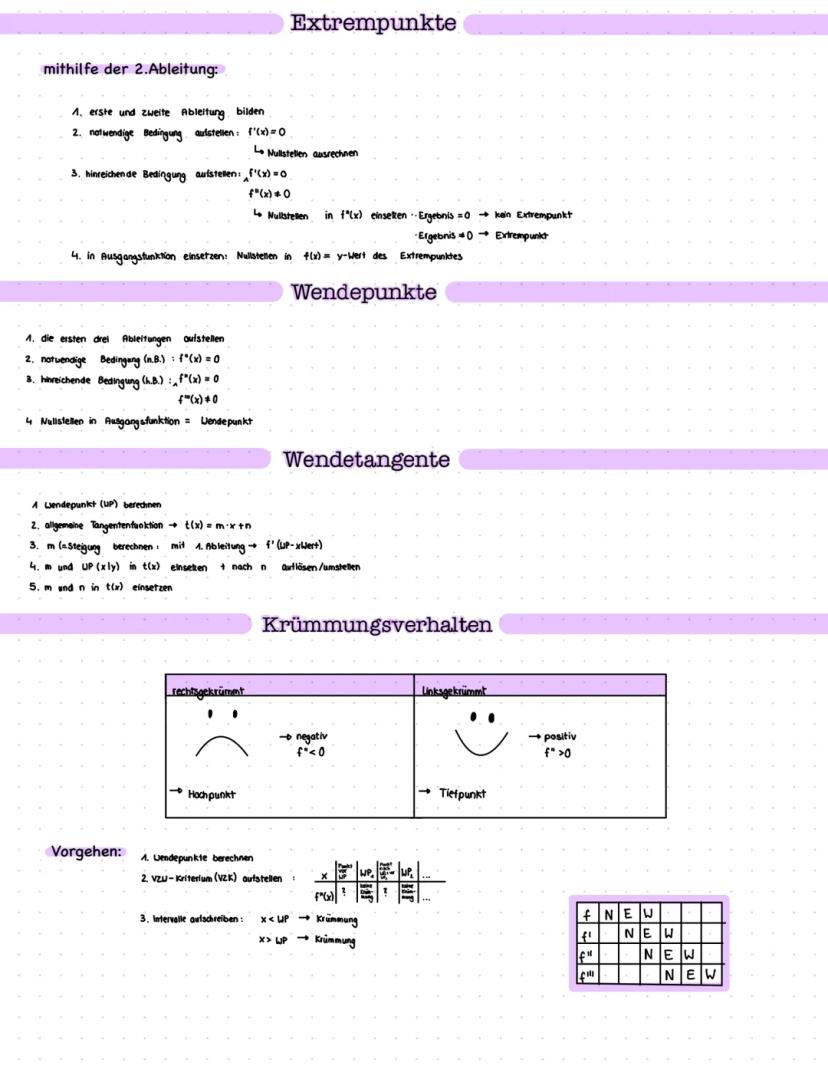
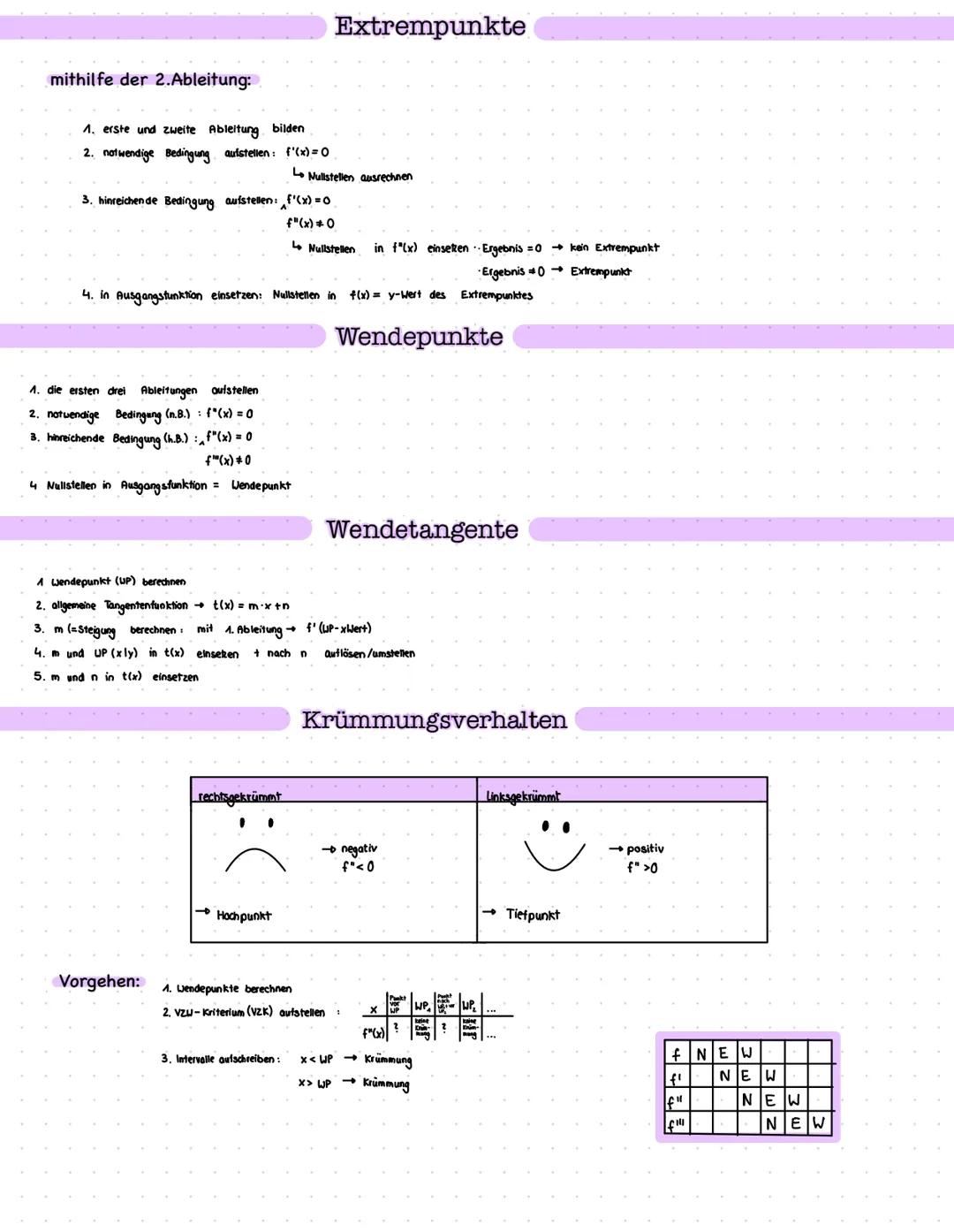
Funktionsuntersuchungen kombinieren alles: Nullstellen, Extrempunkte, Wendepunkte, Monotonie und Krümmung. Das ist dein Komplettpaket für jede Klausur.

Bei Sachkontexten denkst du immer daran: Je kleiner die Intervalle beim Integrieren, desto genauer das Ergebnis.

Klausur-Tipp: Funktionsuntersuchungen folgen immer dem gleichen Schema - einmal gelernt, immer anwendbar!