Mathematik

Flächenberechnungsmethoden mit Integralen

Integral

Mathe1.682 aufrufe·Aktualisiert 27. Juni 2026·12 Seiten

Grundlagen der Integralrechnung: Vorbereitung für die Klausur

sophia@sophiabdrn

Zu Google-Quellen hinzufügen

Integralrechnung ist ein mächtiges Tool, um aus Änderungsraten wieder die...

1 / 10

of 10

# mathe

rekonstruktion von beständen

Laus der Änderungsrate

f(x14

flal

f(x)

f(6)

-die Änderungsrate f(x) ist gegeben

gesucht ist die

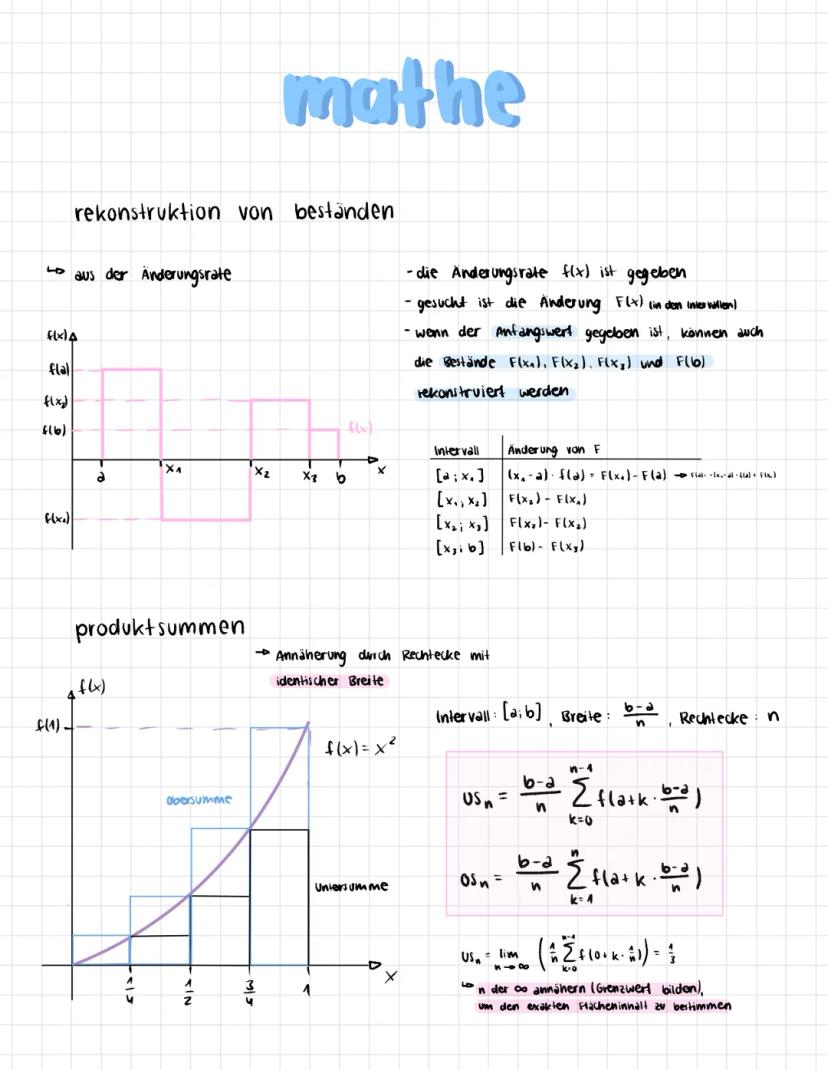
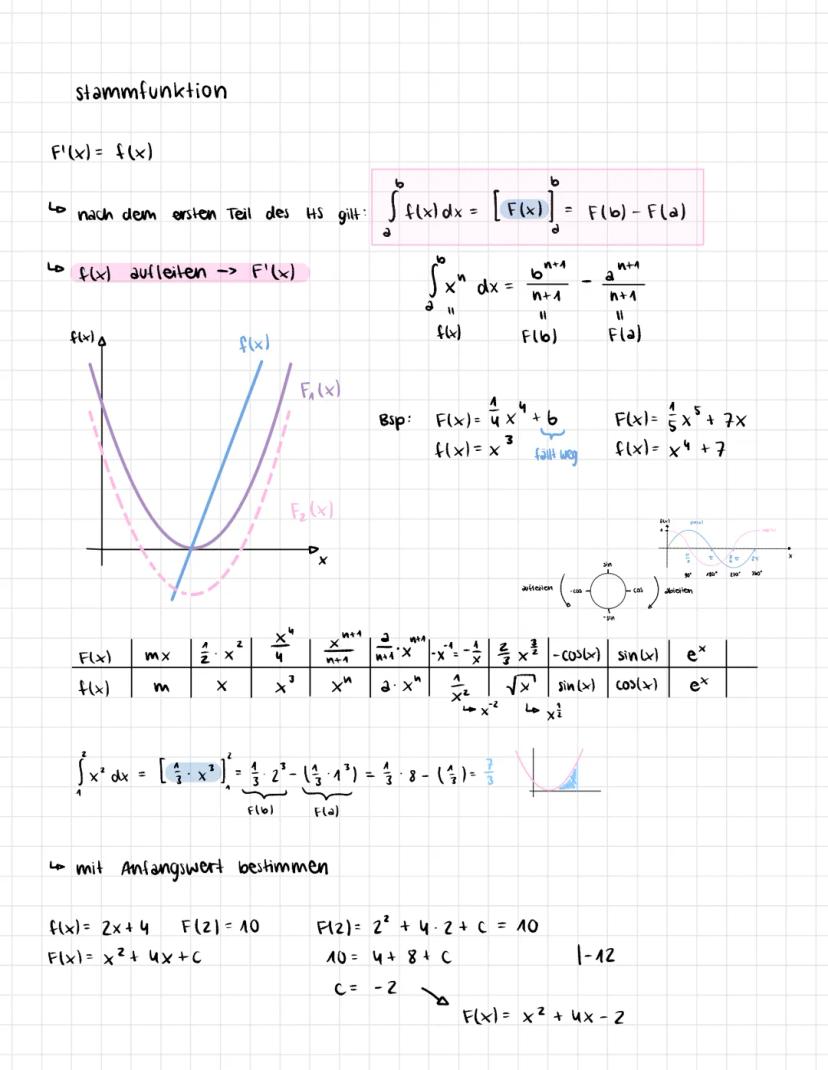
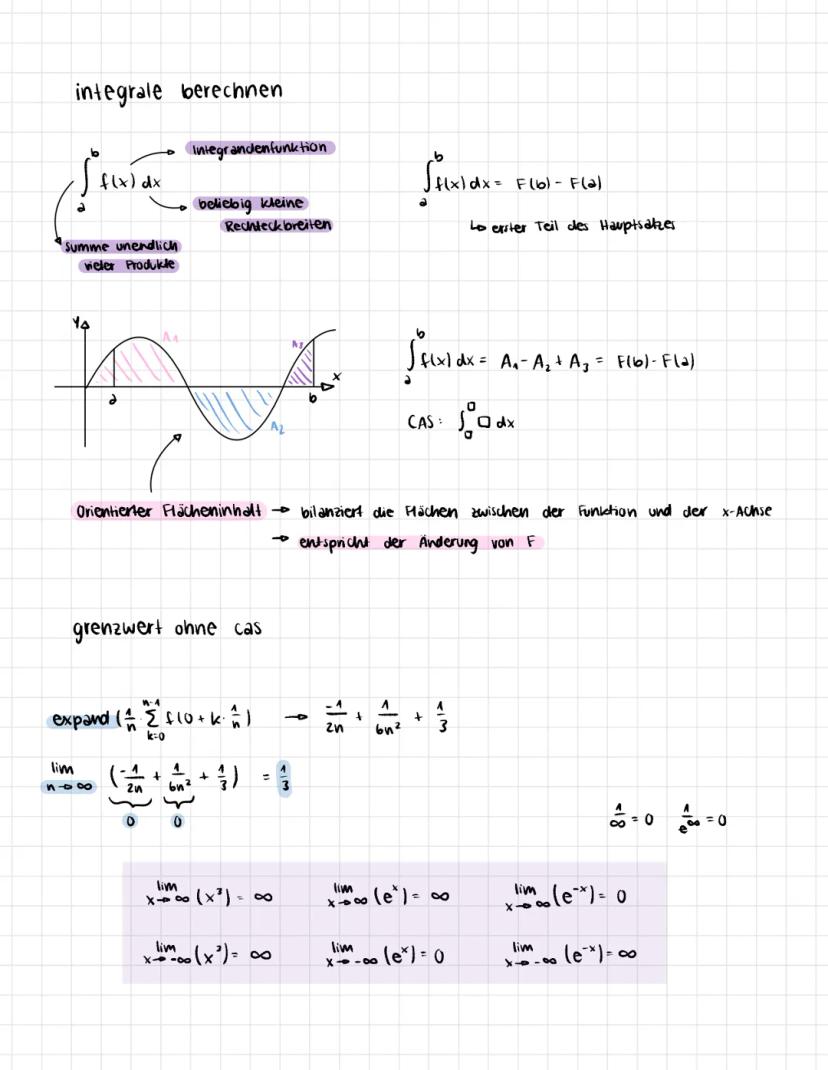
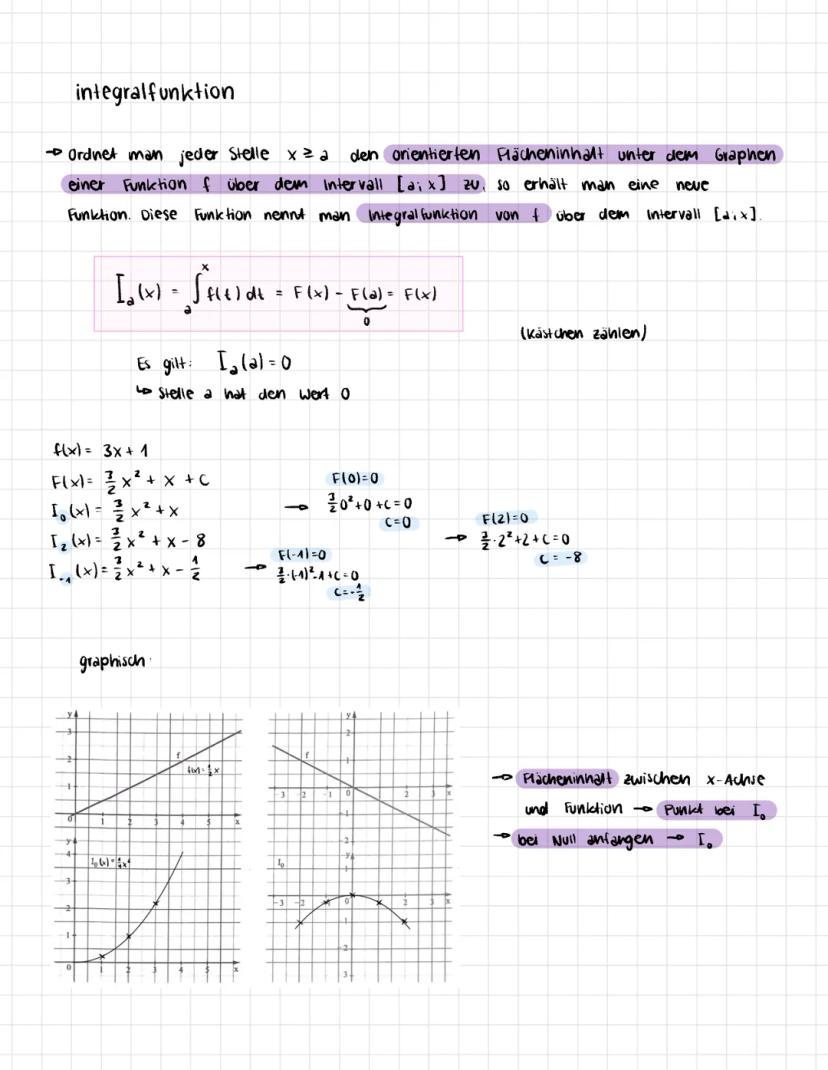
Rekonstruktion von Beständen aus Änderungsraten

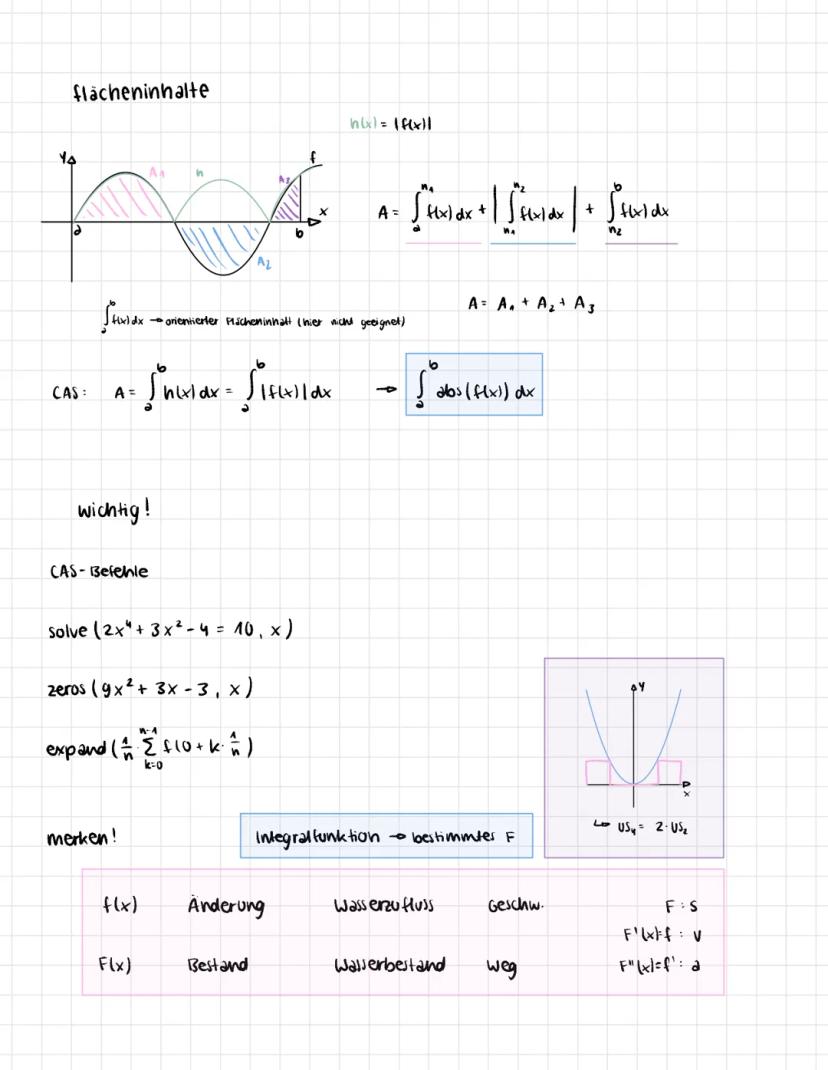
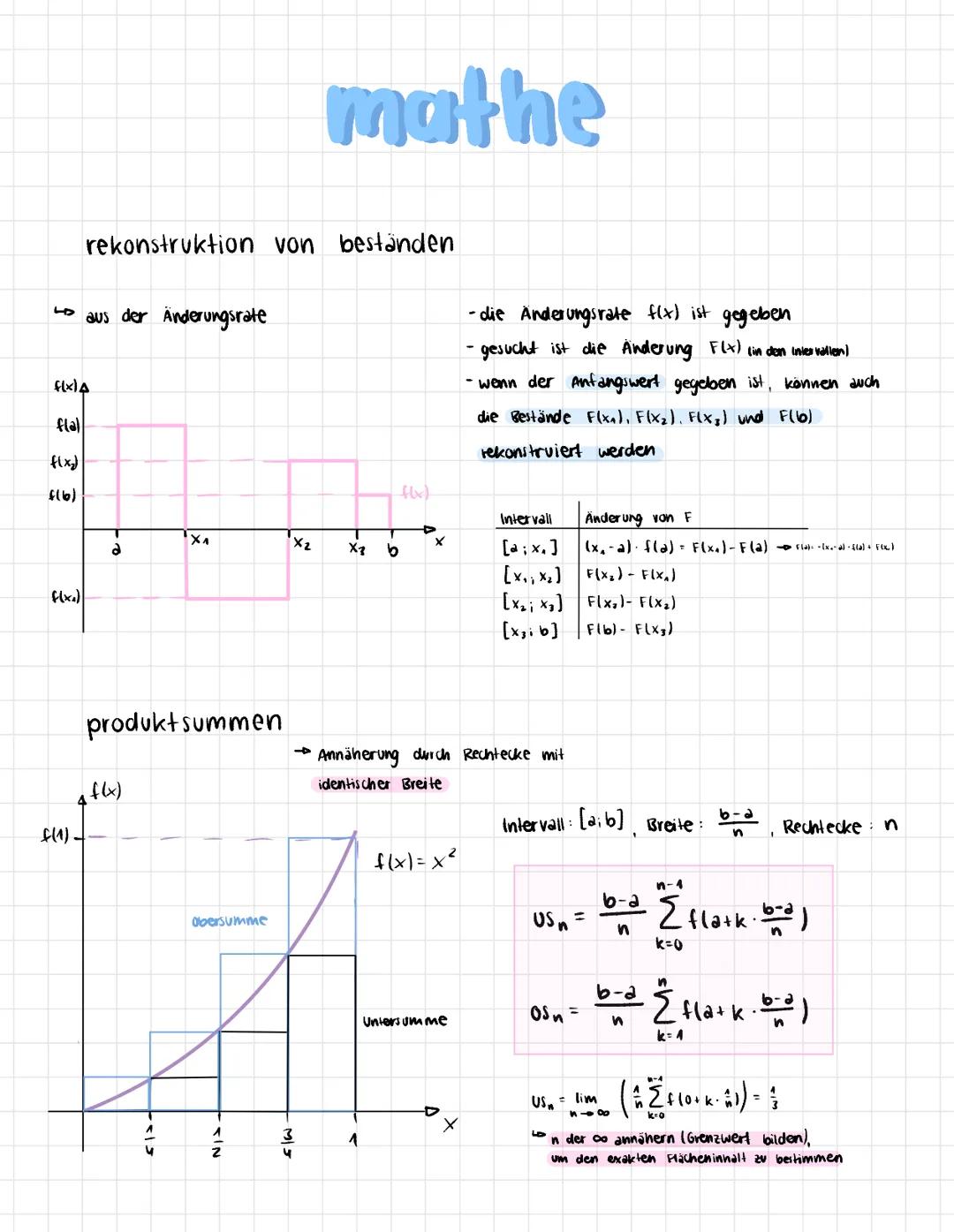
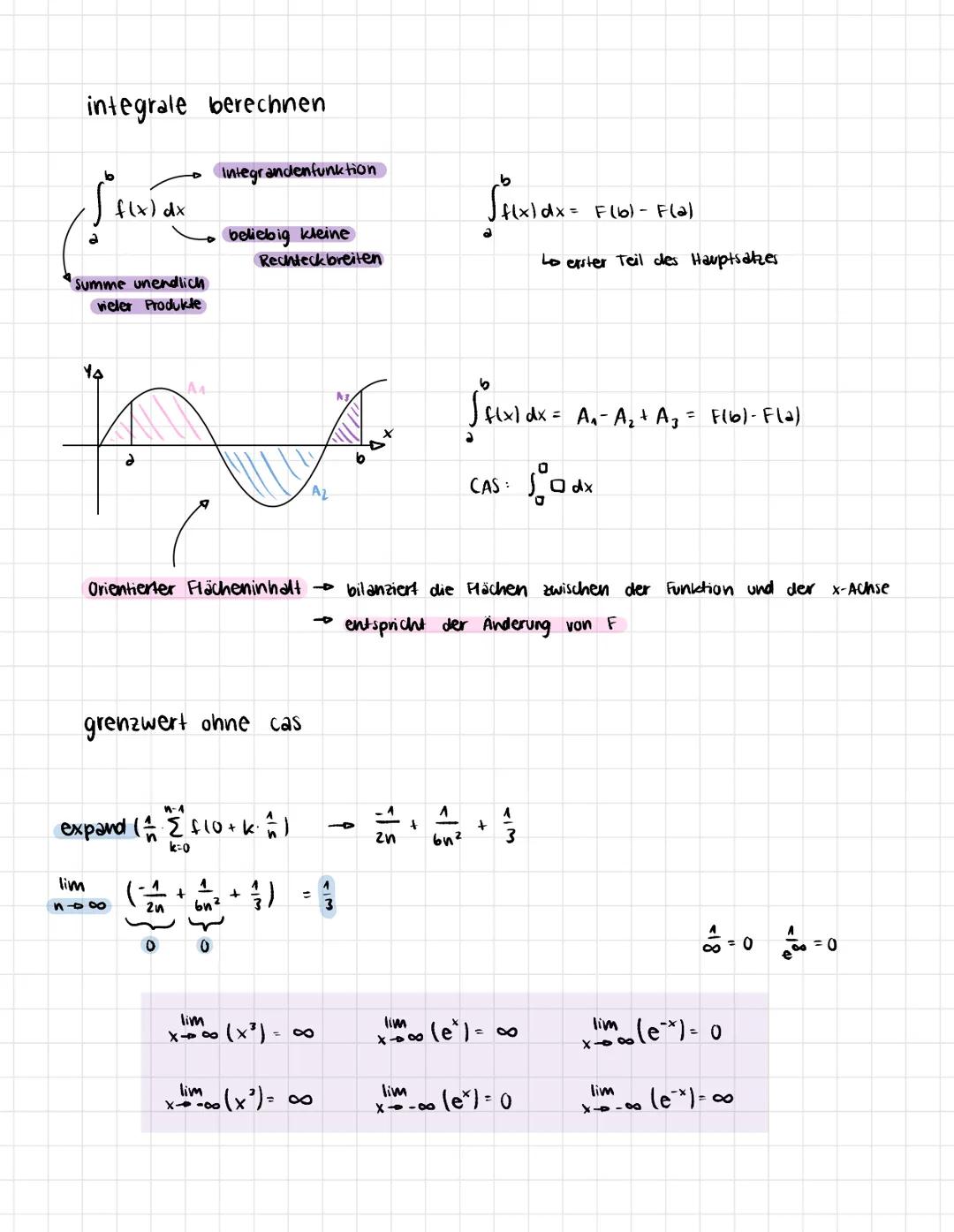
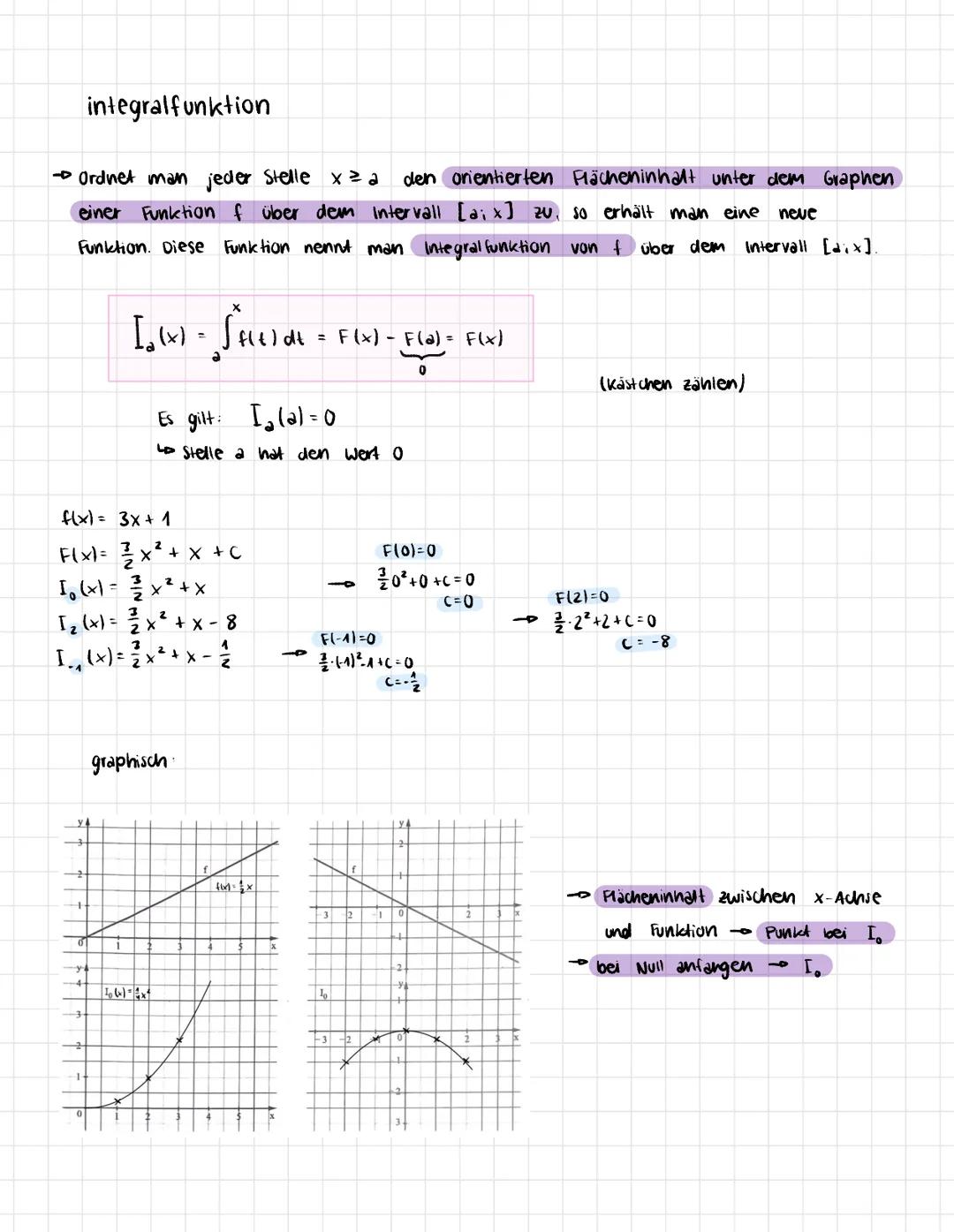
Stell dir vor, du kennst nur die Änderungsrate einer Größe, willst aber den tatsächlichen Bestand wissen. Genau das macht die Integralrechnung möglich! Wenn du zum Beispiel weißt, wie schnell Wasser in einen Tank fließt, kannst du berechnen, wie viel insgesamt drin ist.

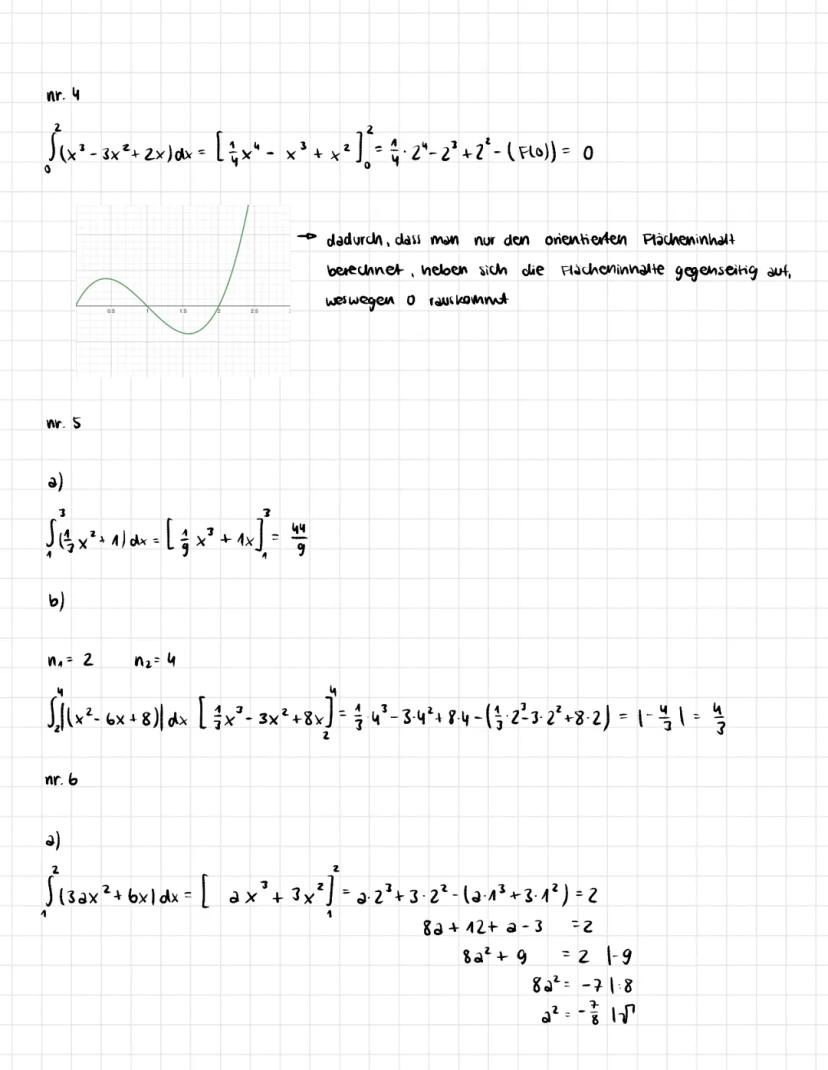
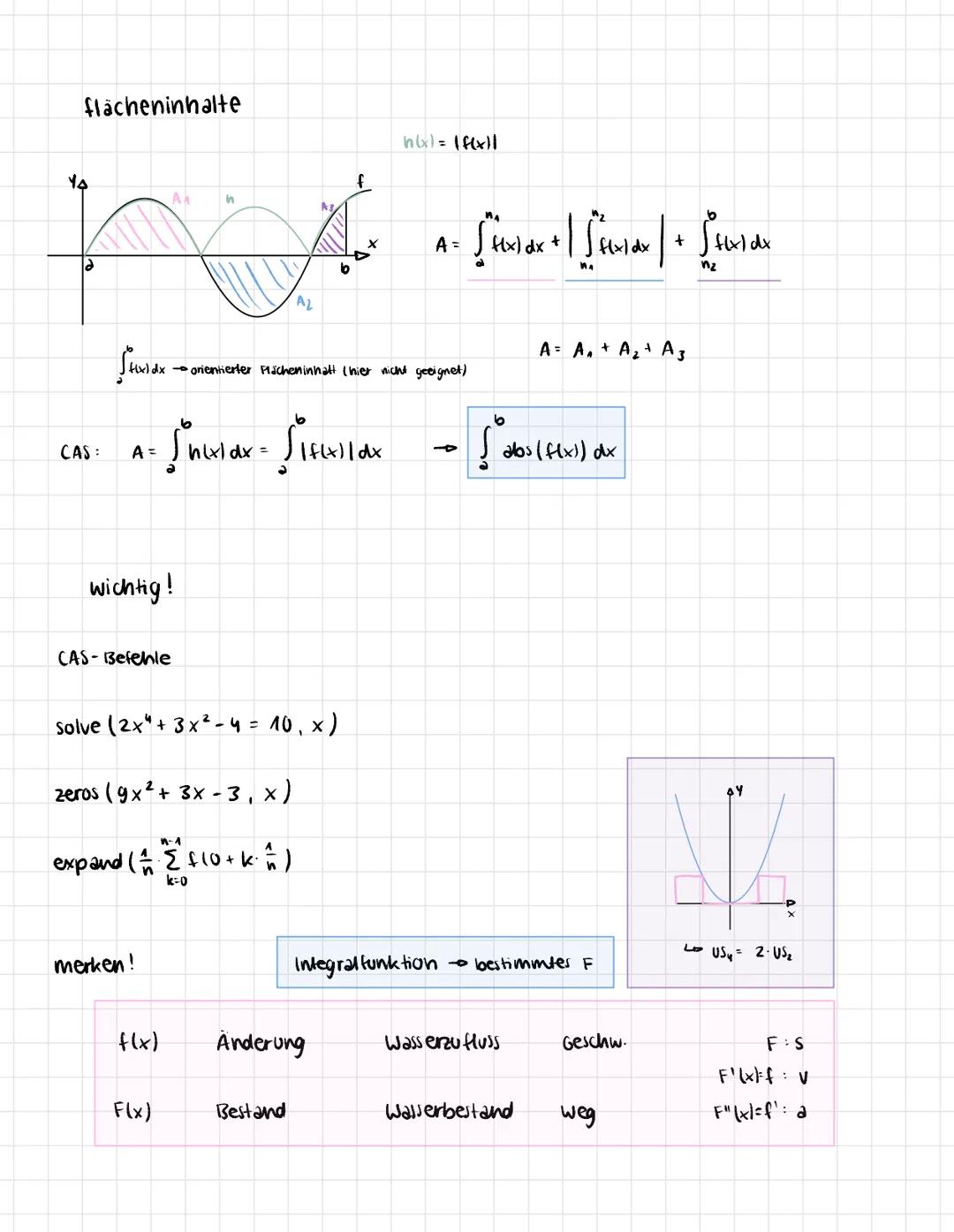
Das Grundprinzip funktioniert über Produktsummen: Du zerlegst das Intervall in kleine Rechtecke und addierst deren Flächen. Die Untersumme $US_n$ und Obersumme $OS_n$ nähern sich immer mehr an den echten Wert an, je mehr Rechtecke du verwendest.

Die Formeln sehen kompliziert aus, aber das Konzept ist einfach: $US_n = \frac{b-a}{n} \sum_{k=0}^{n-1} f(a+k\frac{b-a}{n})$ . Hier teilst du das Intervall $[a;b]$ in $n$ gleiche Teile und berechnest die Rechteckflächen.

Merke dir: Je kleiner die Rechtecke werden (n gegen unendlich), desto genauer wird dein Ergebnis!

of 10

Stammfunktionen und der Hauptsatz

Die Stammfunktion $F(x)$ ist das Gegenteil der Ableitung: Wenn $F'(x) = f(x)$ , dann ist $F$ die Stammfunktion von $f$ . Das ist wie rückwärts rechnen - statt abzuleiten, "leitest du auf".

Der Hauptsatz der Differential- und Integralrechnung macht alles einfacher: $\int_a^b f(x)dx = F(b) - F(a)$ . Statt mühsam unendlich viele Rechtecke zu berechnen, findest du die Stammfunktion und setzt die Grenzen ein.

Bei der Aufleitung merkst du dir die wichtigste Regel: $\int x^n dx = \frac{x^{n+1}}{n+1} + C$ . Das $C$ ist die Integrationskonstante - die brauchst du immer, außer bei bestimmten Integralen.

Praxis-Tipp: Wenn du einen Anfangswert hast, kannst du $C$ bestimmen und die komplette Bestandsfunktion rekonstruieren!

of 10

Integrale berechnen und verstehen

Ein bestimmtes Integral $\int_a^b f(x)dx$ berechnet den orientierten Flächeninhalt zwischen der Funktion und der x-Achse. "Orientiert" bedeutet: Flächen unter der x-Achse zählen negativ, die darüber positiv.

Die praktische Berechnung läuft über $\int_a^b f(x)dx = F(b) - F(a)$ . Du findest die Stammfunktion, setzt die obere Grenze ein, ziehst die untere ab - fertig!

Ohne CAS musst du manchmal Grenzwerte berechnen. Das kann knifflig werden, aber die Grundidee bleibt gleich: Du näherst dich mit immer kleineren Rechtecken dem exakten Wert an.

Wichtig: Grenzwerte wie $\lim_{n \to \infty} \frac{1}{n} = 0$ helfen dir beim Vereinfachen komplexer Ausdrücke!

of 10

Integrationsregeln - Deine Rechenwerkzeuge

Die Integrationsregeln machen dein Leben deutlich einfacher. Du kannst Konstanten vor das Integral ziehen: $\int k \cdot f(x)dx = k \int f(x)dx$ . Integrale addieren sich: $\int (f(x) + g(x))dx = \int f(x)dx + \int g(x)dx$ .

Eine super praktische Regel: $\int_a^b f(x)dx = -\int_b^a f(x)dx$ . Wenn du die Grenzen vertauschst, ändert sich das Vorzeichen. Das hilft oft beim Rechnen!

Bei Integralgrenzen bestimmen setzt du das Integral gleich einem gegebenen Wert und löst nach der gesuchten Grenze auf. Das kann zu mehreren Lösungen führen - prüfe immer, welche sinnvoll sind.

Rechentrick: Bei $\int_a^a f(x)dx = 0$ - wenn Anfang und Ende gleich sind, ist das Integral immer null!

of 10

Integralfunktionen verstehen

Eine Integralfunktion $I_a(x) = \int_a^x f(t)dt$ ordnet jeder Stelle $x$ den Flächeninhalt vom Startpunkt $a$ bis zu dieser Stelle zu. Sie startet immer bei null: $I_a(a) = 0$ .

Je nachdem, wo du startest ( $I_0$ , $I_2$ , $I_{-1}$ ), bekommst du verschiedene Funktionen. Sie unterscheiden sich nur durch eine Konstante - die Form bleibt gleich.

Graphisch entspricht die Integralfunktion der kumulierten Fläche unter der ursprünglichen Kurve. Wenn $f(x)$ die Geschwindigkeit ist, gibt $I_a(x)$ den zurückgelegten Weg an.

Visualisierung hilft: Stell dir vor, du sammelst kontinuierlich Fläche unter der Kurve - das ist deine Integralfunktion!

of 10

Flächeninhalte richtig berechnen

Für echte Flächeninhalte (immer positiv!) musst du aufpassen: Der orientierte Flächeninhalt kann negativ werden. Deshalb brauchst du $\int_a^b |f(x)|dx$ - die Betragsfunktion macht alles positiv.

Praktisch bedeutet das: Finde die Nullstellen der Funktion, teile das Intervall dort auf und berechne jeden Abschnitt einzeln. Dann addierst du die Beträge: $A = |A_1| + |A_2| + |A_3|$ .

Im CAS kannst du direkt ∫|f(x)|dx oder ∫abs(f(x))dx eingeben. Das spart dir die mühsame Aufteilung in Teilintervalle.

CAS-Befehle merken: solve() für Gleichungen, zeros() für Nullstellen, expand() für Grenzwerte - diese drei brauchst du ständig!

of 10

Übungen und Stammfunktionen finden

Beim Aufleiten wendest du die Potenzregel rückwärts an: Aus $x^4$ wird $\frac{x^5}{5} + C$ . Bei $2x^3 - x + 3$ leitest du jeden Term einzeln auf: $\frac{x^4}{2} - \frac{x^2}{2} + 3x + C$ .

Für Brüche schreibst du sie als negative Potenzen: $\frac{6}{x^2} = 6x^{-2}$ wird zu $-6x^{-1} = -\frac{6}{x} + C$ . Bei Exponentialfunktionen bleibt die Form: $\int e^x dx = e^x + C$ .

Trigonometrische Funktionen haben ihre eigenen Regeln: $\int \sin(x) dx = -\cos(x) + C$ . Bei zusammengesetzten Funktionen wie $\sin(\pi x + \pi)$ musst du durch die innere Ableitung teilen.

Immer dran denken: Das $+C$ bei unbestimmten Integralen nie vergessen - sonst sind Punkte weg!

of 10

Bestimmte Integrale berechnen

Bei bestimmten Integralen setzt du die Grenzen in die Stammfunktion ein: $[F(x)]_a^b = F(b) - F(a)$ . Rechne immer sorgfältig - ein Vorzeichenfehler ruiniert das ganze Ergebnis.

Manchmal ist das Ergebnis null, obwohl die Funktion nicht konstant ist. Das liegt am orientierten Flächeninhalt: Positive und negative Bereiche heben sich gegenseitig auf.

Bei Parametern im Integral setzt du alles normal ein und löst dann nach dem Parameter auf. Das führt oft zu quadratischen Gleichungen mit mehreren Lösungen.

Kontroll-Tipp: Skizziere die Funktion! So siehst du sofort, ob dein Ergebnis plausibel ist oder ob sich Bereiche aufheben.

of 10

Anwendungen in Sachaufgaben

Realitätsbezogene Aufgaben zeigen, wofür Integrale wirklich gut sind. Eine Zuflussrate $f(t) = 9 - 0{,}01t^2$ wird zu einer Wassermenge durch Integration.

Die Stammfunktion $F(t) = 9t - 0{,}00333t^3$ gibt die gesamte Wassermenge an. Mit Anfangsbedingungen bestimmst du die Konstante $C$ - oft ist das der Anfangsbestand.

Bei Integralfunktionen in Sachkontexten interpretierst du das Ergebnis: $I_0(x)$ könnte die "seit Zeitpunkt 0 geflossene Wassermenge" bedeuten.

Einheiten beachten: Wenn $f$ in Liter/Minute gegeben ist, hat $\int f(t)dt$ die Einheit Liter - das hilft beim Verständnis!

of 10

Integralfunktionen interpretieren

Eine Integralfunktion $I_0(x) = \int_0^x f(t)dt$ sammelt kontinuierlich die "Effekte" der Funktion $f$ von 0 bis $x$ . Je nach Kontext kann das Wasser, Strecke oder Energie sein.

Die physikalische Bedeutung ist entscheidend: Ist $f(x)$ eine Geschwindigkeit, dann ist $I_0(x)$ der zurückgelegte Weg. Ist $f(x)$ ein Zufluss, dann ist $I_0(x)$ die gesammelte Menge.

Integralfunktionen starten immer bei null und "akkumulieren" dann die Werte von $f$ . Deshalb sind sie besonders nützlich bei Wachstums- und Sammelprozessen.

Denk dran: Die Integralfunktion ist wie ein Konto, auf das kontinuierlich eingezahlt (oder abgehoben) wird!

Wir dachten schon, du fragst nie...

Unser KI-Begleiter ist ein speziell für Schüler entwickeltes KI-Tool, das mehr als nur Antworten bietet. Basierend auf Millionen von Knowunity-Inhalten liefert er relevante Informationen, personalisierte Lernpläne, Quizze und Inhalte direkt im Chat und passt sich deinem individuellen Lernweg an.

Du kannst die App im Google Play Store und im Apple App Store herunterladen.

Genau! Genieße kostenlosen Zugang zu Lerninhalten, vernetze dich mit anderen Schülern und hol dir sofortige Hilfe – alles direkt auf deinem Handy.

Rekonstruktion von Beständen aus Änderungsraten

Stammfunktionen und der Hauptsatz

Integrale berechnen und verstehen

Integrationsregeln - Deine Rechenwerkzeuge

Integralfunktionen verstehen

Flächeninhalte richtig berechnen

Übungen und Stammfunktionen finden

Bestimmte Integrale berechnen

Anwendungen in Sachaufgaben

Integralfunktionen interpretieren

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Wo kann ich die Knowunity-App herunterladen?

Ist Knowunity wirklich kostenlos?

Ähnlicher Inhalt

Cálculo

Integrales

Técnicas de integración

A-Level Maths 2022 Solutions

Algebra und Analysis Grundlagen

Resumen de cada tema teniendo en cuenta la sgte información

Beliebtester Inhalt: Integral

Mathematik Abitur Themenübersicht

Analyse und Funktionen

Integralrechnung Grundlagen

Mathe Klausur Q1 nr.1

Integralrechnung Grundlagen

Flächeninhalte und Integrale

Mathe Abitur GK: Analysis

Integralrechnung Klausur Q1

Mathe Abi 25

Beliebtester Inhalt in Mathe

ZP10 Mathe Zusammenfassung NRW

Mathe ZP10 Zusammenfassung NRW

Mathematik Themenübersicht ZP 2024

Prüfungsvorbereitung MSA Klasse 10

Mathematik ZP10 Zusammenfassung

Alles was du für die ZP10 können musst! (VOLLSTÄNDIG) für Gymnasium und Realschule

Lernzettel ZP 10 Mathe

Mathematik Abitur Themenübersicht

Mathe Abi26 Zusammenfassung NRW

Beliebtester Inhalt

Der zerbrochene Krug

Der zerbrochene Krug von Heinrich von Kleist

Der zerbrochne Krug

Heimsuchung_JennyErpenbeck_Abitur

ZP10 Mathe Zusammenfassung NRW

Der zerbrochene Krug: Analyse

Englisch LK Abitur 2025

Schreibkompetenzen Deutsch LK

Jenny Erpenbeck "Heimsuchung"

Schüler lieben uns — und du auch.

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Rekonstruktion von Beständen aus Änderungsraten

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Stammfunktionen und der Hauptsatz

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Integrale berechnen und verstehen

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Integrationsregeln - Deine Rechenwerkzeuge

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Integralfunktionen verstehen

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Flächeninhalte richtig berechnen

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Übungen und Stammfunktionen finden

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Bestimmte Integrale berechnen

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Anwendungen in Sachaufgaben

Melde dich an, um den Inhalt zu sehen. Kostenlos!

Integralfunktionen interpretieren

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Wo kann ich die Knowunity-App herunterladen?

Ist Knowunity wirklich kostenlos?

Ähnlicher Inhalt

Cálculo

Integrales

Técnicas de integración