Mathematik

Logarithmische und Exponentialfunktionen

Exponentialfunktion

689

•

Aktualisiert Mar 22, 2026

•

7 Seiten

Funktionen leicht verständlich - Mathe Grundwissen Klasse 10

Dream

@dream_9za93

Mathematik kann echt überwältigend sein, aber diese Zusammenfassung bringt alle... Mehr anzeigen

1 / 7

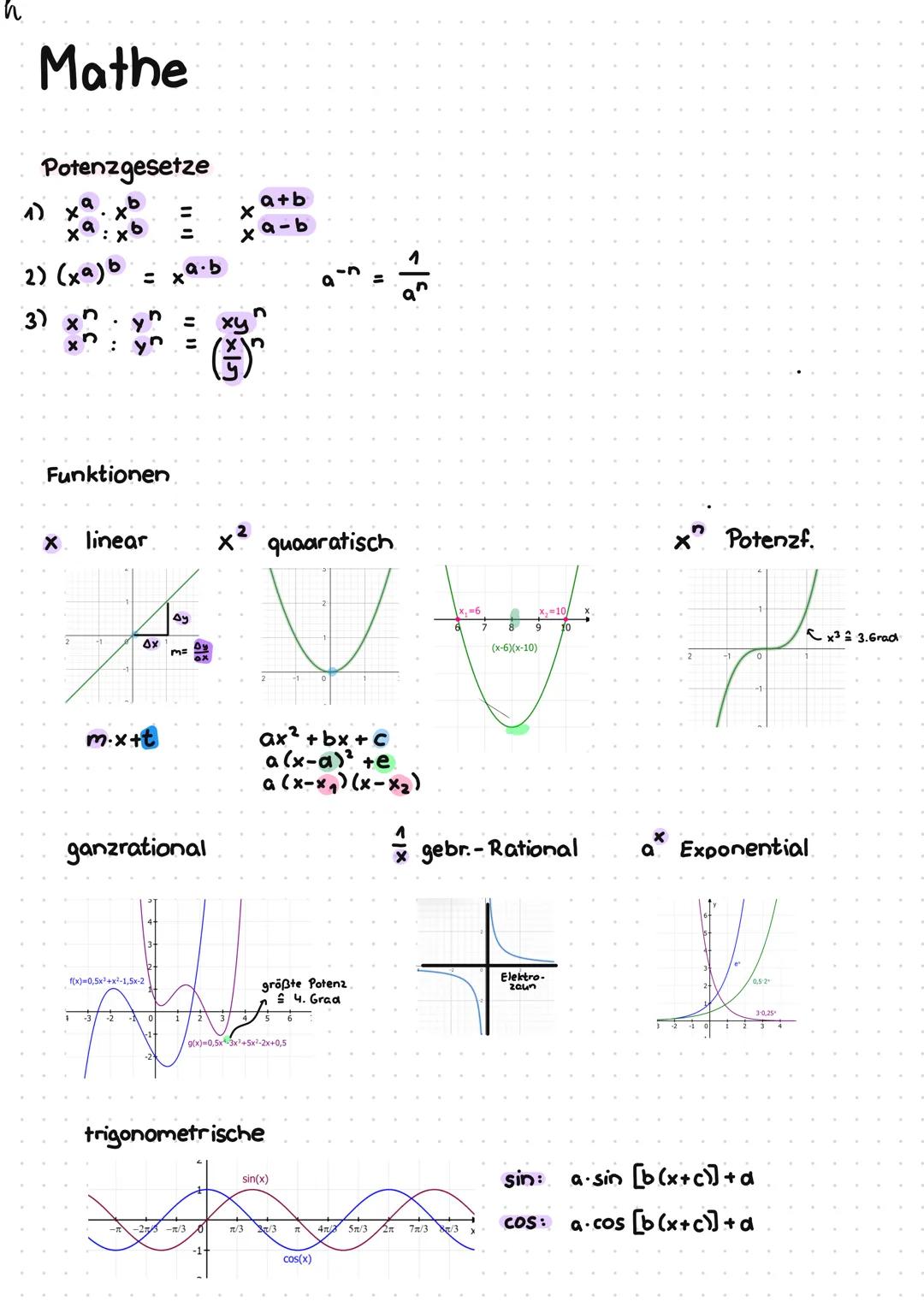
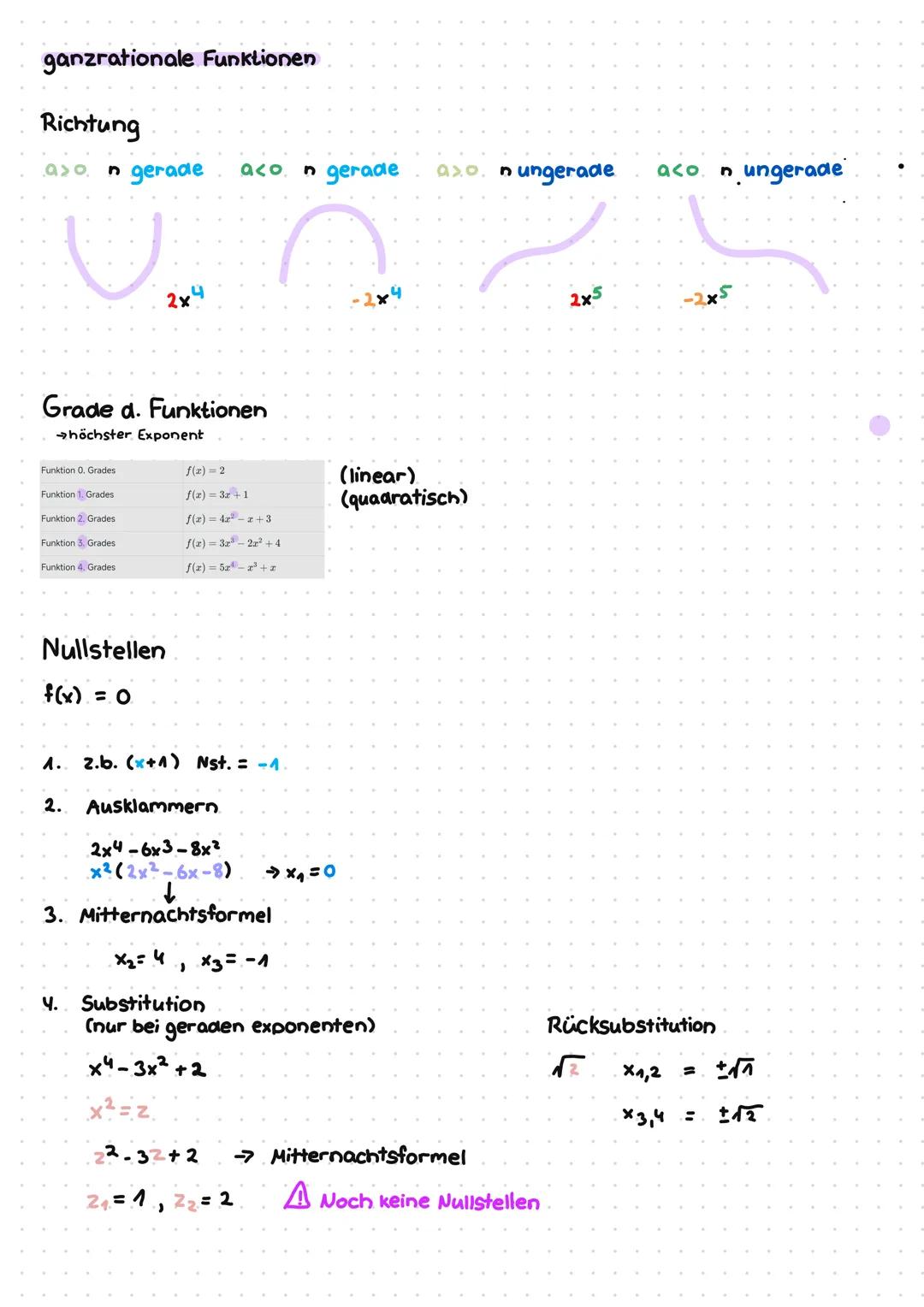
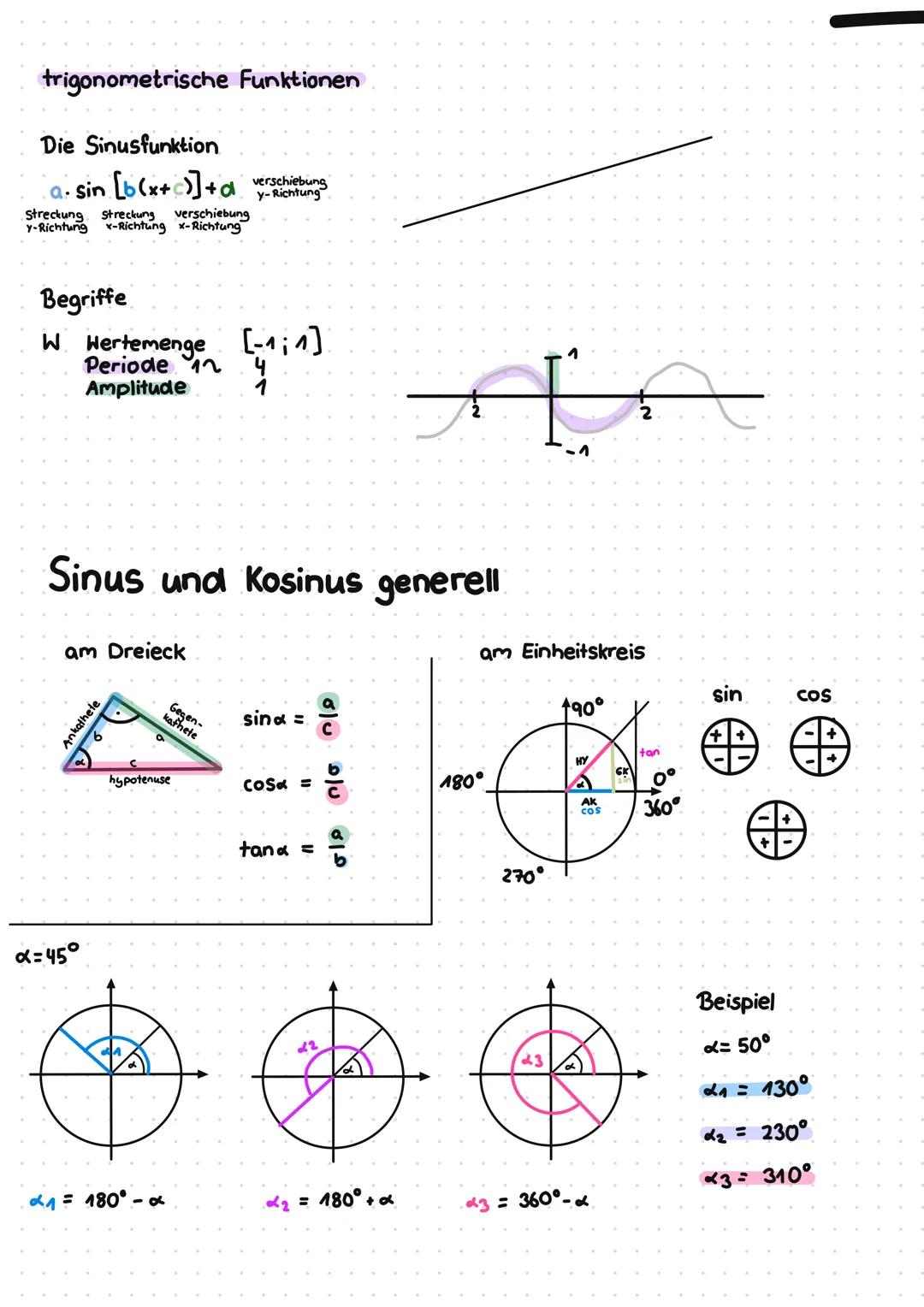
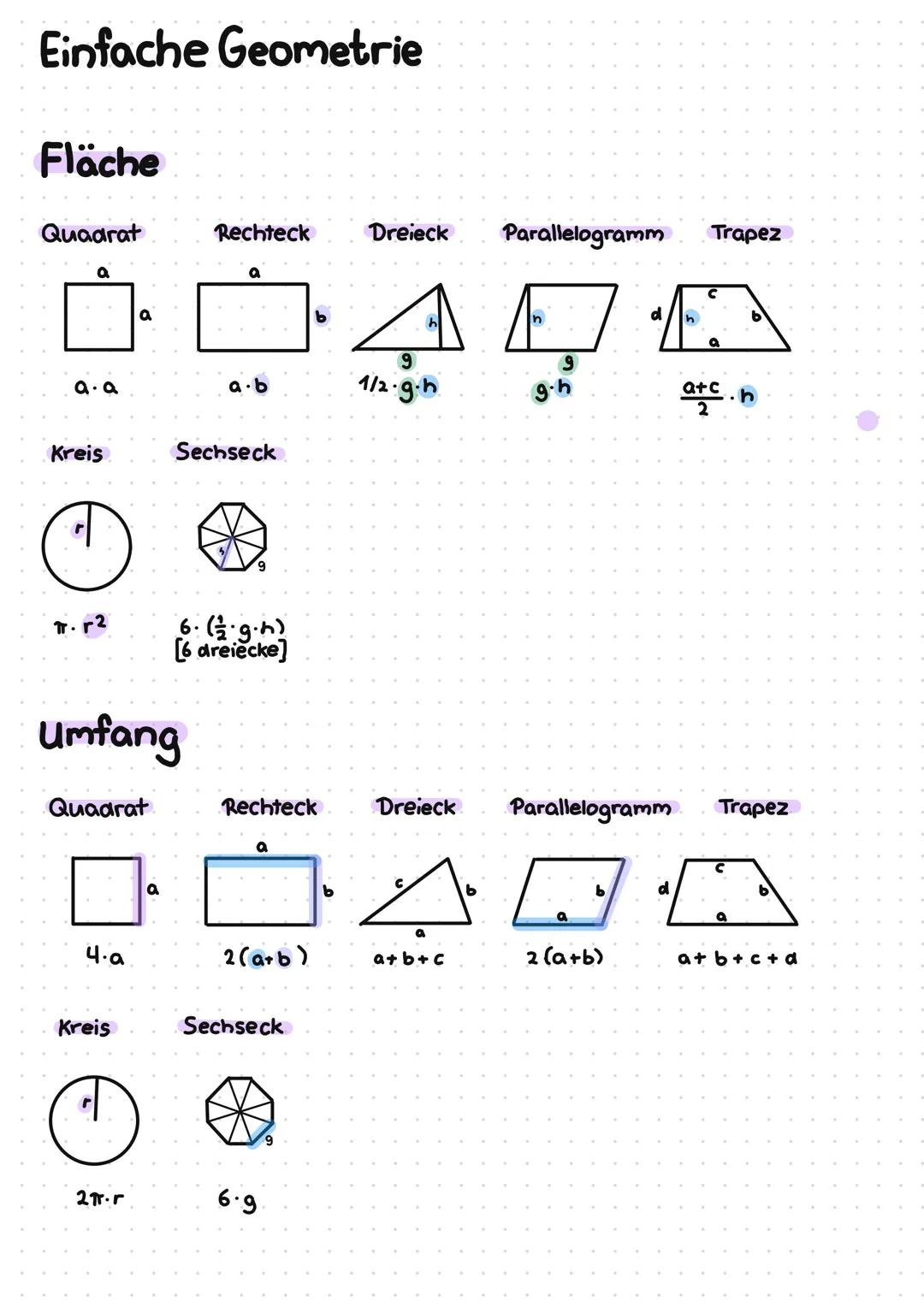
$h # Mathe Potenzgesetze 1) $x^a \cdot x^b = x^{a+b}$ $x^a : x^b = x^{a-b}$ 2) $(xa)^b = x^{a \cdot b}$ $a^{-n} = \frac{1}{a^n}$ 3) $$

Potenzgesetze und Funktionstypen

Potenzgesetze sind die Grundlage für fast alles in Mathe - und sie sind einfacher als du denkst! Das wichtigste Gesetz: $x^a \cdot x^b = x^{a+b}$ bedeutet einfach, dass du die Exponenten addierst. Bei der Division subtrahierst du sie: $x^a : x^b = x^{a-b}$ .

Die verschiedenen Funktionstypen haben alle ihre eigenen Charakteristika. Lineare Funktionen $m \cdot x + t$ ergeben immer eine gerade Linie, während quadratische Funktionen $$ax^2 + bx + c$$ die typischen Parabeln bilden.

Ganzrationale Funktionen erkennst du am höchsten Exponenten - das ist der Grad der Funktion. Eine Funktion wie $f(x) = 0,5x^4 + x^2 - 1,5x - 2$ ist also eine Funktion 4. Grades.

Merktipp: Bei Exponentialfunktionen $$a^x$$ steht die Variable im Exponenten, bei Potenzfunktionen $$x^n$$ in der Basis!

$h # Mathe Potenzgesetze 1) $x^a \cdot x^b = x^{a+b}$ $x^a : x^b = x^{a-b}$ 2) $(xa)^b = x^{a \cdot b}$ $a^{-n} = \frac{1}{a^n}$ 3) $$

Quadratische Funktionen meistern

Quadratische Funktionen kommen in drei verschiedenen Formen daher, die alle ihre Vorteile haben. Die Normalform $ax^2 + bx + c$ ist perfekt für Berechnungen, die Scheitelform $a(x-d)^2 + e$ zeigt dir sofort den Scheitelpunkt.

Die Nullstellenform $a(x-x_1)(x-x_2)$ funktioniert nur, wenn die Parabel die x-Achse schneidet. Mit der Mitternachtsformel $\frac{-b \pm \sqrt{b^2-4ac}}{2a}$ findest du immer die Nullstellen - falls welche existieren.

Das Umwandeln von Normal- in Scheitelform läuft über die quadratische Ergänzung. Du klammerst zuerst den Faktor vor $x^2$ aus, dann nimmst du die Hälfte der Zahl vor dem $x$ , quadrierst sie und addierst/subtrahierst sie gleichzeitig.

Praxis-Tipp: Für Klassenarbeiten solltest du alle drei Formen sicher beherrschen - sie machen verschiedene Aufgabentypen super einfach!

$h # Mathe Potenzgesetze 1) $x^a \cdot x^b = x^{a+b}$ $x^a : x^b = x^{a-b}$ 2) $(xa)^b = x^{a \cdot b}$ $a^{-n} = \frac{1}{a^n}$ 3) $$

Ganzrationale Funktionen und ihre Nullstellen

Das Verhalten ganzrationaler Funktionen hängt von zwei Faktoren ab: dem Vorzeichen von $a$ und ob der höchste Exponent gerade oder ungerade ist. Bei geradem Grad gehen beide Äste in dieselbe Richtung, bei ungeradem Grad in entgegengesetzte.

Nullstellen finden ist oft wie ein Puzzle lösen. Zuerst schaust du, ob du etwas ausklammern kannst - oft ist $x$ oder $x^2$ ein Faktor. Was übrig bleibt, löst du mit der Mitternachtsformel.

Die Substitution ist dein Geheimtrick bei Funktionen mit nur geraden Exponenten. Du ersetzt $x^2$ durch $z$ und machst aus $x^4 - 3x^2 + 2$ einfach $z^2 - 3z + 2$ . Nach dem Lösen musst du aber zurücksubstituieren - vergiss das nicht!

Wichtig: Bei der Rücksubstitution entstehen oft mehrere Nullstellen aus einer z-Lösung, weil $x = \pm\sqrt{z}$ !

$h # Mathe Potenzgesetze 1) $x^a \cdot x^b = x^{a+b}$ $x^a : x^b = x^{a-b}$ 2) $(xa)^b = x^{a \cdot b}$ $a^{-n} = \frac{1}{a^n}$ 3) $$

Exponentialfunktionen verstehen

Exponentialfunktionen $a \cdot b^x$ beschreiben Wachstum und Zerfall perfekt. Der Anfangswert $a$ ist der y-Achsenabschnitt, der Wachstumsfaktor $b$ bestimmt, wie schnell es wächst oder schrumpft.

Den Wachstumsfaktor berechnest du aus Prozentangaben: 20% Wachstum bedeutet $b = 1,20$ . Mit zwei Punkten stellst du ein Gleichungssystem auf und löst nach $a$ und $b$ auf.

Linear oder exponentiell unterscheiden ist einfach: Bei linearem Wachstum kommen pro Zeitschritt gleiche Beträge dazu, bei exponentiellem Wachstum wird immer mit demselben Faktor multipliziert.

Der Logarithmus ist das Gegenstück zur Exponentialfunktion. Wenn $2^x = 8 $, dann ist$ x = \log_2 8 = 3$. Das brauchst du, um nach dem Exponenten aufzulösen.

Eselsbrücke: $b > 1$ = steigend, $0 < b < 1$ = fallend. So einfach ist das!

$h # Mathe Potenzgesetze 1) $x^a \cdot x^b = x^{a+b}$ $x^a : x^b = x^{a-b}$ 2) $(xa)^b = x^{a \cdot b}$ $a^{-n} = \frac{1}{a^n}$ 3) $$

Trigonometrische Funktionen

Sinus und Kosinus sind am Einheitskreis am einfachsten zu verstehen. Die Sinusfunktion hat die Periode $2\pi$ und schwingt zwischen -1 und 1 - das ist ihre Amplitude.

Die allgemeine Form $a \cdot \sin[b(x+c)] + d$ sieht kompliziert aus, aber jeder Parameter hat eine klare Bedeutung: $a$ streckt vertikal, $b$ streckt horizontal, $c$ verschiebt horizontal und $d$ verschiebt vertikal.

Am rechtwinkligen Dreieck gilt: $\sin \alpha = \frac{\text{Gegenkathete}}{\text{Hypotenuse}}$ und $\cos \alpha = \frac{\text{Ankathete}}{\text{Hypotenuse}}$ . Das ist besonders bei praktischen Aufgaben wichtig.

Trick: Für jeden Winkel $\alpha$ gibt es drei weitere Winkel mit demselben Sinuswert: $180°-\alpha $,$ 180°+\alpha $und$ 360°-\alpha$!

$h # Mathe Potenzgesetze 1) $x^a \cdot x^b = x^{a+b}$ $x^a : x^b = x^{a-b}$ 2) $(xa)^b = x^{a \cdot b}$ $a^{-n} = \frac{1}{a^n}$ 3) $$

Geometrie-Formeln kompakt

Flächenberechnungen sind meist auswendig lernen, aber die Logik dahinter hilft. Parallelogramme und Rechtecke funktionieren nach dem Prinzip "Grundseite mal Höhe", Dreiecke sind die Hälfte davon.

Das Trapez ist der Mittelwert der parallelen Seiten mal Höhe: $\frac{a+c}{2} \cdot h$ . Beim Kreis ist die Fläche $\pi r^2$ - eine der wichtigsten Formeln überhaupt.

Umfänge sind logischer: Du addierst einfach alle Seitenlängen. Beim Kreis ist der Umfang $2\pi r$, beim Quadrat $4a$. Das Sechseck besteht aus sechs gleichen Seiten.

Praxis-Tipp: Zeichne dir die Figuren immer auf - so siehst du sofort, welche Formel du brauchst!

$h # Mathe Potenzgesetze 1) $x^a \cdot x^b = x^{a+b}$ $x^a : x^b = x^{a-b}$ 2) $(xa)^b = x^{a \cdot b}$ $a^{-n} = \frac{1}{a^n}$ 3) $$

Prozentrechnung einfach erklärt

Prozentrechnung ist eigentlich nur ein Dreisatz in Verkleidung. Du hast immer drei Größen: Grundwert (das Ganze), Prozentwert (das Ergebnis) und Prozentsatz (wieviel Prozent).

Die Grundformel $\frac{\text{Prozentwert}}{\text{Prozentsatz} \cdot \text{Grundwert}} \times 100%$ sieht kompliziert aus, aber das Prinzip ist einfach: "5% von 100 sind 5".

In praktischen Aufgaben erkennst du den Grundwert daran, dass er meist nach "von" steht. Der Prozentwert ist das konkrete Ergebnis, der Prozentsatz gibt an, welcher Anteil gemeint ist.

Merk-Hilfe: Prozent bedeutet "von hundert" - deshalb rechnest du immer mit dem Faktor 100!

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Unser KI-Begleiter ist ein speziell für Schüler entwickeltes KI-Tool, das mehr als nur Antworten bietet. Basierend auf Millionen von Knowunity-Inhalten liefert er relevante Informationen, personalisierte Lernpläne, Quizze und Inhalte direkt im Chat und passt sich deinem individuellen Lernweg an.

Wo kann ich die Knowunity-App herunterladen?

Du kannst die App im Google Play Store und im Apple App Store herunterladen.

Ist Knowunity wirklich kostenlos?

Genau! Genieße kostenlosen Zugang zu Lerninhalten, vernetze dich mit anderen Schülern und hol dir sofortige Hilfe – alles direkt auf deinem Handy.

Beliebtester Inhalt: Exponentialfunktion

Exponentielle Wachstumsmodelle

Entdecken Sie die Grundlagen der exponentiellen Wachstums- und Zerfallsfunktionen. Diese Zusammenfassung behandelt wichtige Konzepte wie logarithmische Umstellungen, lineares Wachstum, exponentielles Wachstum und Zerfall sowie deren mathematische Formeln. Ideal für Studierende, die sich auf Prüfungen vorbereiten oder ihr Verständnis von Wachstumsprozessen vertiefen möchten.

Funktionen leicht verständlich - Mathe Grundwissen Klasse 10

Potenzgesetze und Funktionstypen

Quadratische Funktionen meistern

Ganzrationale Funktionen und ihre Nullstellen

Exponentialfunktionen verstehen

Trigonometrische Funktionen

Geometrie-Formeln kompakt

Prozentrechnung einfach erklärt

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Wo kann ich die Knowunity-App herunterladen?

Ist Knowunity wirklich kostenlos?

Ähnlicher Inhalt

Quadratische Funktionen: Faktorisierte Form in Normalform umformen

Umkehrfunktion

Ganzrationale Funktionen Graphen zuordnen

Beliebtester Inhalt: Exponentialfunktion

Exponentielle Wachstumsmodelle

Exponentialfunktionen und Logarithmen

Exponentielles Wachstum: Klausurhilfe

Exponentialfunktionen verstehen

Exponentialfunktionen und Logarithmen

Graphen von Exponentialfunktionen

Exponential- und Lineares Wachstum

Exponentialfunktionen verstehen

Exponentialwachstum verstehen

Beliebtester Inhalt in Mathe

Kombinatorik und Wahrscheinlichkeiten

Mathe Abi: Analysis, Vektoren, Stochastik

Mathematik Abitur Zusammenfassung

Analysis: Funktionsscharen & Ableitungen

Mathe-Abitur 2024: Stochastik & Vektoren

Integralrechnung Grundlagen

Integralrechnung und Flächenberechnung

Mathe GK Abi

Mathe Abi26 Zusammenfassung NRW

Beliebtester Inhalt

Abilernzettel Heimsuchung 2025

Der zerbrochene Krug

Der zerbrochene Krug: Analyse

Heimsuchung - Jenny Erpenbeck

Zusammenfassung Heimsuchung

Heimsuchung - Jenny Erpenbeck - KompletteZusammenfassung jedemKapitel+Analyse+Merkmale+Klausur Übung

Der zerbrochene Krug von Heinrich von Kleist

Charaktere aus Heimsuchung von Jenny Erpenbeck

Inhaltsverzeichnis Heimsuchung Jenny Erpenbeck

Findest du nicht, was du suchst? Entdecke andere Fächer.

Schüler lieben uns — und du auch.

4.6/5

4.7/5

Funktionen leicht verständlich - Mathe Grundwissen Klasse 10

Melde dich an, um den Inhalt zu sehenKostenlos!

Potenzgesetze und Funktionstypen

Melde dich an, um den Inhalt zu sehenKostenlos!

Quadratische Funktionen meistern

Melde dich an, um den Inhalt zu sehenKostenlos!

Ganzrationale Funktionen und ihre Nullstellen

Melde dich an, um den Inhalt zu sehenKostenlos!

Exponentialfunktionen verstehen

Melde dich an, um den Inhalt zu sehenKostenlos!

Trigonometrische Funktionen

Melde dich an, um den Inhalt zu sehenKostenlos!

Geometrie-Formeln kompakt

Melde dich an, um den Inhalt zu sehenKostenlos!

Prozentrechnung einfach erklärt

Wir dachten schon, du fragst nie...

Was ist der Knowunity KI-Begleiter?

Wo kann ich die Knowunity-App herunterladen?

Ist Knowunity wirklich kostenlos?

Ähnlicher Inhalt

Quadratische Funktionen Umformen

Umkehrfunktionen verstehen

Graphen ganzrationaler Funktionen

Nullstellen quadratischer Funktionen

Funktionen und Gleichungssysteme

Symmetrie und Potenzfunktionen

Ähnlicher Inhalt

Quadratische Funktionen: Faktorisierte Form in Normalform umformen

Umkehrfunktion

Ganzrationale Funktionen Graphen zuordnen