Änderungsraten - Der Einstieg in die Analysis

Stell dir vor, du fährst Auto und willst wissen, wie schnell du warst. Mittlere Änderungsraten geben dir die Durchschnittsgeschwindigkeit über eine bestimmte Strecke an. Mathematisch entspricht das der Sekantensteigung zwischen zwei Punkten auf dem Funktionsgraphen.

Die Formel dafür ist der Differenzenquotient: m = $f(b) - f(a)$/$b - a$. Das ist einfach "Änderung in y geteilt durch Änderung in x" - genau wie bei normalen Geradensteigungen.

Momentane Änderungsraten sind viel spannender: Sie zeigen dir die exakte Geschwindigkeit in einem bestimmten Moment - wie der Tacho in deinem Auto. Hier wird das Intervall immer kleiner, bis aus der Sekante eine Tangente wird.

Merke dir: Die momentane Änderungsrate ist der Grenzwert der mittleren Änderungsrate und führt direkt zur Ableitung!

Grenzwerte und die h-Methode

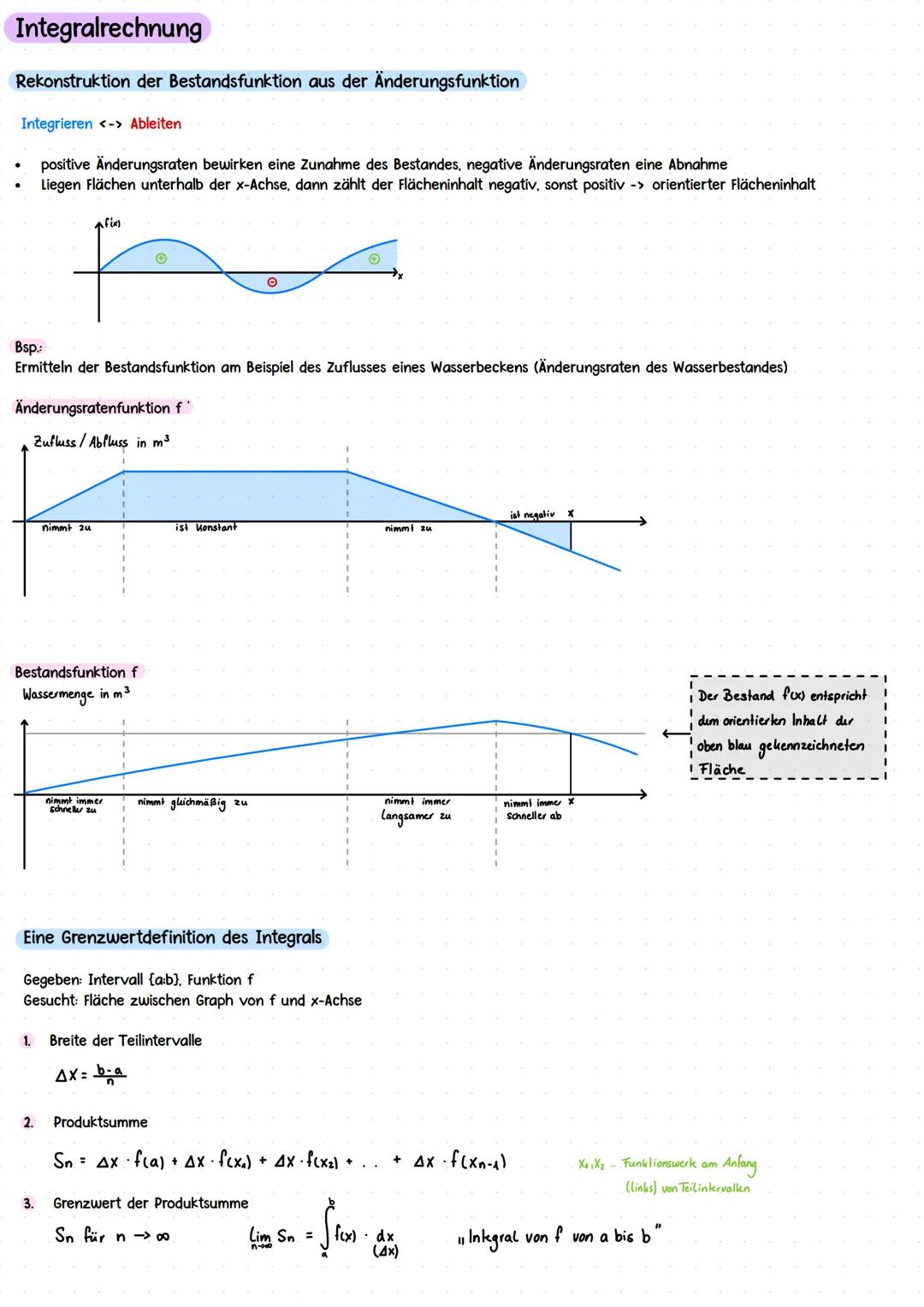
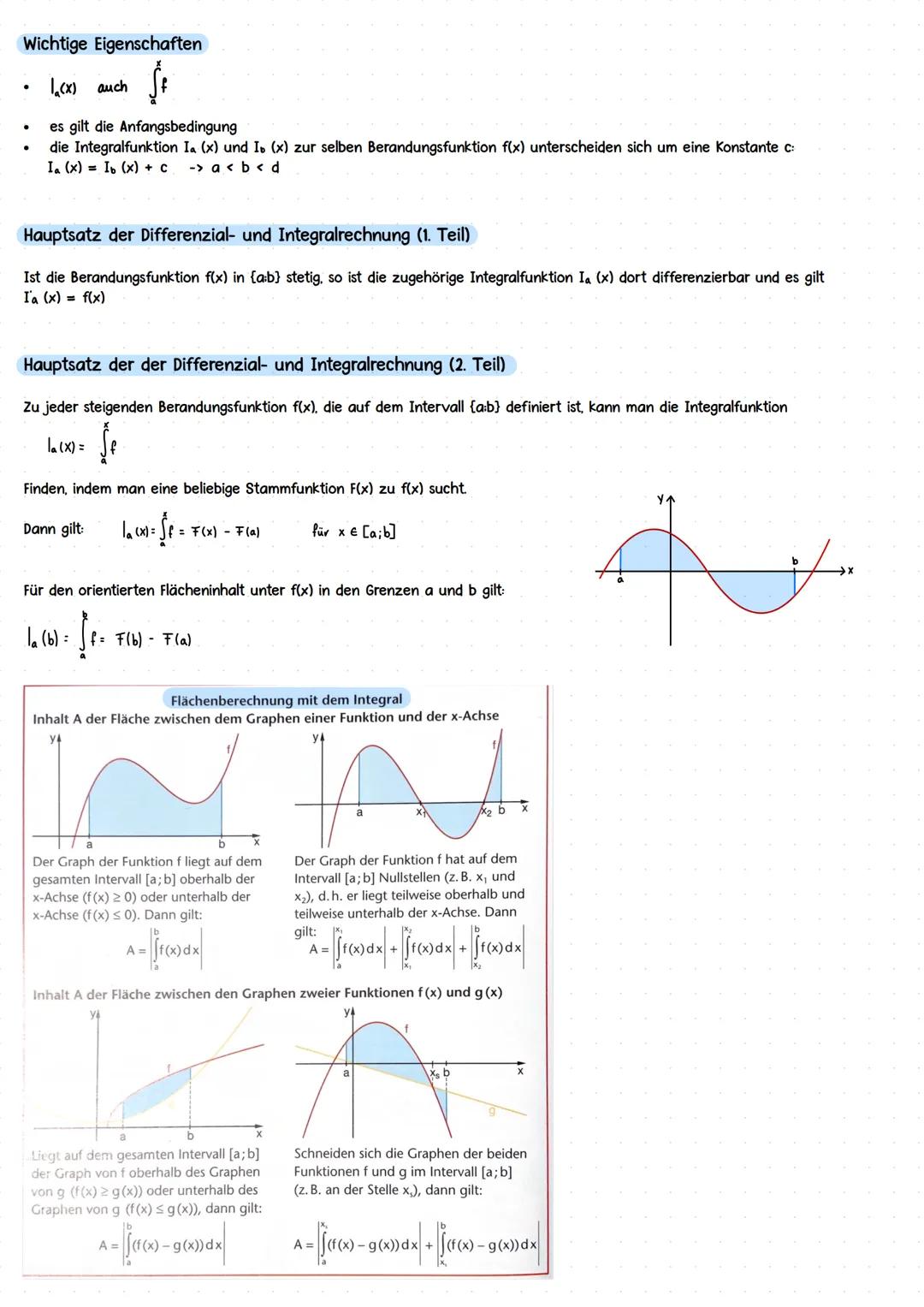
Grenzwerte zeigen dir, wie sich Funktionen im Unendlichen verhalten. Mit lim schreibst du auf, was passiert, wenn x gegen +∞ oder -∞ geht. Bei f(x) = x² geht's immer gegen +∞, egal aus welcher Richtung.

Bei e-Funktionen ist's interessanter: e^x geht gegen +∞ für x→+∞, aber gegen 0 für x→-∞. Das liegt an der besonderen Form der e-Funktion.

Die Sekantensteigungsfunktion ist ein cleverer Trick: Sie ordnet jedem x-Wert die Steigung der Sekante zu. Mit einem kleinen h-Wert bekommst du schon eine super Näherung für die echte Ableitung.

Die h-Methode ist der mathematisch saubere Weg zur Ableitung: f'(x) = lim(h→0) $f(x+h) - f(x)$/h. Damit kannst du jede Ableitung herleiten, auch wenn's manchmal etwas Rechenarbeit bedeutet.

Tipp: Die h-Methode verstehen ist Gold wert für das Verständnis von Ableitungen!

Ableitungen - Die Werkzeugkiste der Analysis

Beim graphischen Ableiten merkst du dir einfache Regeln: Extrempunkte von f werden zu Nullstellen von f', Wendepunkte von f werden zu Extrempunkten von f'. Positive Steigung bedeutet f' oberhalb der x-Achse.

Die Ableitungsregeln sind dein Handwerkszeug. Potenzregel: x^n wird zu n·x^$n-1$. Faktor- und Summenregel sind selbsterklärend - Konstanten bleiben, Summen werden einzeln abgeleitet.

Produktregel brauchst du bei f(x) = g(x)·h(x): f'(x) = g'(x)·h(x) + g(x)·h'(x). Die Kettenregel bei verschachtelten Funktionen: äußere Ableitung mal innere Ableitung.

Die Quotientenregel ist etwas sperriger: $h(x)·g'(x) - g(x)·h'(x)$ / $h(x)$². Für trigonometrische Funktionen merkst du dir den Kreis: sin→cos→-sin→-cos.

Praxistipp: Lerne die Grundregeln auswendig - sie sparen dir später enorm viel Zeit!

Tangenten und Krümmungsverhalten

Tangentengleichungen folgen dem Schema y = f'(a)·$x-a$ + f(a). Die Steigung ist f'(a), den y-Achsenabschnitt berechnest du durch Einsetzen.

Die zweite Ableitung f''(x) verrät dir das Krümmungsverhalten. Bei f''(x) > 0 ist der Graph linksgekrümmt (wie ein Lächeln), bei f''(x) < 0 rechtsgekrümmt (wie ein Frown). Wendepunkte liegen da, wo f''(x) = 0 und das Vorzeichen wechselt.

Beim Globalverlauf von Polynomen kommt's auf den höchsten Exponenten an. Ist n gerade, gehen beide Äste in dieselbe Richtung. Ist n ungerade, gehen sie in entgegengesetzte Richtungen. Das Vorzeichen des Leitkoeffizienten bestimmt, ob's nach oben oder unten geht.

Eselsbrücke: Linksgekrümmt = Lächeln = f'' positiv!

Funktionsanalyse komplett

Das Vorzeichen von f'(x) verrät dir alles über Steigen und Fallen: f'(x) > 0 bedeutet streng monoton steigend, f'(x) < 0 bedeutet fallend. Vorzeichenwechsel von f'(x) markieren Extrempunkte: von + zu - gibt's einen Hochpunkt, von - zu + einen Tiefpunkt.

Bei f''(x) geht's ums Krümmungsverhalten: f''(x) > 0 heißt linksgekrümmt, f''(x) < 0 heißt rechtsgekrümmt. Vorzeichenwechsel von f''(x) markieren Wendepunkte.

Symmetrien erkennst du an den Exponenten: Nur ungerade Exponenten → Punktsymmetrie zum Ursprung $f(-x) = -f(x)$. Nur gerade Exponenten → Achsensymmetrie zur y-Achse $f(-x) = f(x)$.

Merkhilfe: f' für Extrema, f'' für Wendepunkte - nie verwechseln!

Optimierung - Mathe trifft Realität

Optimierungsprobleme löst du systematisch in vier Schritten. Erstens: Skizze anfertigen und Zielfunktion aufstellen (meist Fläche, Volumen oder Kosten). Zweitens: Nebenbedingungen aus geometrischen oder anderen Zusammenhängen finden.

Drittens: Extremwert der Zielfunktion bestimmen - durch Ableitung und Nullsetzen oder über Wertetabellen. Viertens: Ergebnis interpretieren und auf Plausibilität prüfen.

Das Kegel-Beispiel zeigt's: Bei vorgegebener Mantellinie s ist das Volumen maximal, wenn das Verhältnis von Radius zu Höhe √2 beträgt. Das gilt für jede Mantellänge!

Der Trick ist meist, eine Variable durch die Nebenbedingung zu eliminieren, sodass du eine Funktion mit nur einer Variablen bekommst.

Erfolgsgeheimnis: Gute Skizze = halbe Lösung bei Optimierungsproblemen!

Steckbriefaufgaben - Funktionen rückwärts konstruieren

Steckbriefaufgaben sind wie Detektivarbeit: Du bekommst Hinweise und musst die unbekannte Funktion finden. Das Schema ist immer gleich: Allgemeine Funktionsgleichung + Ableitungen aufstellen, dann Informationen in ein Gleichungssystem übersetzen.

"Berührt die x-Achse" bedeutet f(x) = 0 UND f'(x) = 0. "Geht durch Punkt P" heißt einfach f(x) = y-Wert. "Tangente parallel zu Gerade" bedeutet gleiche Steigung.

Im Beispiel führten die Bedingungen zu einem 4×4-Gleichungssystem. Systematisches Einsetzen und Auflösen bringt dich zum Ziel.

Wichtige Begriffe: "Berührt" = Nullstelle + waagerechte Tangente, "schneidet" = nur Nullstelle, "Wendepunkt" = f''(x) = 0.

Strategie: Erst alle Bedingungen sammeln, dann systematisch das Gleichungssystem aufstellen!

Integralrechnung - Von der Änderung zum Bestand

Integrieren ist das Gegenteil von Ableiten. Du rekonstruierst aus der Änderungsrate den ursprünglichen Bestand. Positive Änderungsraten bedeuten Zunahme, negative Abnahme.

Das bestimmte Integral ∫$a bis b$ f(x) dx gibt den orientierten Flächeninhalt zwischen Funktionsgraph und x-Achse an. "Orientiert" heißt: Flächen unter der x-Achse zählen negativ.

Die Grenzwertdefinition teilt das Intervall in n kleine Stücke der Breite Δx = $b-a$/n auf. Die Summe aller Rechteckflächen wird für n→∞ zum exakten Integral.

Praktisch berechnest du Integrale aber nicht über Grenzwerte, sondern über Stammfunktionen - das kommt auf den nächsten Seiten.

Kernidee: Integral = Fläche unter der Kurve (mit Vorzeichen!)

Der Hauptsatz und Flächenberechnung

Der Hauptsatz der Analysis verbindet Ableitung und Integral: Ist F(x) eine Stammfunktion von f(x), dann ist ∫$a bis b$ f(x) dx = F(b) - F(a). Das macht Integralberechnung super effizient!

Integralfunktionen I_a(x) geben den Flächeninhalt von a bis x an. Verschiedene untere Grenzen unterscheiden sich nur um eine Konstante.

Bei der Flächenberechnung musst du auf Nullstellen achten. Liegt die Funktion komplett über oder unter der x-Achse, einfach integrieren und Betrag nehmen. Bei Nullstellen im Intervall musst du die Flächen getrennt berechnen und addieren.

Flächen zwischen zwei Funktionen berechnest du über ∫$a bis b$ |f(x) - g(x)| dx. Auch hier: Bei Schnittpunkten getrennt integrieren!

Praxistipp: Immer zuerst Nullstellen und Schnittpunkte finden, dann integrieren!

Integration in der Praxis

Die Integrationsregeln sind simple: Summenregel $Summe von Integralen = Integral der Summe$, konstante Faktoren vor das Integral ziehen, Vorzeichen ausklammern.

Rotationsvolumen berechnest du mit V = π ∫$a bis b$ $f(x)$² dx für Rotation um die x-Achse. Bei Rotation um die y-Achse brauchst du die Umkehrfunktion: y nach x auflösen, dann x und y vertauschen.

Uneigentliche Integrale gehen bis unendlich. Du ersetzt ∞ durch eine Variable (z.B. b) und bildest den Grenzwert: lim(b→∞) ∫$a bis b$ f(x) dx.

Das Beispiel ∫$0 bis ∞$ e^$-x$ dx = 1 zeigt: Manche Flächen bis unendlich haben trotzdem endlichen Inhalt!

Wow-Moment: Unendliche Flächen können endlichen Inhalt haben - Analysis ist magisch!