Abitur Mathe 2024

Das ist dein kompletter Guide für den Mathe-Leistungskurs im Abitur 2024. Diese Zusammenfassung deckt alle prüfungsrelevanten Themen ab, die du für eine erfolgreiche Abiturprüfung brauchst.

Die folgenden Seiten behandeln systematisch alle wichtigen Bereiche: Wahrscheinlichkeitsrechnung mit Binomial- und Normalverteilung, Vektorrechnung mit Geraden und Ebenen sowie Analysis mit Ableitungen und Integralen.

Tipp: Nutze diese Zusammenfassung als Nachschlagewerk und zur gezielten Wiederholung vor der Prüfung!

Binomialverteilung

Bernoulli-Experimente sind Zufallsexperimente mit genau zwei möglichen Ausgängen: Erfolg oder Misserfolg. Ein klassisches Beispiel ist sechsmaliges Würfeln, wobei die "6" als Erfolg zählt.

Die Bernoulli-Formel lautet: P$X=k$ = C(n,k) · p^k · q^$n-k$, wobei n die Anzahl der Durchführungen, k die Anzahl der Erfolge, p die Erfolgswahrscheinlichkeit und q = 1-p die Misserfolgswahrscheinlichkeit ist.

Bei Mindestens-Aufgaben arbeitest du oft mit der Gegenwahrscheinlichkeit. Beispiel Farbblindheit: "Mindestens einer ist farbenblind" bedeutet P(X≥1) = 1 - P$X=0$. Den Binomialkoeffizienten berechnest du mit C(n,k) = n!/$k!·(n-k)!$ oder vereinfacht durch Kürzen der Faktoren.

Merke: Bei CAS-Rechnern verwendest du nCr(n,k) für Binomialkoeffizienten und die Binomial-Funktion für Wahrscheinlichkeiten.

Normalverteilung

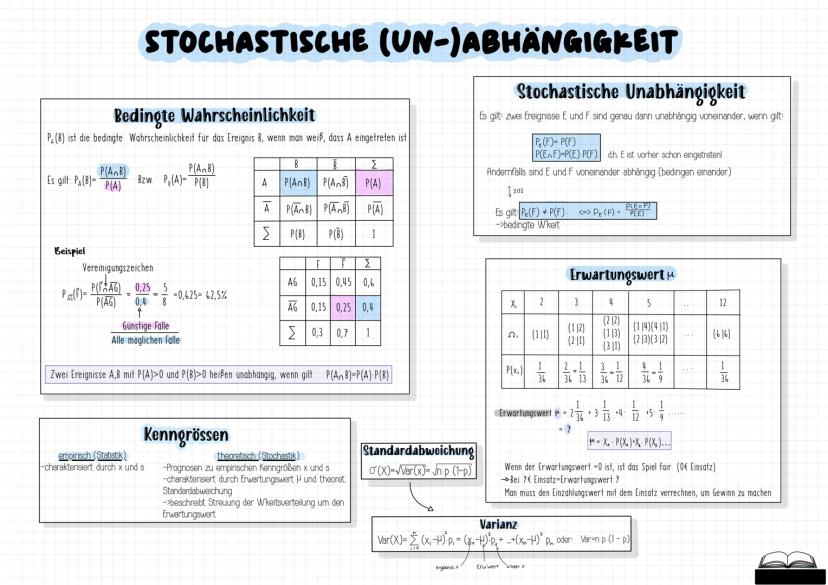
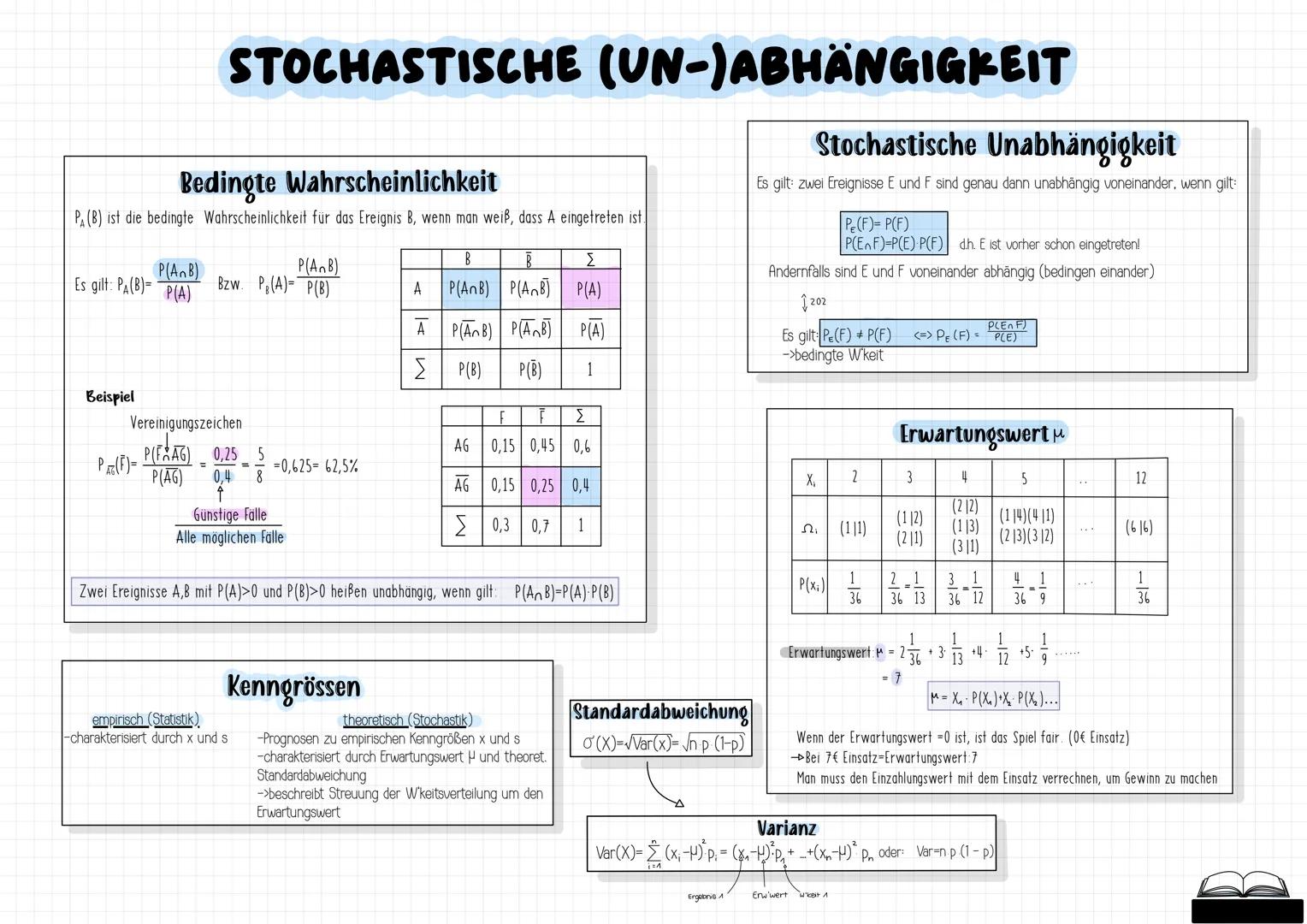
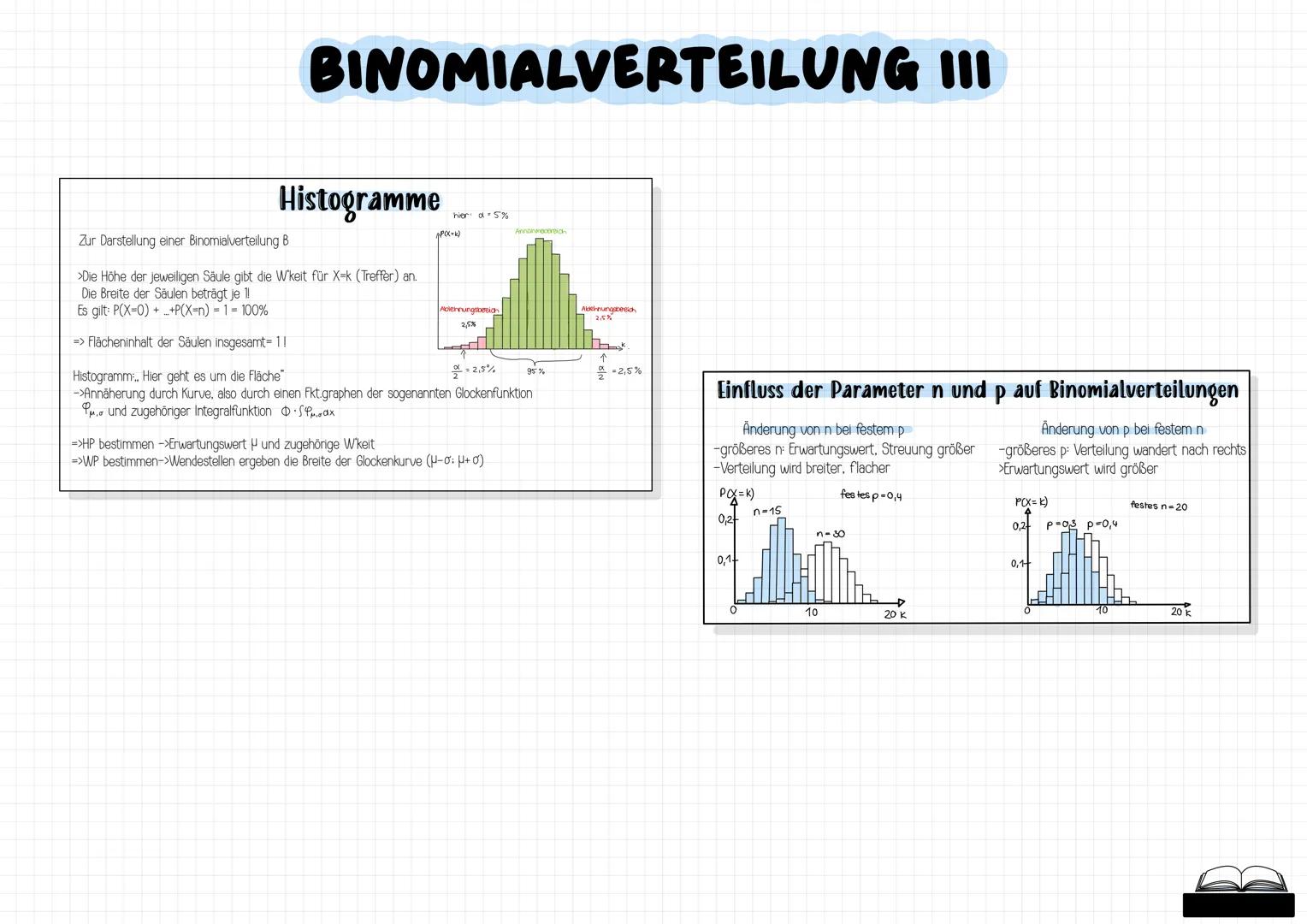
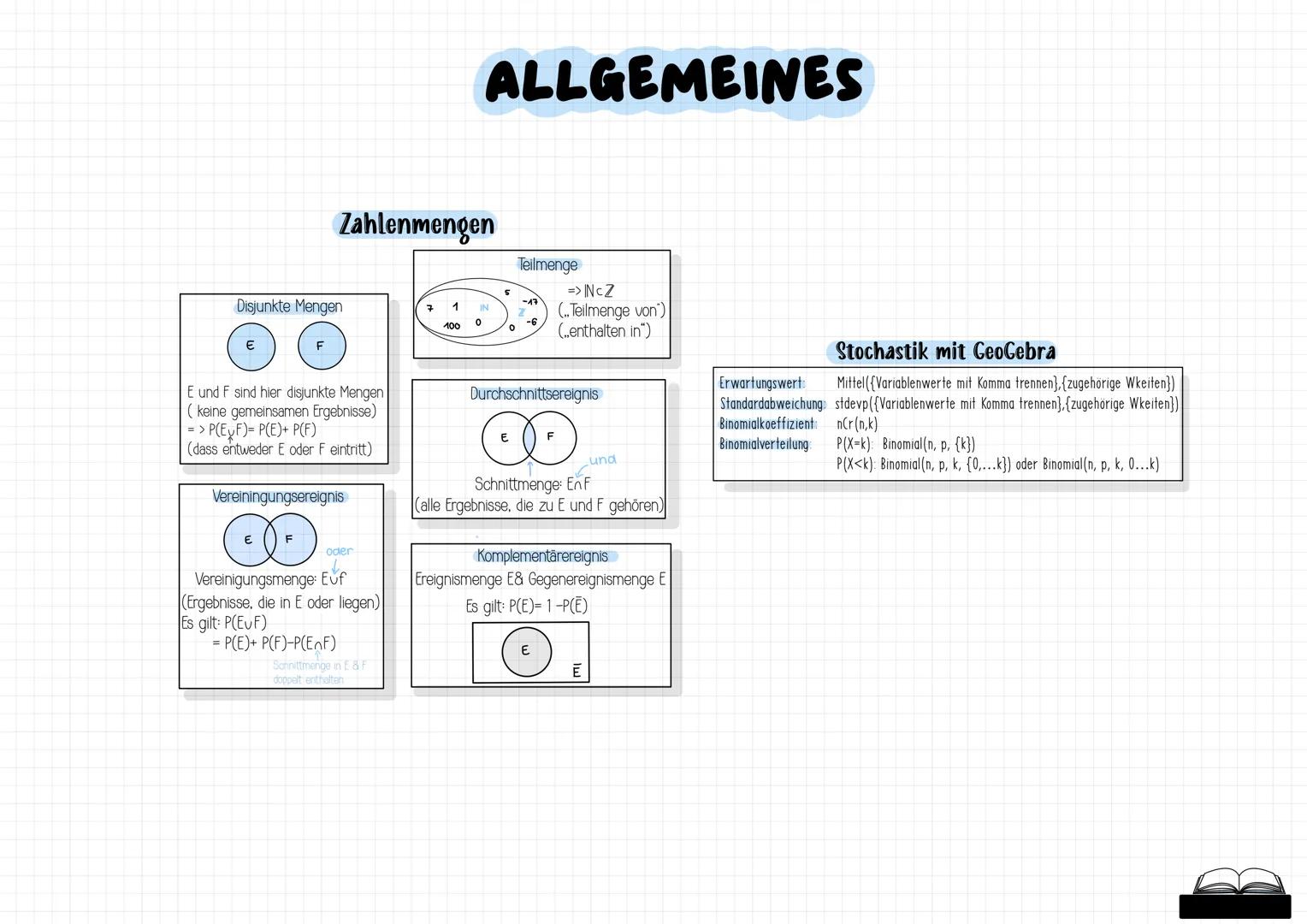
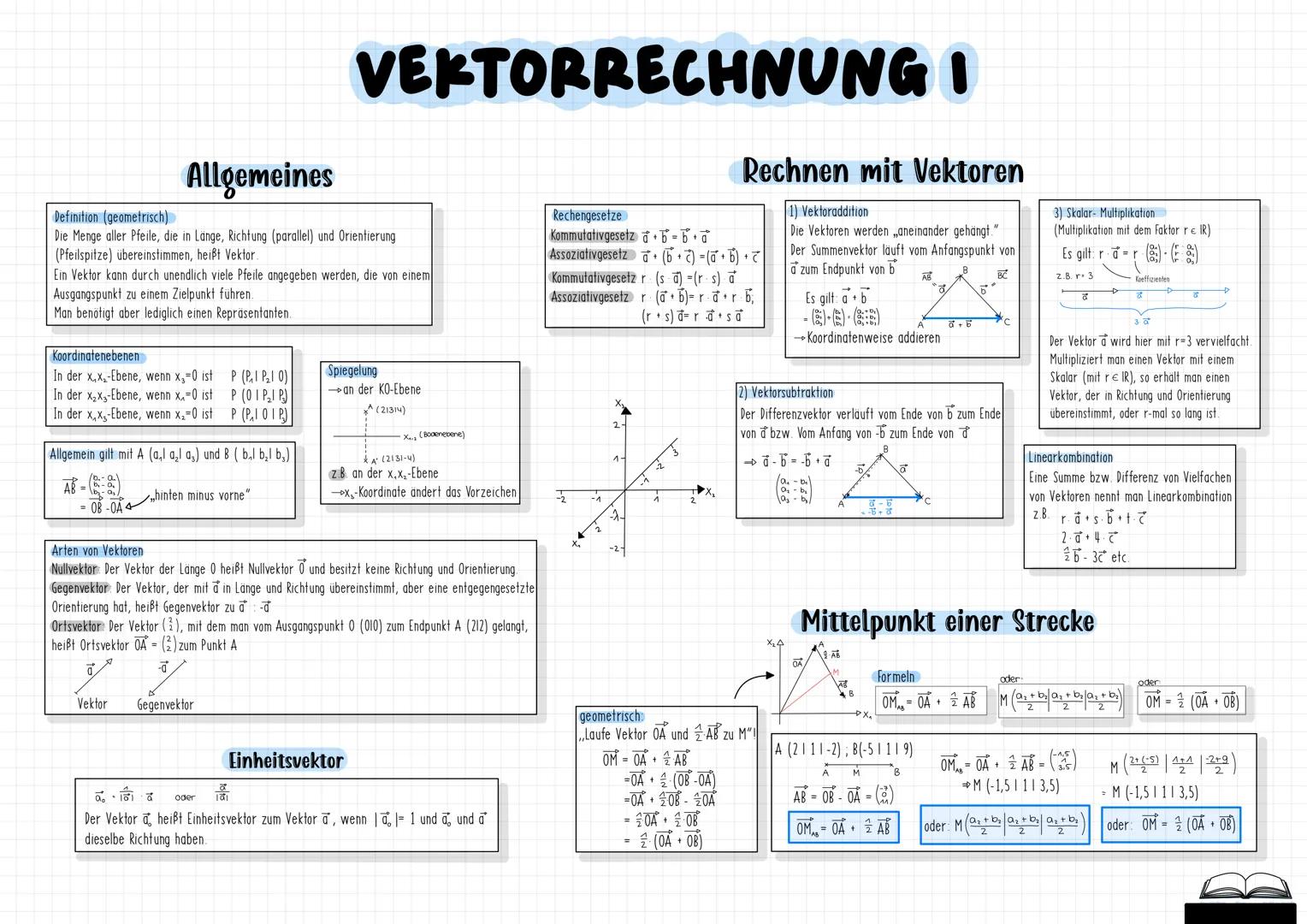
Die Gauß'sche Glockenfunktion ist symmetrisch zur y-Achse und hat ihr Maximum beim Erwartungswert μ. Die Wendestellen liegen bei μ±σ, wobei σ die Standardabweichung ist.

Im Vergleich zur Binomialverteilung ist die Normalverteilung stetig (kann alle reellen Werte annehmen) und hat keine Einzelwahrscheinlichkeiten - nur Intervallwahrscheinlichkeiten. Der Erwartungswert entspricht dem x-Wert des Hochpunkts.

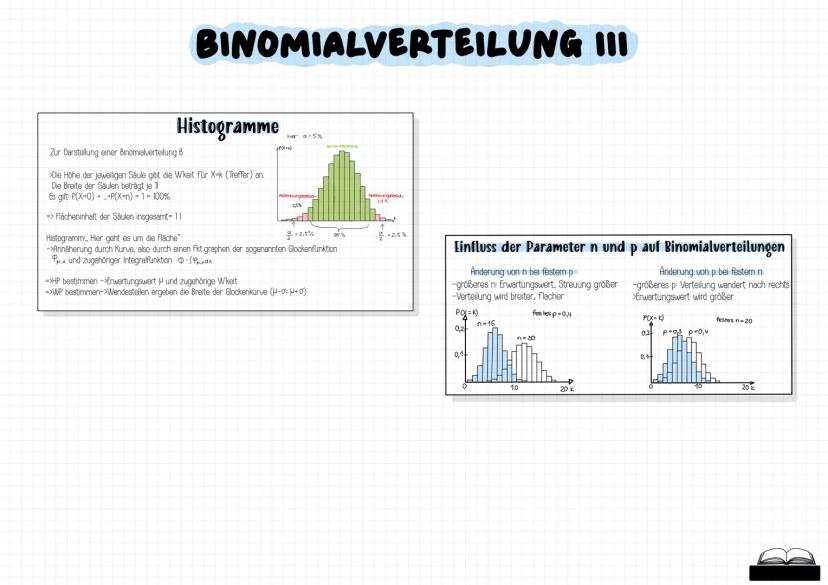
Der Satz von Moivre-Laplace besagt, dass Binomialverteilungen bei großen n durch Normalverteilungen angenähert werden können. Dabei verwendest du die Stetigkeitskorrektur: Das Integrationsintervall wird um ±0,5 erweitert.

Die Parameter μ und σ beeinflussen die Verteilung unterschiedlich: μ verschiebt die Kurve horizontal, während σ die Form bestimmt $kleiner σ = steiler, größer σ = flacher$.

CAS-Befehle: Normal(μ,σ,x) für Wahrscheinlichkeiten und InversNormal(μ,σ,p) für Quantile.

Vektorrechnung - Grundlagen

Das Kreuzprodukt (Vektorprodukt) berechnest du, indem du beide Vektoren zweimal untereinander schreibst, die obersten und untersten Zahlen streichst und über Kreuz multiplizierst. Es ergibt einen Vektor, der senkrecht zu beiden ursprünglichen Vektoren steht.

Ebenenformen gibt es in vier Varianten: Parameterform mit Stütz- und Spannvektoren, Normalengleichung, Koordinatengleichung und Hesse'sche Normalenform. Den Normalenvektor erhältst du durch das Kreuzprodukt der Richtungsvektoren.

Anwendungen des Vektorprodukts sind vielfältig: Flächeninhalt eines Parallelogramms |a⃗×b⃗|, eines Dreiecks ½|AB⃗×AC⃗| und Volumen eines Spats |(a⃗×b⃗)·c⃗|.

Vektoren sind kollinear (parallel), wenn sie Vielfache voneinander sind: u⃗ = r·v⃗. Drei Vektoren sind komplanar, wenn sie in einer Ebene liegen und linear abhängig sind.

Wichtig: Das Kreuzprodukt funktioniert nur im dreidimensionalen Raum und ist nicht kommutativ!

Lagebeziehungen

Gerade-Ebene-Beziehungen untersuchst du systematisch: Erst prüfst du auf Parallelität (Richtungsvektor senkrecht zum Normalenvektor), dann setzt du die Gerade in die Ebene ein und löst das entstehende Gleichungssystem.

Mögliche Lagen sind: Gerade durchstößt Ebene (eindeutige Lösung), Gerade liegt in Ebene (unendlich viele Lösungen) oder Gerade ist parallel zur Ebene (keine Lösung).

Ebene-Ebene-Beziehungen erkennst du an den Normalenvektoren: Sind sie Vielfache voneinander, sind die Ebenen parallel oder identisch. Ansonsten schneiden sie sich in einer Geraden.

Schnittwinkel berechnest du mit der Formel cos(α) = |a⃗·b⃗|/(|a⃗|·|b⃗|). Bei Geraden und Ebenen verwendest du die Beträge der Skalarprodukte. Für Gerade-Ebene-Winkel nimmst du den Sinus statt Kosinus.

Merke: Winkel zwischen Geraden und Ebenen liegen zwischen 0° und 90°, deshalb verwendest du Betragsstriche!

Abstände

Den Abstand Punkt-Gerade berechnest du über drei Methoden: Allgemeinen Punkt aufstellen und Minimum der Abstandsfunktion finden, Lotfußpunkt bestimmen oder die Formel d = |u⃗×PR⃗|/|u⃗| verwenden.

Für windschiefe Geraden stellst du allgemeine Punkte auf beiden Geraden auf, bildest einen Verbindungsvektor und löst das System mit den Bedingungen, dass dieser Vektor senkrecht zu beiden Richtungsvektoren steht.

Den Abstand Punkt-Ebene berechnest du am einfachsten mit der Hesse'schen Normalenform: d = |ax₁+bx₂+cx₃-d|/|n⃗|. Du setzt einfach die Koordinaten des Punktes ein und teilst durch die Länge des Normalenvektors.

Bei der Abstandsberechnung hilft oft die geometrische Interpretation: Der kürzeste Abstand ist immer die senkrechte Verbindung zwischen den Objekten.

Tipp: Die Hesse-Form ist meist der schnellste Weg für Punkt-Ebene-Abstände - lerne diese Formel auswendig!

Bewegungsaufgaben mit Vektoren

Bewegungsaufgaben löst du systematisch: Stelle Geradengleichungen für beide bewegten Objekte auf, berücksichtige dabei Geschwindigkeiten und Richtungen, und berechne dann die Distanzfunktion d(t).

Bei gegebener Geschwindigkeit bildest du zuerst den Einheitsvektor der Richtung und multiplizierst ihn mit der Geschwindigkeit. So erhältst du den Geschwindigkeitsvektor für die Geradengleichung.

Die Distanzfunktion d(t) = |P⃗ₜ - Q⃗ₜ| gibt den Abstand zu jedem Zeitpunkt an. Für den minimalen Abstand bildest du die Ableitung d'(t) und setzt sie gleich null.

Spiegelungen funktionieren über Vektoren: Bei Punktspiegelung an Z gilt OP⃗' = OZ⃗ + PZ⃗. Das Spiegelzentrum liegt genau in der Mitte zwischen Punkt und Bildpunkt.

Praxis-Tipp: Prüfe immer die Einheiten! Geschwindigkeit in km/h, Zeit in Stunden, dann stimmen auch die Abstände in km.

Ableitungen und Funktionenscharen

Die Tangentensteigung ist die momentane Änderungsrate und entspricht der ersten Ableitung f'(x) an der Stelle x. Für die Tangentengleichung y = mx + b berechnest du die Steigung durch Ableiten und den y-Achsenabschnitt durch Einsetzen.

Funktionenscharen enthalten einen Parameter a neben der Variablen x. Jeder Wert von a ergibt eine eigene Funktion der Schar. Du untersuchst sie wie normale Funktionen, aber behältst den Parameter bei.

Für knickfreie Übergänge zweier Funktionen müssen sie im Übergangspunkt denselben Funktionswert und dieselbe Steigung haben: f(x₀) = g(x₀) und f'(x₀) = g'(x₀).

Ruckfreie Übergänge erfordern zusätzlich gleiches Krümmungsverhalten: f''(x₀) = g''(x₀). Ortskurven entstehen, wenn du charakteristische Punkte (wie Extremstellen) für verschiedene Parameterwerte verbindest.

Strategietipp: Bei Funktionenscharen erst allgemein ableiten, dann für spezielle Parameter-Werte konkrete Aussagen treffen.

Integralrechnung - Grundlagen

Das bestimmte Integral ∫ₐᵇ f(x)dx = $F(x)$ₐᵇ = F(b) - F(a) berechnet Flächen unter Kurven. Die Potenzregel lautet: Aus f(x) = xⁿ wird F(x) = 1/$n+1$ · xⁿ⁺¹.

Aufmerkung: Der Integralwert kann negativ sein, wenn die Funktion unterhalb der x-Achse verläuft. Für echte Flächeninhalte verwendest du Betragsstriche und teilst an Nullstellen auf.

Die Flächenbilanz zeigt, ob mehr Fläche ober- oder unterhalb der x-Achse liegt. Bei der Berechnung zwischen Nullstellen integrierst du abschnittsweise und addierst die Beträge.

Sachzusammenhänge: Aus der Geschwindigkeit wird durch Integration die Wegstrecke, aus der Zuflussrate die Wassermenge. Der Mittelwert einer Funktion ist m̄ = 1/$b-a$ · ∫ₐᵇ f(x)dx.

Merke: Integration ist die Umkehrung der Ableitung - prüfe dein Ergebnis durch Ableiten der Stammfunktion!

Integralrechnung - Erweitert

Uneigentliche Integrale treten auf, wenn eine Grenze gegen unendlich oder einen singulären Punkt geht. Du berechnest sie als Grenzwerte: lim(z→∞) ∫₁ᶻ f(x)dx.

Die Fläche zwischen zwei Graphen berechnest du mit A = ∫ₐᵇ |f(x) - g(x)|dx. Bestimme zuerst die Schnittpunkte, dann integriere die Differenzfunktion d(x) = f(x) - g(x).

Rotationsvolumen entstehen, wenn eine Fläche um die x-Achse rotiert: V = π∫ₐᵇ (f(x))²dx. Stelle dir vor, die Fläche wird in dünne Scheiben zerlegt, deren Volumen π·r²·h beträgt.

Bei unbegrenzten Flächen untersuchst du, ob der Grenzwert existiert. Nähert sich die Funktion schnell genug der Asymptote, hat die Fläche einen endlichen Inhalt.

Visualisierung hilft: Zeichne dir die Funktionen auf - so erkennst du schnell, welche Bereiche positiv oder negativ zum Integral beitragen.