Grundlagen und wichtige Formeln

Du kennst das sicher - manchmal brauchst du einfach schnell eine Formel oder eine mathematische Regel. Diese Seite ist wie ein Spickzettel mit den wichtigsten Basics.

Die binomische Formel $a+b$$a-b$ = a²-b² und der trigonometrische Zusammenhang sin²x + cos²x = 1 sind echte Klassiker in Prüfungen. Genauso wichtig sind die Summenformeln: 1+2+3+...+n = n$n+1$/2 für alle natürlichen Zahlen oder 1+3+5+...$2n-1$ = n² für ungerade Zahlen.

Diese Formeln tauchen oft als Bausteine in größeren Aufgaben auf. Wenn du sie auswendig kennst, sparst du dir wertvolle Zeit in der Prüfung.

💡 Tipp: Präge dir besonders die Summenformeln ein - die kommen garantiert dran!

Größen und Einheiten umrechnen

Einheiten umrechnen ist eigentlich total einfach, wenn du das System verstehst. Die Grundregel: Kleine Einheit → große Einheit = Komma nach links, große Einheit → kleine Einheit = Komma nach rechts.

Bei Längen gehst du in 10er-Schritten vor: mm → cm → dm → m → km. Bei Flächen sind es 100er-Schritte, bei Volumen 1000er-Schritte. Das Volumen hat noch eine Besonderheit: 1 dm³ = 1 Liter und 1 cm³ = 1 ml.

Prozent- und Zinsrechnung funktioniert mit drei Grundgrößen: Grundwert G, Prozentwert W und Prozentsatz p. Die Formel W = G·p/100 ist dein bester Freund. Bei Zinsen rechnest du mit Z = K·p·t/100, wobei ein Bankjahr 360 Tage hat.

Für Zinseszinsen brauchst du die Formel Kn = K₀ · $1 + p/100$ⁿ - das sind eigentlich Exponentialfunktionen.

💡 Tipp: Bei Prozentaufgaben kannst du auch direkt mit Dezimalzahlen rechnen: 30% von 90€ = 90 · 0,3 = 27€

Flächen und Körper - Die wichtigsten Formeln

Flächenberechnung ist viel einfacher, als es aussieht. Für Rechtecke gilt A = a·b, für Dreiecke A = (g·h)/2 und für Kreise A = π·r². Diese drei Grundformen reichen für fast alle Aufgaben.

Bei Körpern unterscheidest du zwischen Volumen und Oberfläche. Quader: V = a·b·c, Zylinder: V = π·r²·h, Pyramide: V = 1/3·G·h. Die Oberfläche berechnest du, indem du alle Teilflächen addierst.

Prismen haben die Grundfläche G und Höhe h, also V = G·h. Die Mantelfläche ist M = U·h $U = Umfang der Grundfläche$ und die Oberfläche O = 2·G + M.

Für zusammengesetzte Körper zerlegst du die Form in bekannte Grundkörper, berechnest einzeln und addierst. Bei Überschneidungen musst du diese Bereiche abziehen.

💡 Tipp: Zeichne dir komplizierte Körper immer auf und markiere die gegebenen Maße - das hilft beim Überblick!

Besondere Körper und Satz des Pythagoras

Der Kegel hat die Formeln V = 1/3·π·r²·h und die Kugel V = 4/3·π·r³. Diese Formeln musst du auswendig lernen, weil sie kompliziert herzuleiten sind.

Der Satz des Pythagoras $a² + b² = c²$ gilt nur in rechtwinkligen Dreiecken. Die längste Seite heißt Hypotenuse (c), die anderen beiden sind Katheten (a und b). Sie schließen den rechten Winkel ein.

Wenn du die Hypotenuse suchst: c = √$a² + b²$. Wenn du eine Kathete suchst: a = √$c² - b²$. Das funktioniert super für Entfernungen und Höhenberechnungen.

Zusammengesetzte Flächen zerlegst du in Grundformen, berechnest die Teilflächen einzeln und addierst sie. Beim Umfang zählst du nur die Außenlinien zusammen - nicht die inneren Trennlinien!

💡 Tipp: Kontrolliere beim Pythagoras immer, dass c die längste Seite ist - sonst hast du einen Fehler gemacht!

Diagramme verstehen und erstellen

Diagramme begegnen dir überall - in der Zeitung, in Statistiken und natürlich in Matheaufgaben. Die vier wichtigsten Typen sind Säulendiagramm (vertikale Balken), Balkendiagramm (horizontale Balken), Kreisdiagramm (Tortenstücke) und Streifendiagramm $100$.

Säulen- und Balkendiagramme zeigen absolute Werte - du kannst direkt ablesen, wie oft etwas vorkommt. Kreisdiagramme zeigen Anteile: Der ganze Kreis sind 100%, und jedes Stück zeigt einen Prozentanteil.

Streifendiagramme sind praktisch, wenn du verschiedene Gruppen vergleichen willst. Hier siehst du sofort die Verhältnisse - zum Beispiel 69% männlich, 31% weiblich.

Beim Erstellen von Diagrammen achte auf klare Beschriftung der Achsen und eine aussagekräftige Überschrift. Die Darstellung sollte ehrlich sein - keine verzerrten Achsen!

💡 Tipp: Bei Kreisdiagrammen rechnest du 360° ÷ 100% = 3,6°. Jedes Prozent entspricht also 3,6 Grad!

Stochastik - Wahrscheinlichkeit verstehen

Wahrscheinlichkeitsrechnung klingt kompliziert, ist aber logisch aufgebaut. Absolute Häufigkeit = wie oft etwas passiert (nur ganze Zahlen). Relative Häufigkeit = Anteil am Ganzen (Bruch, Dezimalzahl oder Prozent).

Die Formel: relative Häufigkeit = absolute Häufigkeit ÷ Gesamtzahl. Bei einem Laplace-Experiment sind alle Ergebnisse gleich wahrscheinlich - wie beim Würfeln. Jede Zahl hat die Wahrscheinlichkeit 1/6.

Baumdiagramme helfen bei mehrstufigen Experimenten. Die Pfadregeln sind dein Werkzeug: Produktregel - entlang eines Pfades multiplizieren, Summenregel - verschiedene Pfade addieren.

Die Grundformel: P(E) = Anzahl der günstigen Ergebnisse ÷ Anzahl aller möglichen Ergebnisse. Bei "ohne Zurücklegen" ändern sich die Wahrscheinlichkeiten nach jedem Zug.

💡 Tipp: Zeichne Baumdiagramme sauber auf - das verhindert Fehler bei komplexeren Aufgaben!

Vierfeldertafeln und bedingte Wahrscheinlichkeiten

Vierfeldertafeln verwendest du, wenn zwei Merkmale gleichzeitig untersucht werden und sich gegenseitig beeinflussen. Das nennt man bedingte Wahrscheinlichkeiten.

Die Tafel hat vier Felder: A∩B, A∩B̄, Ā∩B und Ā∩B̄. Die Randsummen ergeben immer 100%. Bedingte Wahrscheinlichkeit P(B|A) bedeutet: Wie wahrscheinlich ist B, wenn A bereits eingetreten ist?

Die Formel: P(B|A) = P(A∩B) ÷ P(A). Du teilst also die Wahrscheinlichkeit für beide Ereignisse durch die Wahrscheinlichkeit des ersten Ereignisses.

Beispiel: Von 10 Kugeln sind 4 grün, 6 blau. Von den grünen haben 3 Punkte, von den blauen 2. Dann ist P(Punkte|grün) = 3/4 = 75%.

Ob du erst die Farbe oder erst die Markierung ziehst, ist egal - das Endergebnis bleibt gleich.

💡 Tipp: Fülle die Vierfeldertafel systematisch aus - erst die gegebenen Werte, dann die Randsummen!

Statistische Berechnungen und Boxplots

Statistische Kennwerte fassen große Datenmengen zusammen. Das arithmetische Mittel (Durchschnitt) berechnest du: $x₁ + x₂ + ... + xₙ$ ÷ n. Einfach alle Werte addieren und durch die Anzahl teilen.

Der Median ist die Mitte der sortierten Daten. Bei ungerader Anzahl nimmst du den mittleren Wert, bei gerader Anzahl das arithmetische Mittel der beiden mittleren Werte. Die Spannweite ist Maximum minus Minimum.

Boxplots zeigen fünf wichtige Werte: Minimum, unteres Quartil, Median, oberes Quartil und Maximum. Zuerst sortierst du die Daten, dann bestimmst du diese fünf Werte und zeichnest die "Box" mit den "Whiskern" (Antennen).

Die Quartile teilen die Daten in vier gleiche Teile. 25% der Werte liegen unter dem unteren Quartil, 75% unter dem oberen Quartil.

💡 Tipp: Bei Boxplots siehst du sofort, ob die Daten symmetrisch verteilt sind oder schief!

Lineare Funktionen

Lineare Funktionen haben die Form f(x) = mx + b. Dabei ist m die Steigung und b der y-Achsenabschnitt. Diese beiden Werte bestimmen die Gerade vollständig.

Wenn du Punkt und Steigung gegeben hast, setzt du in die allgemeine Form ein. Bei P(1|3) und m = 2: 3 = 2·1 + b, also b = 1 und f(x) = 2x + 1.

Bei zwei Punkten berechnest du erst die Steigung: m = $y₂ - y₁$ ÷ $x₂ - x₁$. Dann setzt du einen Punkt ein, um b zu finden. Mit P₁(3|1) und P₂(9|7) ergibt das m = 6÷6 = 1 und b = -2.

Die Steigung kannst du auch grafisch ablesen: Wie viele Einheiten nach oben pro Einheit nach rechts? Eine Steigung von 2 bedeutet: 2 nach oben, 1 nach rechts.

💡 Tipp: Positive Steigung = Gerade steigt an, negative Steigung = Gerade fällt ab!

Schnittpunkte und Nullstellen

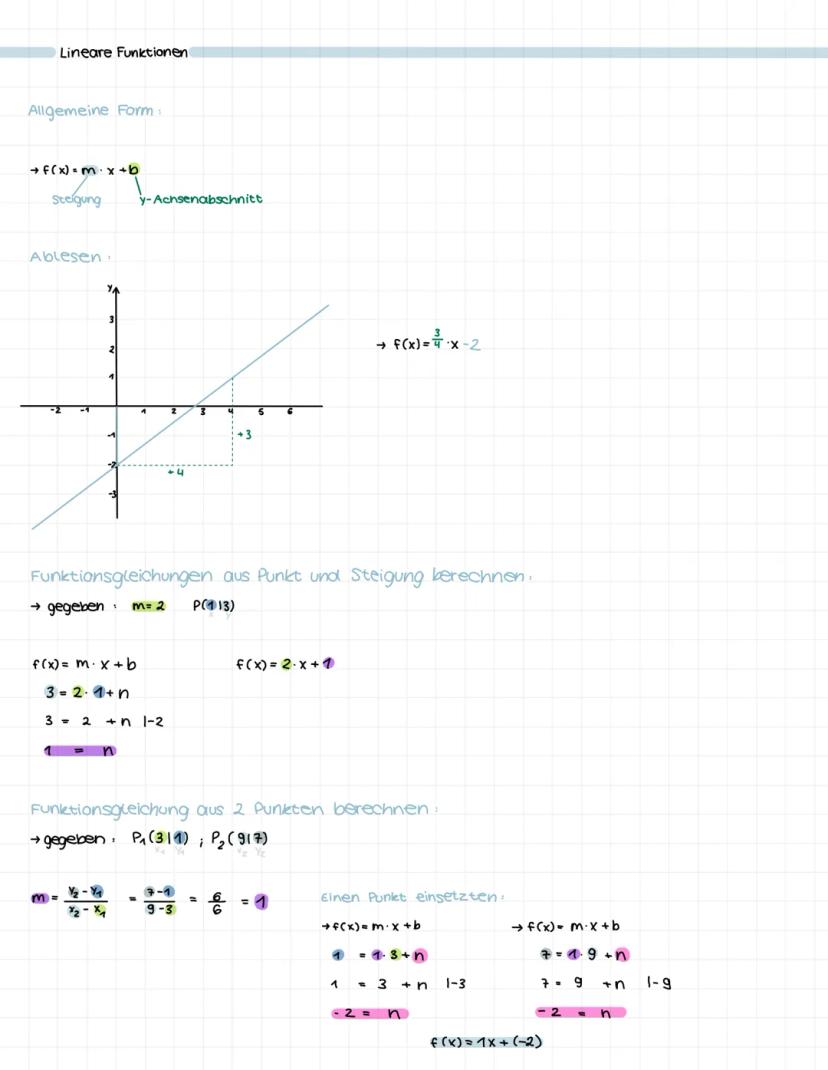
Schnittpunkte zweier Geraden findest du mit dem Gleichsetzungsverfahren: f(x) = g(x). Du löst nach x auf und setzt das Ergebnis in eine der beiden Funktionen ein.

Beispiel: -0,5x + 2 = x - 1. Umformen ergibt x = 2, und f(2) = 1, also S(2|1). Das funktioniert bei allen linearen Gleichungssystemen.

Nullstellen berechnest du mit f(x) = 0. Bei linearen Funktionen ax + c = 0 stellst du einfach um: x = -c/a. Bei quadratischen Funktionen ax² + c = 0 gibt es meist zwei Lösungen: x = ±√$-c/a$.

Scheitelpunktform a$x-d$² + e = 0 löst du schrittweise: Erst nach $x-d$² umstellen, dann Wurzel ziehen. Das ergibt x-d = ±√(...), also zwei Werte für x.

Bei quadratischen Funktionen können null, eine oder zwei Nullstellen existieren - je nachdem, ob die Parabel die x-Achse schneidet.

💡 Tipp: Kontrolliere deine Nullstellen, indem du sie in die ursprüngliche Funktion einsetzt - das Ergebnis muss 0 sein!