Quadratische Funktionen und die Normalparabel

Eine quadratische Funktion hat immer die Form f$x$ = ax² + bx + c, wobei a ≠ 0 ist. Das x² macht den entscheidenden Unterschied zu linearen Funktionen - deshalb entstehen auch die typischen U-förmigen Kurven, die Parabeln.

Die einfachste quadratische Funktion ist f$x$ = x², deren Graph die Normalparabel heißt. Sie hat ihren tiefsten Punkt (den Scheitelpunkt) im Ursprung (0|0) und öffnet sich nach oben. Die Parabel ist perfekt symmetrisch zur y-Achse.

Bei der Normalparabel gilt: Je weiter du dich vom Scheitelpunkt entfernst, desto steiler wird die Kurve. Links vom Scheitelpunkt fällt sie, rechts davon steigt sie. Die Wertemenge umfasst alle Zahlen ≥ 0, da der niedrigste y-Wert bei 0 liegt.

Merktipp: Die Normalparabel f$x$ = x² ist dein Grundbaustein - alle anderen Parabeln entstehen durch Verschiebungen und Streckungen davon!

Nullstellen und verschobene Parabeln

Nullstellen sind die Stellen, wo deine Parabel die x-Achse schneidet (also wo f$x$ = 0 ist). Je nach Form kann eine Parabel 0, 1 oder 2 Nullstellen haben - das siehst du sofort am Graphen.

Wenn du eine Parabel vertikal verschiebst mit f$x$ = x² + e, bewegst du sie einfach nach oben (e > 0) oder unten (e < 0). Der Scheitelpunkt wandert von (0|0) zu (0|e), aber die Form bleibt gleich.

Bei horizontalen Verschiebungen mit f$x$ = $x - d$² wird's etwas tricky: Ist d > 0, geht die Parabel nach rechts, ist d < 0, nach links. Der Scheitelpunkt liegt dann bei (d|0). Wichtig: Das Vorzeichen in der Klammer wirkt umgekehrt!

Praxistipp: Bei f$x$ = $x - 3$² + 2 ist der Scheitelpunkt bei (3|2) - einfach die Vorzeichen in der Klammer umdrehen!

Scheitelpunktform und Streckungen

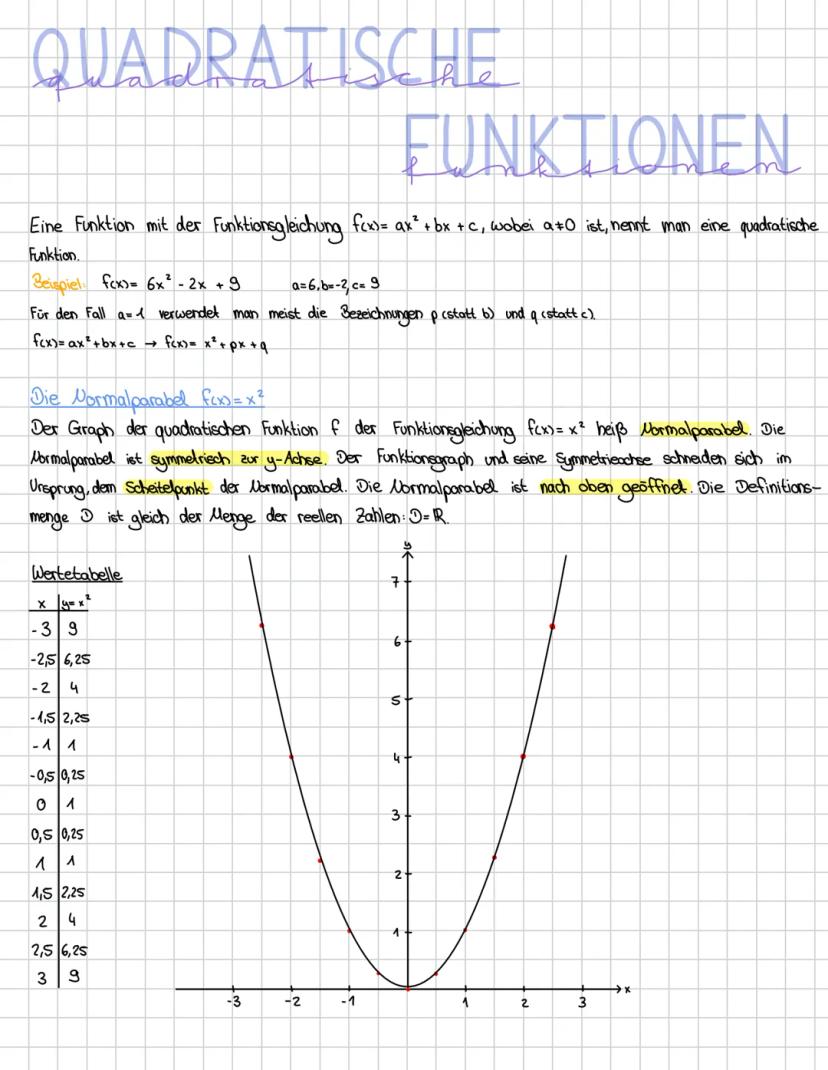
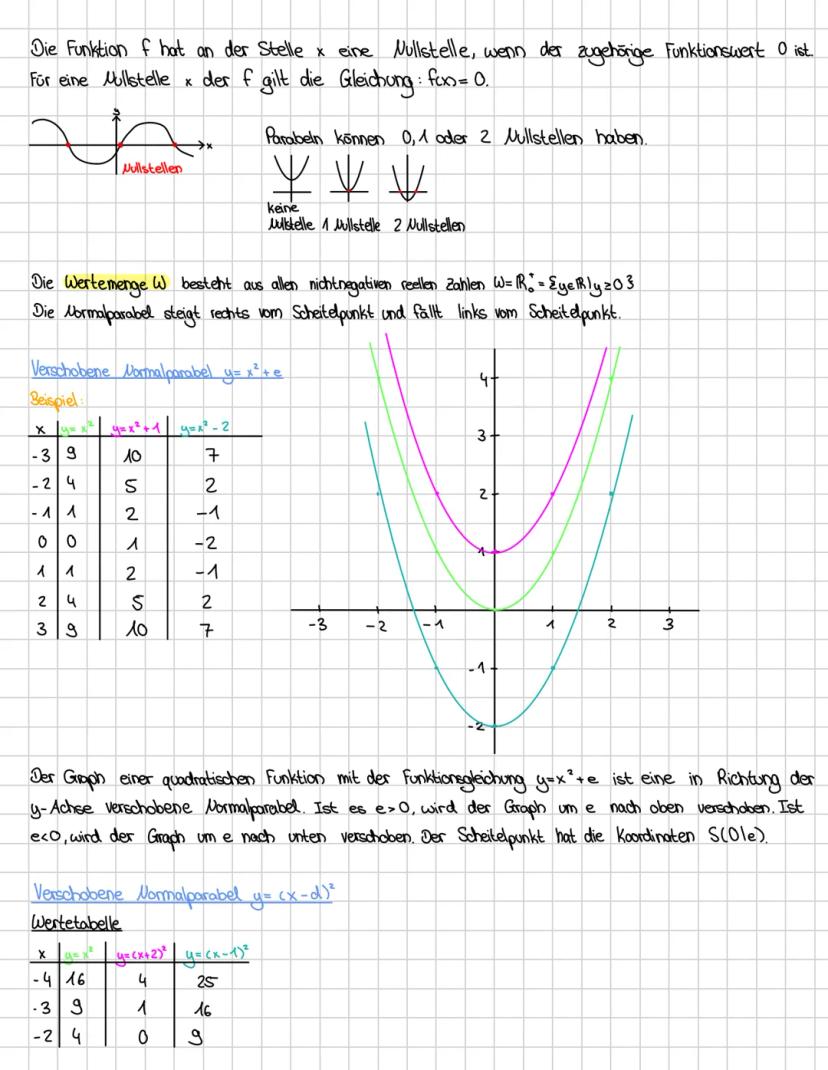
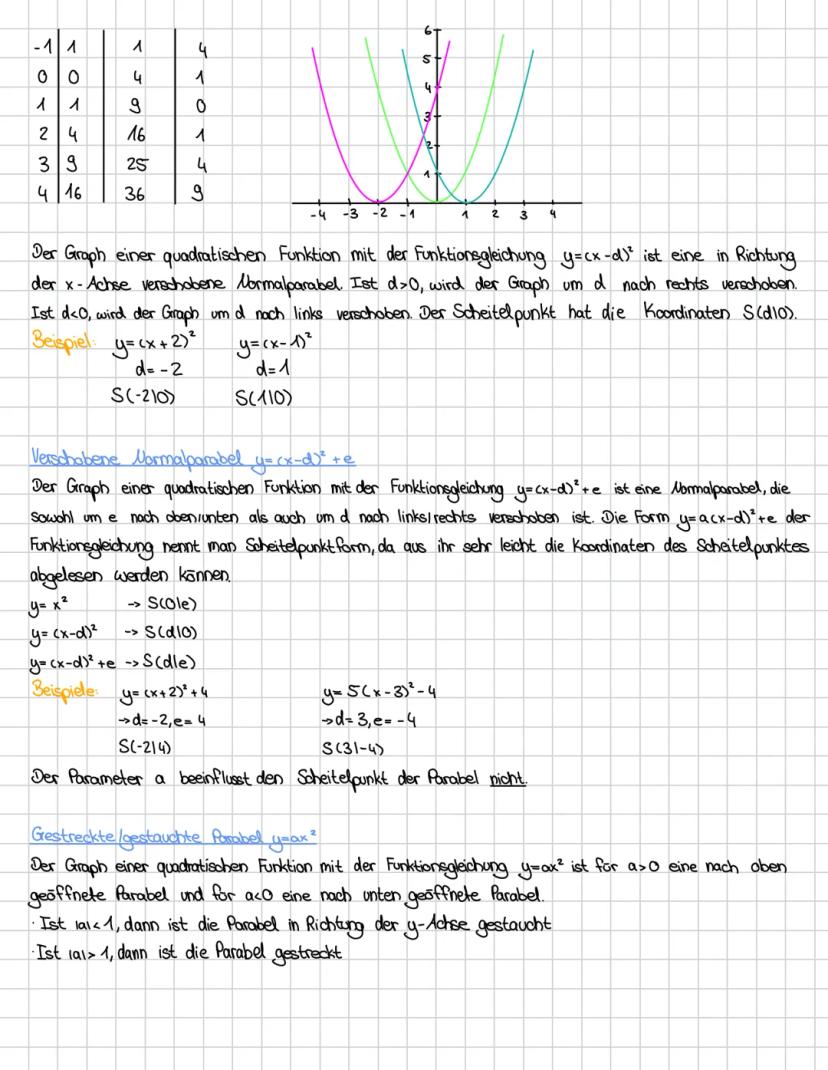
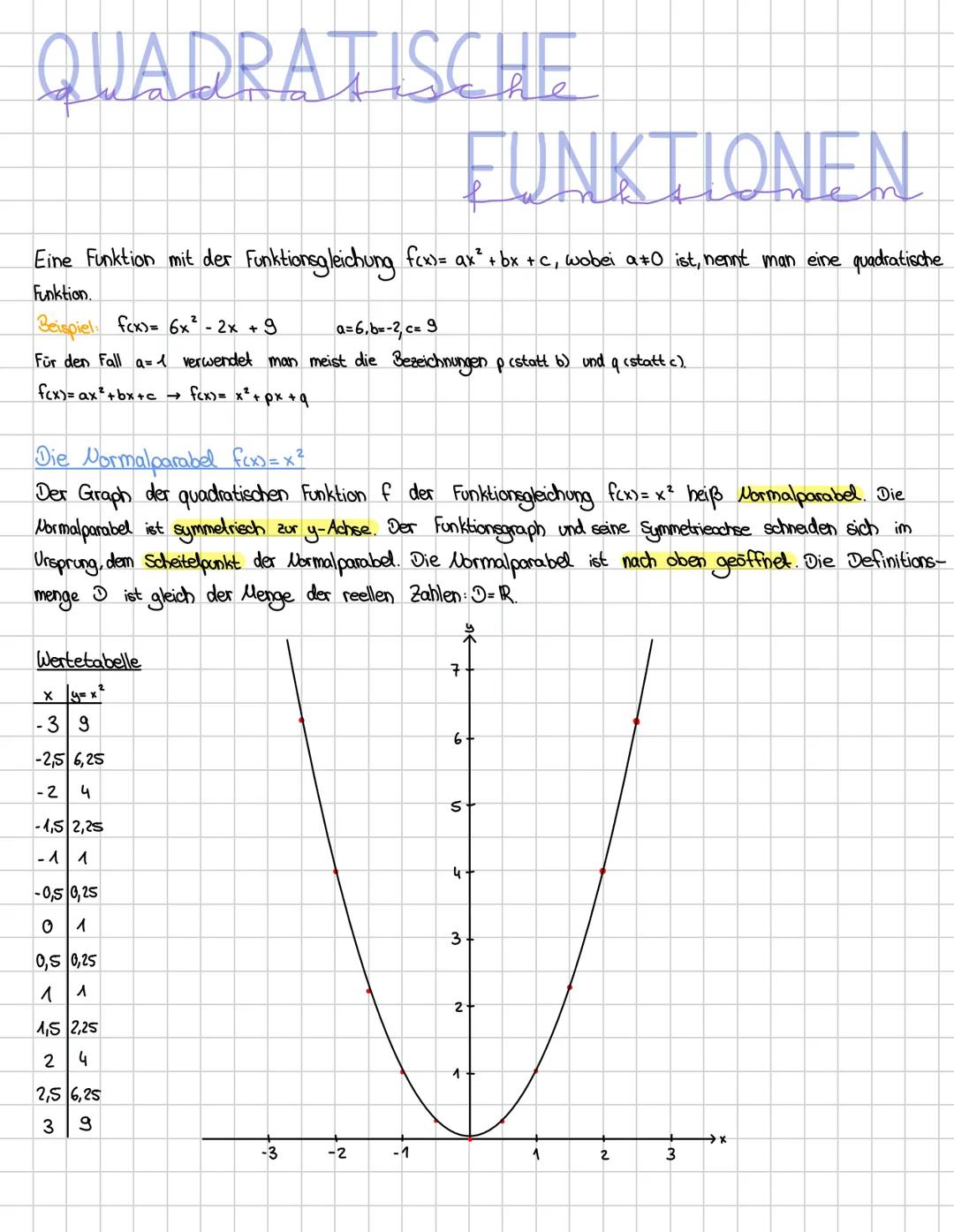
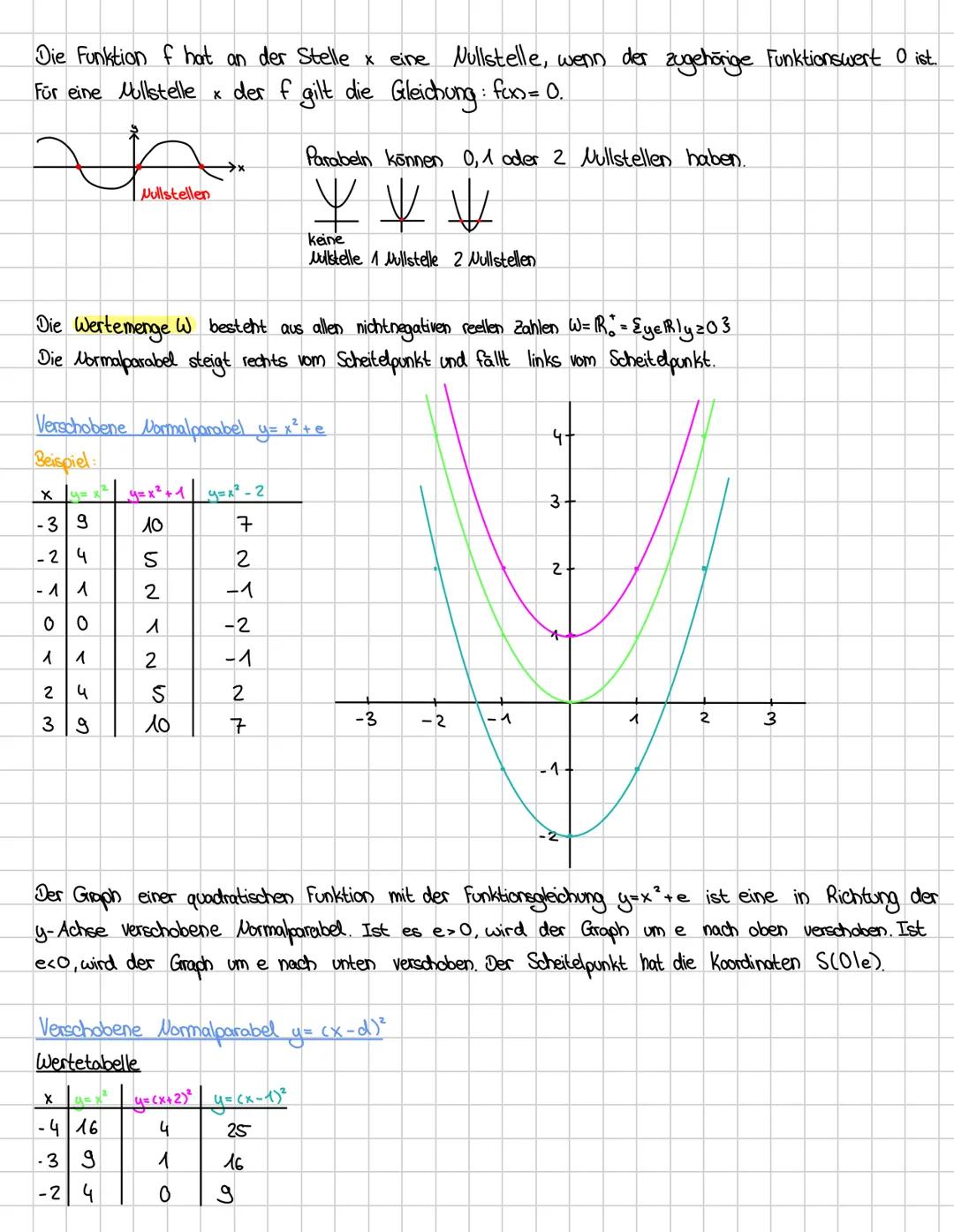
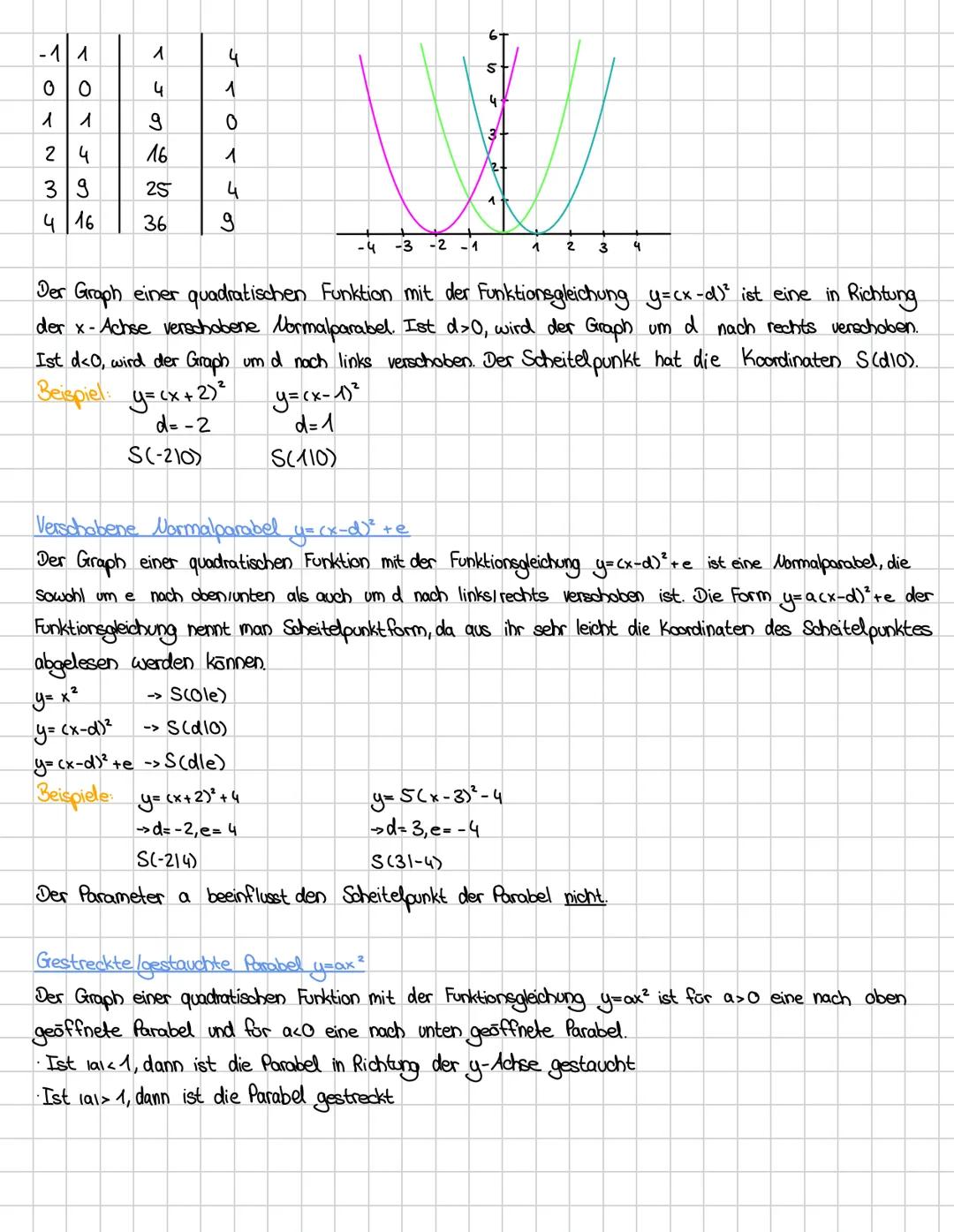
Die Scheitelpunktform f$x$ = a$x - d$² + e ist mega praktisch, weil du sofort den Scheitelpunkt S(d|e) ablesen kannst. Diese Form zeigt dir auf einen Blick, wohin deine Parabel verschoben wurde.

Der Parameter a bestimmt, wie deine Parabel aussieht: Ist a > 0, öffnet sie sich nach oben, ist a < 0, nach unten. Je größer |a|, desto schmaler wird die Parabel (gestreckt). Ist |a| < 1, wird sie breiter (gestaucht).

Beispiele gefällig? Bei f$x$ = $x + 2$² + 4 liegt der Scheitelpunkt bei $-2|4$. Bei f$x$ = 5$x - 3$² - 4 findest du ihn bei $3|-4$. Der Faktor 5 macht die Parabel schmal und steil.

Die Umwandlung von der allgemeinen Form zur Scheitelpunktform gelingt mit der quadratischen Ergänzung - du ergänzt geschickt, um eine binomische Formel zu erhalten.

Eselsbrücke: In der Scheitelpunktform kannst du den Scheitelpunkt direkt ablesen - das macht Aufgaben oft viel einfacher!

Umwandlung zwischen den Formen

Um von der allgemeinen Form f$x$ = x² + px + q zur Scheitelpunktform zu kommen, nutzt du die quadratische Ergänzung. Das klingt komplizierter als es ist!

Die Regel ist einfach: Du nimmst die Hälfte von p, quadrierst sie - das ist deine quadratische Ergänzung $p/2$². Diese addierst und subtrahierst du gleichzeitig, damit sich nichts ändert.

Beispiel: f$x$ = x² + 10x + 3 wird zu f$x$ = x² + 10x + 25 - 25 + 3 = $x + 5$² - 22. Fertig! Der Scheitelpunkt liegt bei $-5|-22$.

Wenn du eine Funktionsgleichung aus zwei Punkten erstellst, setzt du beide Punkte in die allgemeine Form ein und löst das entstehende Gleichungssystem. Das gibt dir die Parameter p und q.

Rechentrick: Bei der quadratischen Ergänzung immer $p/2$² - das ist die magische Formel, die du brauchst!

Quadratische Gleichungen lösen

Quadratische Gleichungen haben die Form x² + px + q = 0 und können 0, 1 oder 2 Lösungen haben. Du erkennst sie daran, dass die höchste Potenz von x eine 2 ist.

Für spezielle Fälle gibt's Abkürzungen: Bei x² + q = 0 löst du einfach nach x² auf. Ist q > 0, gibt's keine Lösung (negative Wurzel). Ist q ≤ 0, hast du 1 oder 2 Lösungen.

Bei x² + px = 0 klammerst du x aus: x$x + p$ = 0. Nach dem Satz vom Nullprodukt muss einer der Faktoren null sein, also x = 0 oder x = -p.

Für die allgemeine quadratische Gleichung hast du zwei Methoden: quadratische Ergänzung oder die pq-Formel. Die pq-Formel ist meist schneller: x₁,₂ = -p/2 ± √$(p/2)² - q$.

Entscheidungshilfe: Die Diskriminante D = $p/2$² - q zeigt dir sofort: D > 0 bedeutet 2 Lösungen, D = 0 eine Lösung, D < 0 keine Lösung!

Die pq-Formel und der Satz vom Nullprodukt

Die pq-Formel x₁,₂ = -p/2 ± √$(p/2)² - q$ ist dein Allzweck-Werkzeug für quadratische Gleichungen. Sie funktioniert immer, wenn du die Gleichung in die Normalform x² + px + q = 0 gebracht hast.

Der Satz vom Nullprodukt besagt: Wenn ein Produkt null ist, muss mindestens ein Faktor null sein. Das nutzt du bei Gleichungen wie x + 2$$x - 2 = 0 - dann ist x = -2 oder x = 2.

Die Diskriminante D = $p/2$² - q ist wie ein Detector: Sie verrät dir vor dem Rechnen, ob und wie viele Lösungen existieren. Negative Diskriminante? Keine reelle Lösung!

Bei Bruchgleichungen mit quadratischen Termen multiplizierst du zuerst mit dem Hauptnenner, um die Brüche wegzubekommen. Dann wendest du die gewohnten Methoden an.

Prüf-Tipp: Setze deine Lösungen immer in die ursprüngliche Gleichung ein - so erkennst du Rechenfehler sofort!

Herleitung und der Satz von Vieta

Die pq-Formel entsteht durch quadratische Ergänzung an der allgemeinen Gleichung x² + px + q = 0. Dieser Weg zeigt dir, warum die Formel funktioniert - nicht nur wie.

Die Diskriminante D = $p/2$² - q entscheidet über die Anzahl der Lösungen. Das macht mathematisch Sinn: Unter der Wurzel darf nichts Negatives stehen, wenn du reelle Zahlen suchst.

Bei Bruchgleichungen wie -2x/$2-2x²$ = 3/$1-3x$ multiplizierst du kreuzweise und bringst alles auf eine Seite. Dann löst du die entstehende quadratische Gleichung normal.

Der Satz von Vieta ist ein cleverer Trick: Wenn x₁ und x₂ Lösungen von x² + px + q = 0 sind, dann gilt p = -$x₁ + x₂$ und q = x₁ · x₂. Das hilft beim Prüfen und beim Aufstellen von Gleichungen.

Anwendung: Mit Vieta kannst du schnell prüfen, ob deine berechneten Lösungen stimmen - einfach addieren und multiplizieren!

Der Satz von Vieta in der Praxis

Der Satz von Vieta verbindet die Lösungen einer quadratischen Gleichung mit ihren Parametern: p = -$x₁ + x₂$ und q = x₁ · x₂. Das ist wie ein mathematischer Fingerabdruck!

Du kannst ihn in zwei Richtungen nutzen: Entweder checkst du deine berechneten Lösungen oder stellst zu gegebenen Lösungen die passende Gleichung auf. Beide Wege sparen Zeit und verhindern Fehler.

Beispiel zur Kontrolle: Bei x² + 8x + 12 = 0 mit den Lösungen x₁ = -2 und x₂ = -6 prüfst du: -$-2 + (-6)$ = 8 ✓ und $-2$ · $-6$ = 12 ✓. Passt!

Der Beweis funktioniert über die Produktform x - x₁$$x - x₂ = 0, die du ausmultiplizierst. So siehst du, woher die Vieta-Formeln kommen.

Zeitsparer: Nutze Vieta als Schnellcheck für deine Lösungen - oft erkennst du schon beim Hinschauen, ob das Ergebnis stimmen kann!