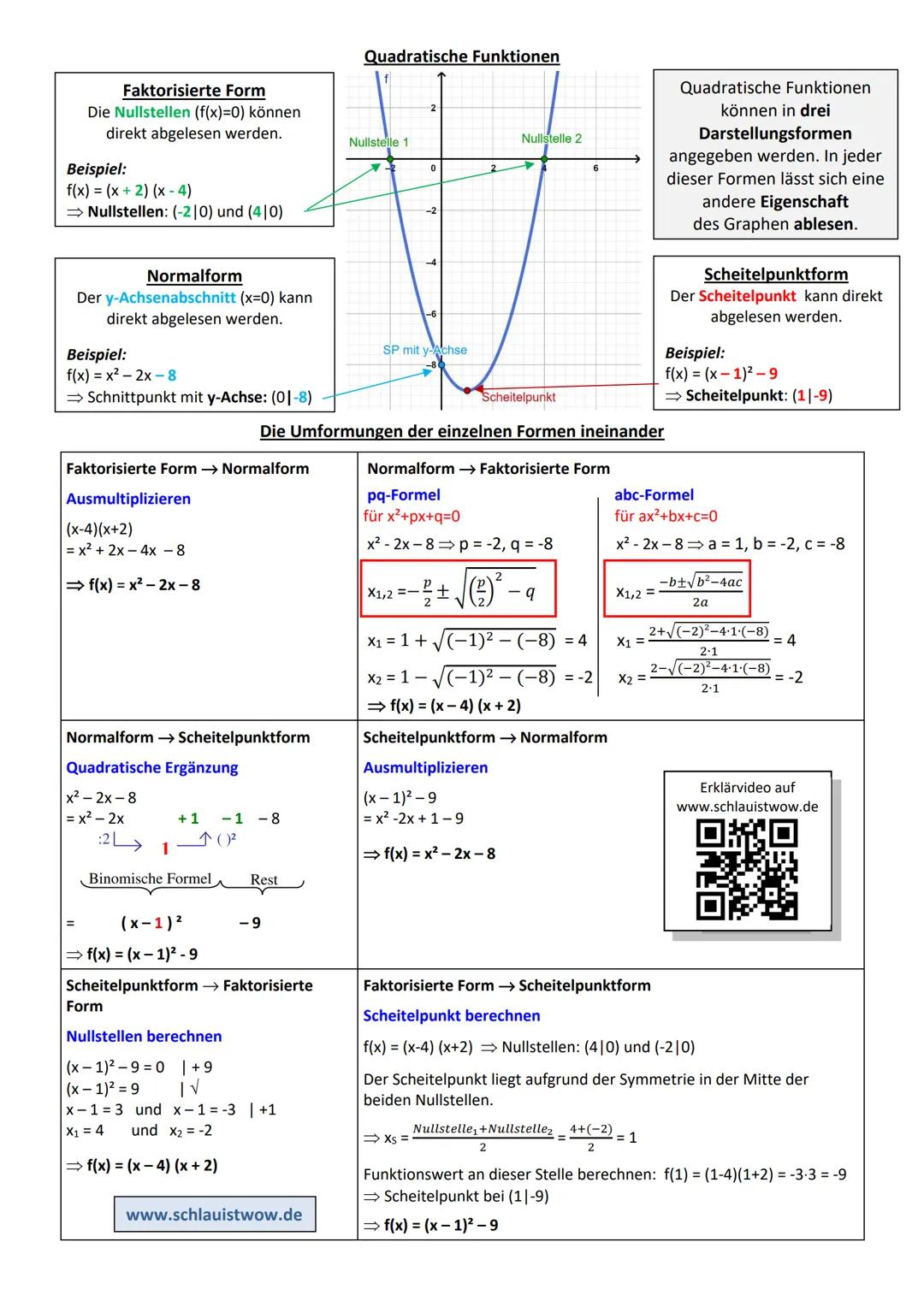
Die drei Darstellungsformen quadratischer Funktionen

Jede quadratische Funktion kann in drei verschiedenen Formen geschrieben werden - wie drei verschiedene Sprachen für dieselbe mathematische Aussage. Je nachdem, was du wissen willst, ist eine Form praktischer als die anderen.

Die faktorisierte Form f$x$ = x + 2$$x - 4 zeigt dir sofort die Nullstellen. Hier siehst du direkt: Die Parabel schneidet die x-Achse bei x = -2 und x = 4. Super praktisch, wenn du schnell wissen willst, wo der Graph die x-Achse kreuzt!

Bei der Normalform f$x$ = x² - 2x - 8 kannst du den y-Achsenabschnitt direkt ablesen - hier ist es -8. Die Scheitelpunktform f$x$ = $x - 1$² - 9 verrät dir sofort den höchsten oder tiefsten Punkt: Der Scheitelpunkt liegt bei $1|-9$.

Merktipp: Faktorisiert = Nullstellen, Normal = y-Achse, Scheitelpunkt = Extrempunkt!

Umformen zwischen den Formen ist dein Werkzeugkasten: Von faktorisiert zu normal multiplizierst du aus. Von normal zu faktorisiert nutzt du die pq-Formel oder abc-Formel. Für die Scheitelpunktform brauchst du die quadratische Ergänzung - klingt kompliziert, ist aber nur ein Trick zum Umformen!