Trigonometrie - Die Grundlagen für rechtwinklige Dreiecke
Stell dir vor, du willst die Höhe eines Gebäudes messen, ohne hochzuklettern - Trigonometrie macht's möglich! In jedem rechtwinkligen Dreieck mit einem spitzen Winkel α bleiben die Seitenverhältnisse immer gleich.
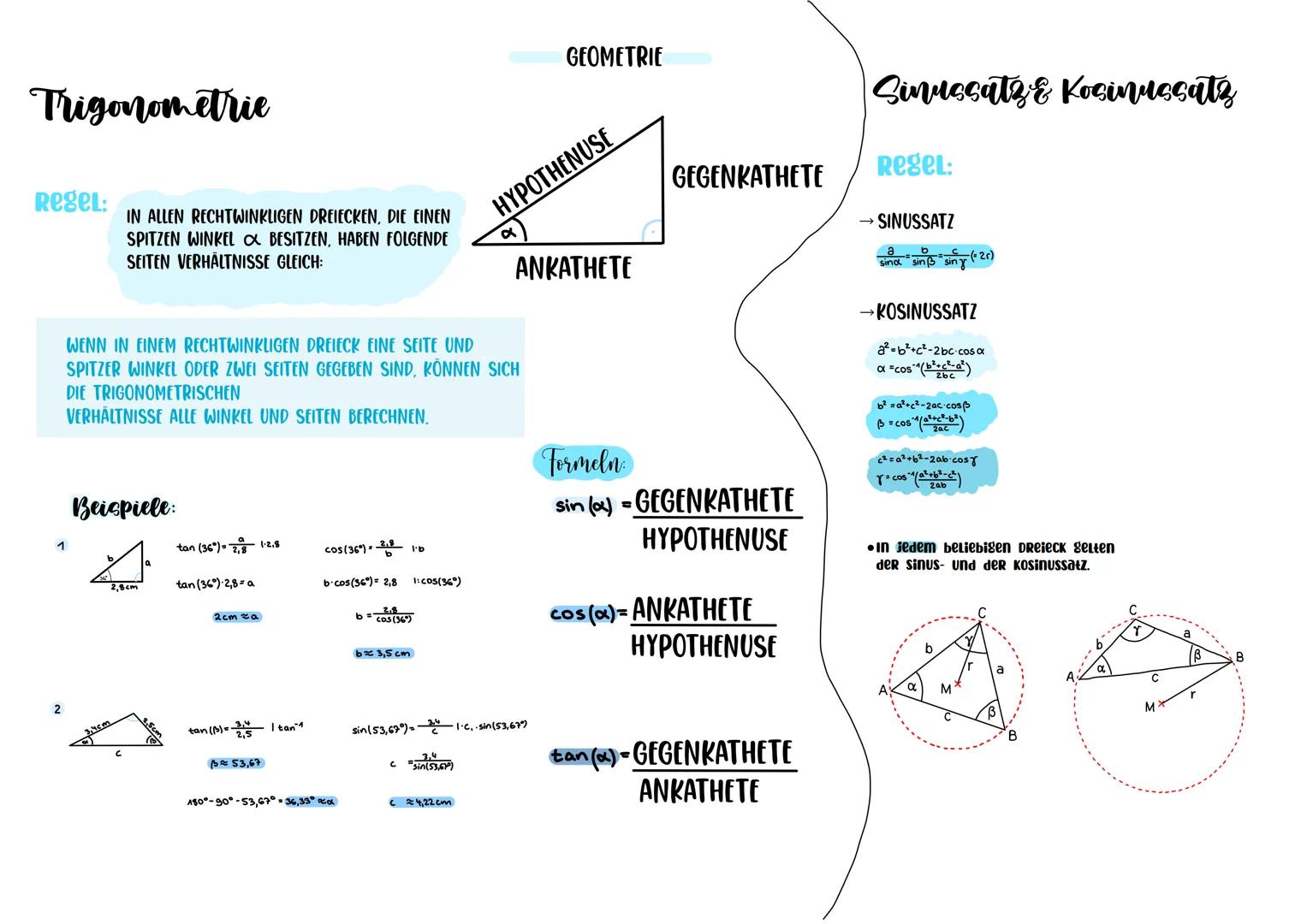
Die drei wichtigsten Formeln musst du dir merken:
- sin(α) = Gegenkathete / Hypotenuse
- cos(α) = Ankathete / Hypotenuse
- tan(α) = Gegenkathete / Ankathete
Gegenkathete liegt dem Winkel α gegenüber, Ankathete liegt daneben, und die Hypotenuse ist immer die längste Seite. Wenn du eine Seite und einen spitzen Winkel kennst (oder zwei Seiten), kannst du alle anderen Werte berechnen.
💡 Merktipp: SoH-CaH-ToA hilft beim Merken - Sinus = opposite/Hypotenuse, Cosinus = adjacent/Hypotenuse, Tangens = opposite/adjacent!
Bei den Beispielen siehst du, wie's funktioniert: Mit tan(36°) = 2,8/a findest du a ≈ 2cm. Der Sinussatz und Kosinussatz erweitern diese Möglichkeiten auf beliebige Dreiecke - auch ohne rechten Winkel! Der Sinussatz lautet a/sin α = b/sin β = c/sin γ, während der Kosinussatz wie eine erweiterte Version des Satzes von Pythagoras funktioniert.