Umkehrfunktion rechnerisch bestimmen

Die Umkehrfunktion zu finden ist eigentlich ganz einfach, wenn du die zwei Grundschritte befolgst. Bei der Funktion f(x) = 2x - 1 siehst du, wie's funktioniert.

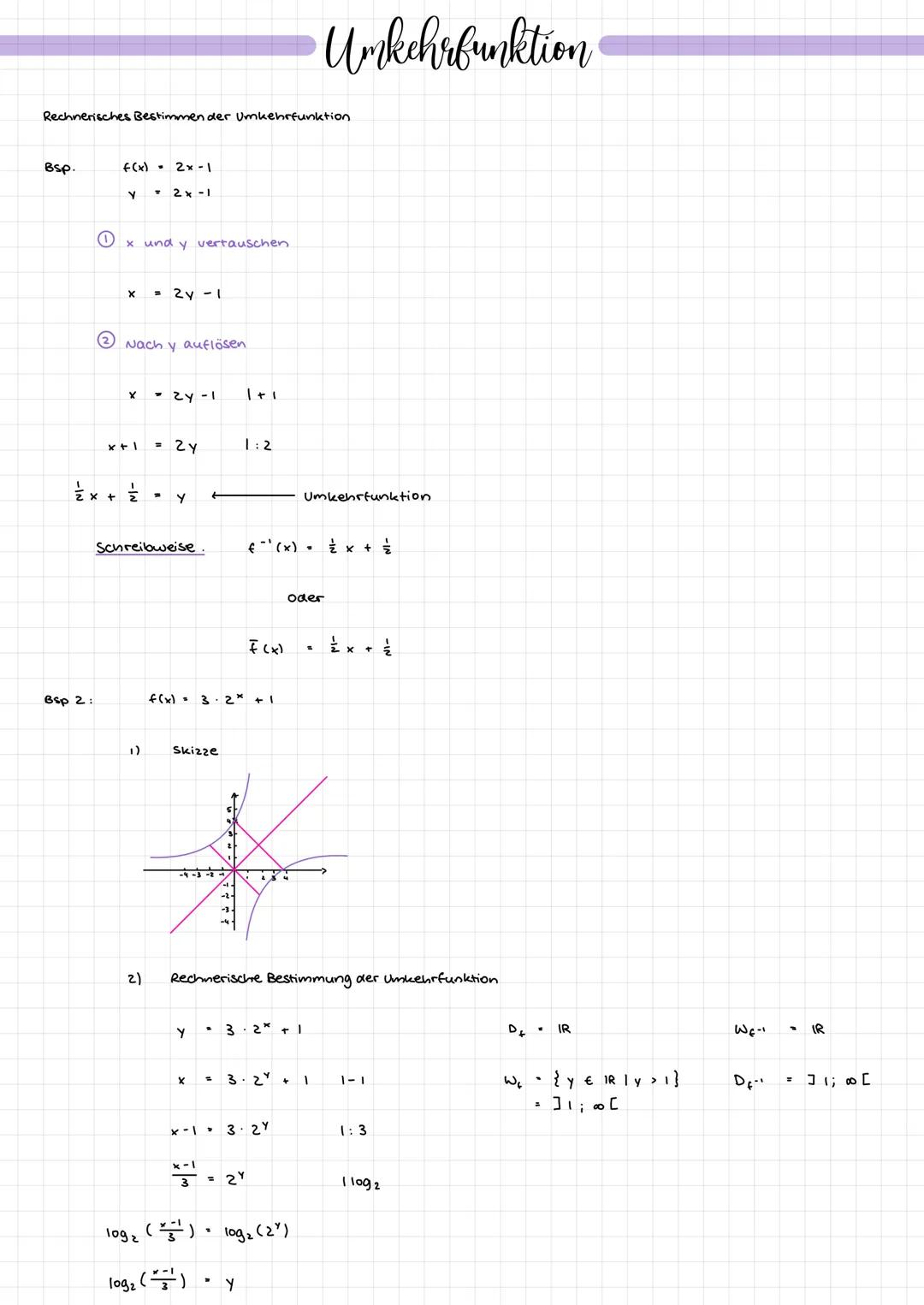
Schritt 1: Schreibe f(x) als y = 2x - 1 und vertausche x und y. Aus y = 2x - 1 wird dann x = 2y - 1.

Schritt 2: Löse die Gleichung nach y auf. Du addierst 1 auf beiden Seiten: x + 1 = 2y. Dann teilst du durch 2 und erhältst y = ½x + ½.

Merktipp: Die Umkehrfunktion "macht rückgängig", was die ursprüngliche Funktion tut!

Die Schreibweise für Umkehrfunktionen ist f⁻¹(x) = ½x + ½ oder f̄(x) = ½x + ½. Das kleine "-1" bedeutet nicht "hoch minus eins", sondern zeigt die Umkehrfunktion an.

Komplexeres Beispiel mit Exponentialfunktion

Bei f(x) = 3 · 2ˣ + 1 wird's interessanter, weil hier Logarithmen ins Spiel kommen. Der Definitionsbereich Df ist alle reellen Zahlen, aber der Wertebereich Wf ist nur ]1;∞[, da Exponentialfunktionen nie null werden.

Wieder die zwei Schritte: Aus y = 3 · 2ˣ + 1 wird x = 3 · 2ʸ + 1. Jetzt löst du nach y auf: x - 1 = 3 · 2ʸ, dann $x-1$/3 = 2ʸ.

Um y zu isolieren, brauchst du den Logarithmus zur Basis 2: log₂$(x-1)/3$ = y. Das ist deine Umkehrfunktion! Wichtig: Der Definitionsbereich der Umkehrfunktion entspricht dem Wertebereich der ursprünglichen Funktion.