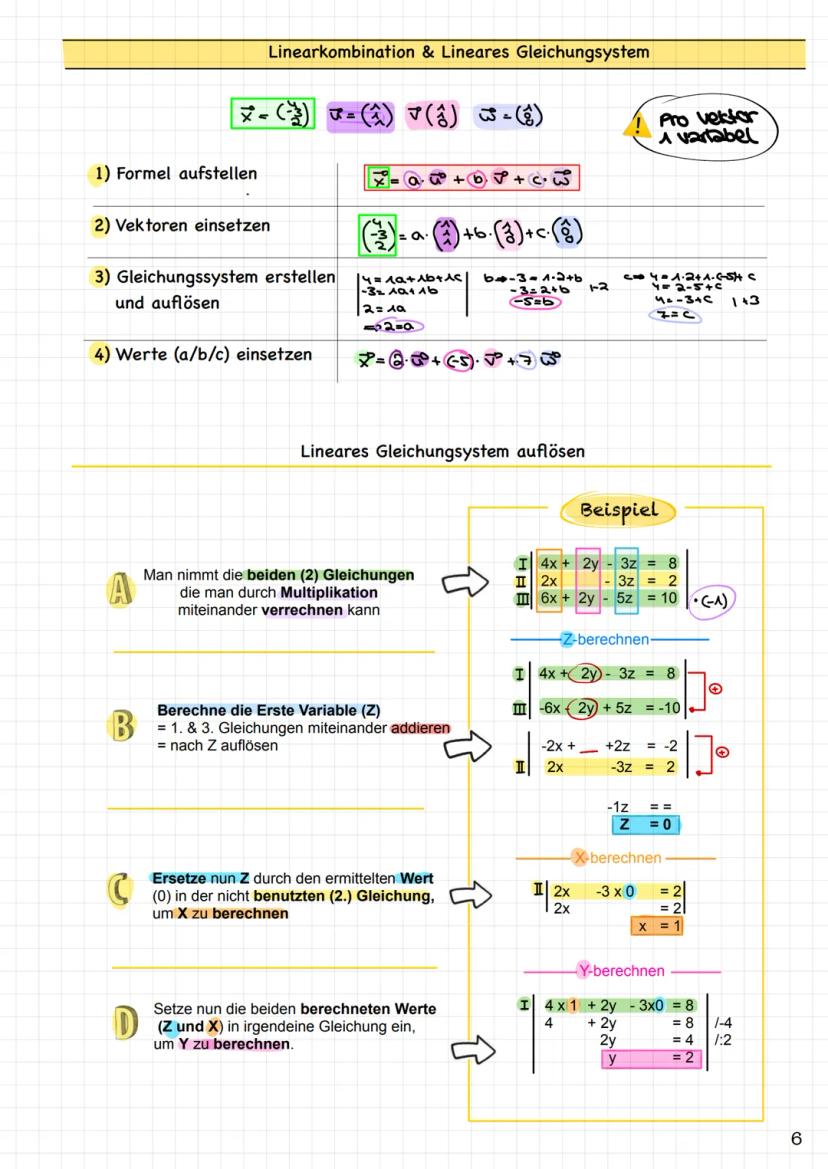
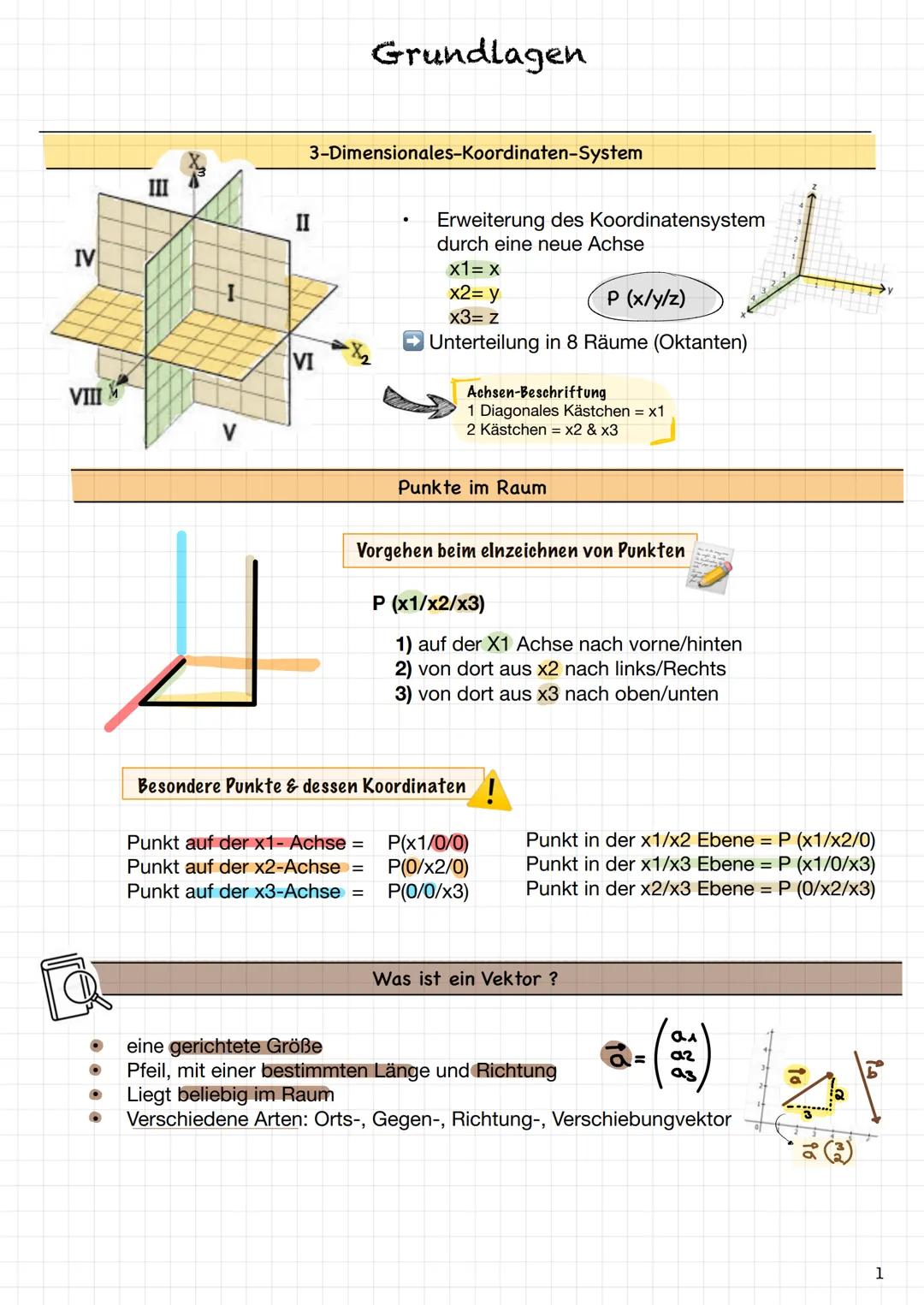
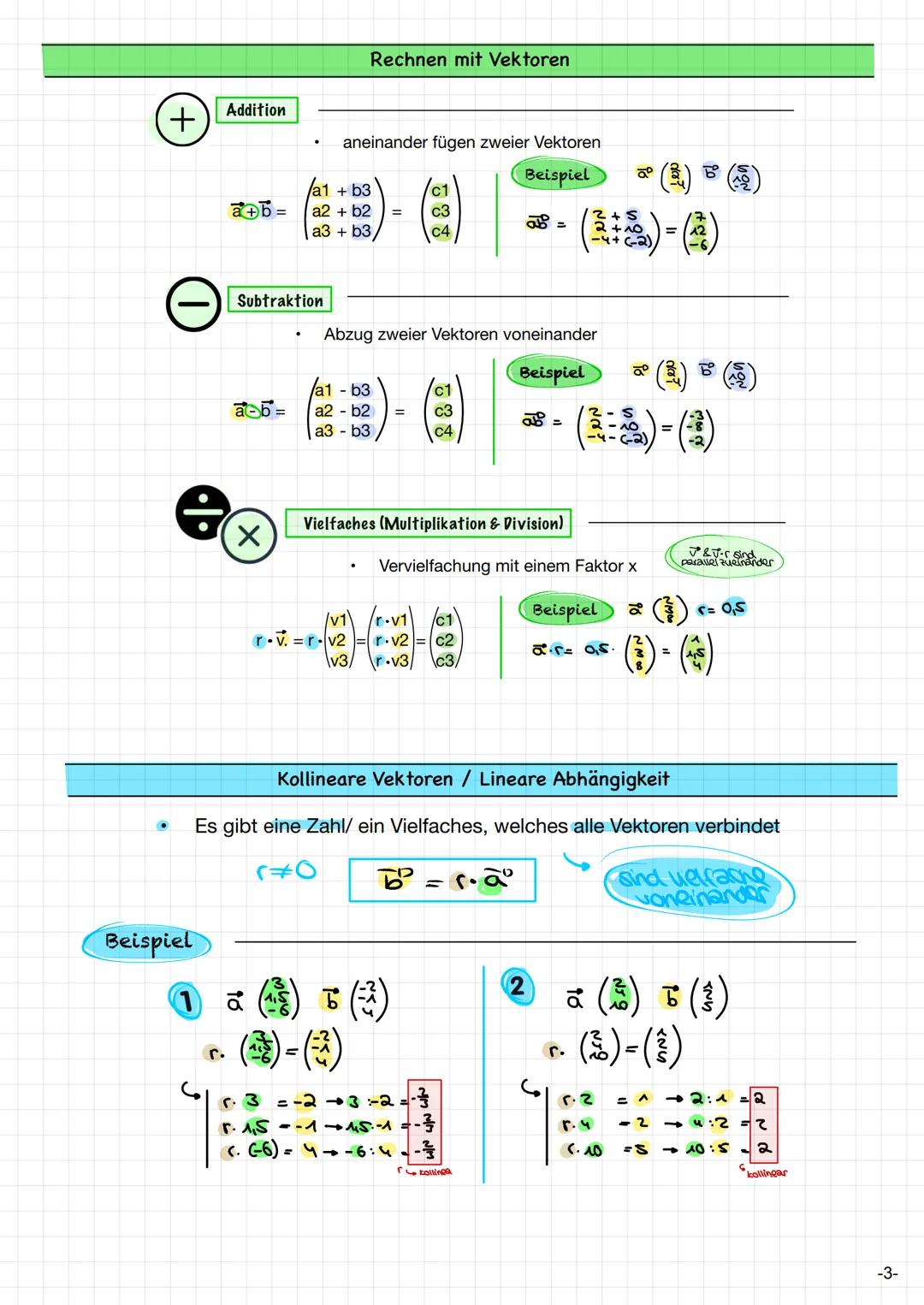
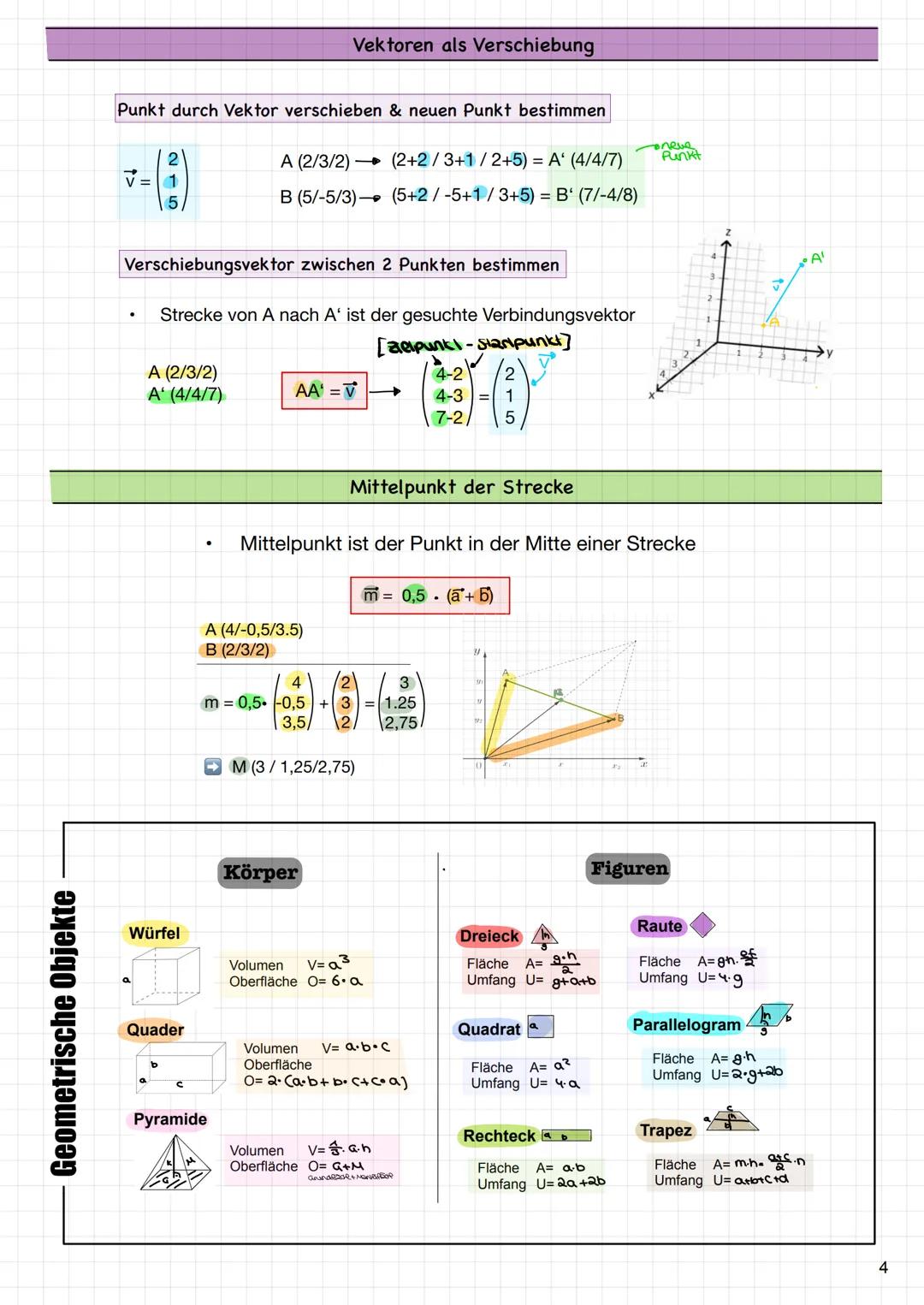
Rechnen mit Vektoren
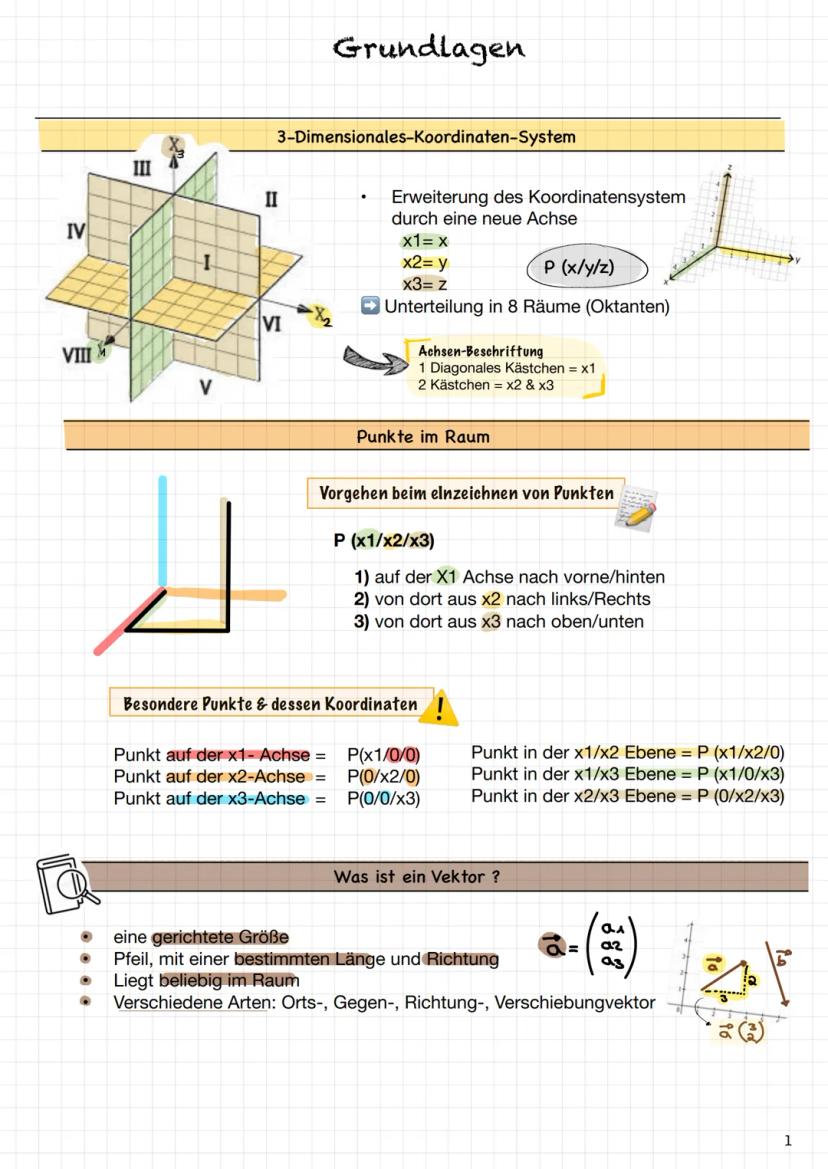
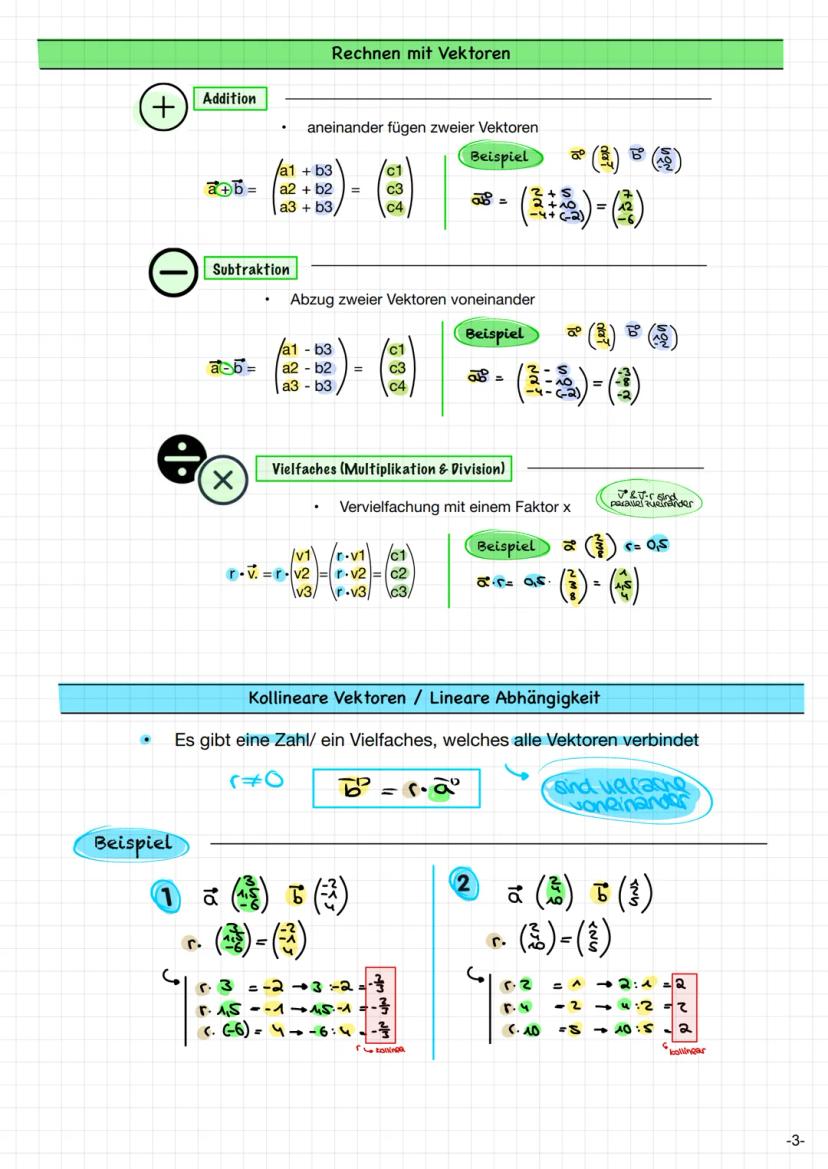
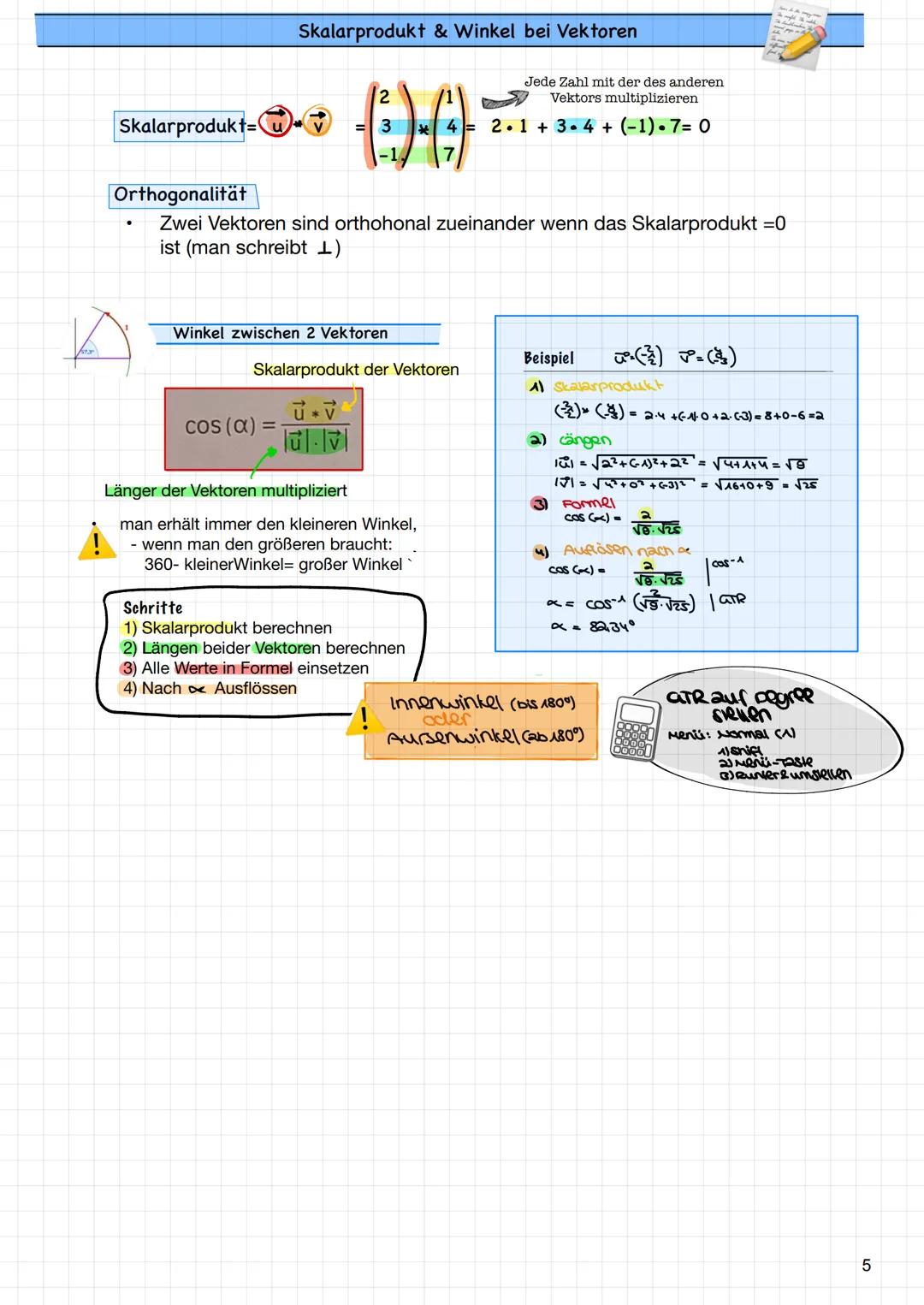
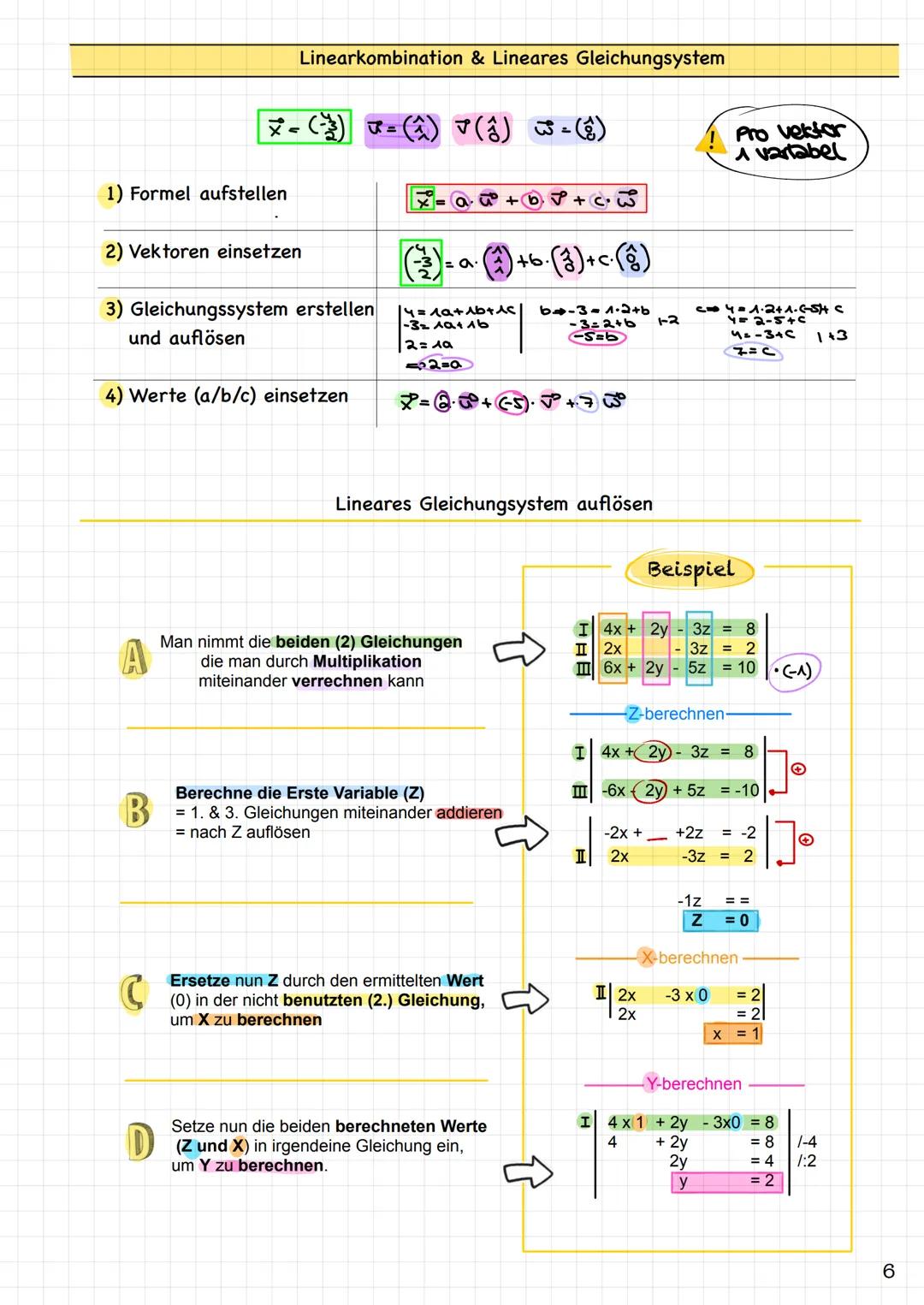
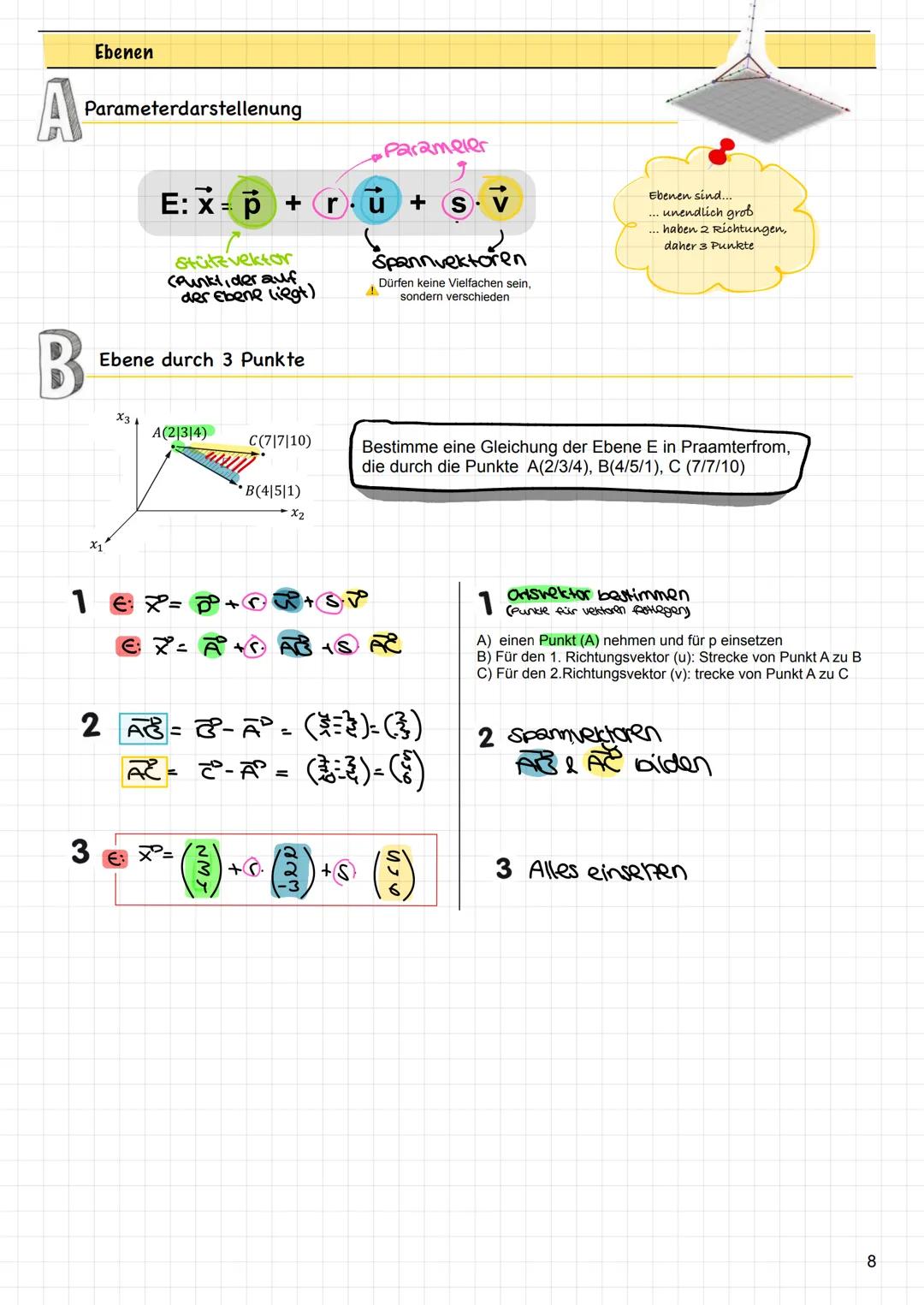
Vektorrechnung funktioniert komponentenweise - das heißt, du rechnest einfach die entsprechenden Zahlen zusammen oder voneinander ab. Bei der Addition addierst du a₁+b₁, a₂+b₂, a₃+b₃. Bei der Subtraktion ziehst du entsprechend ab.
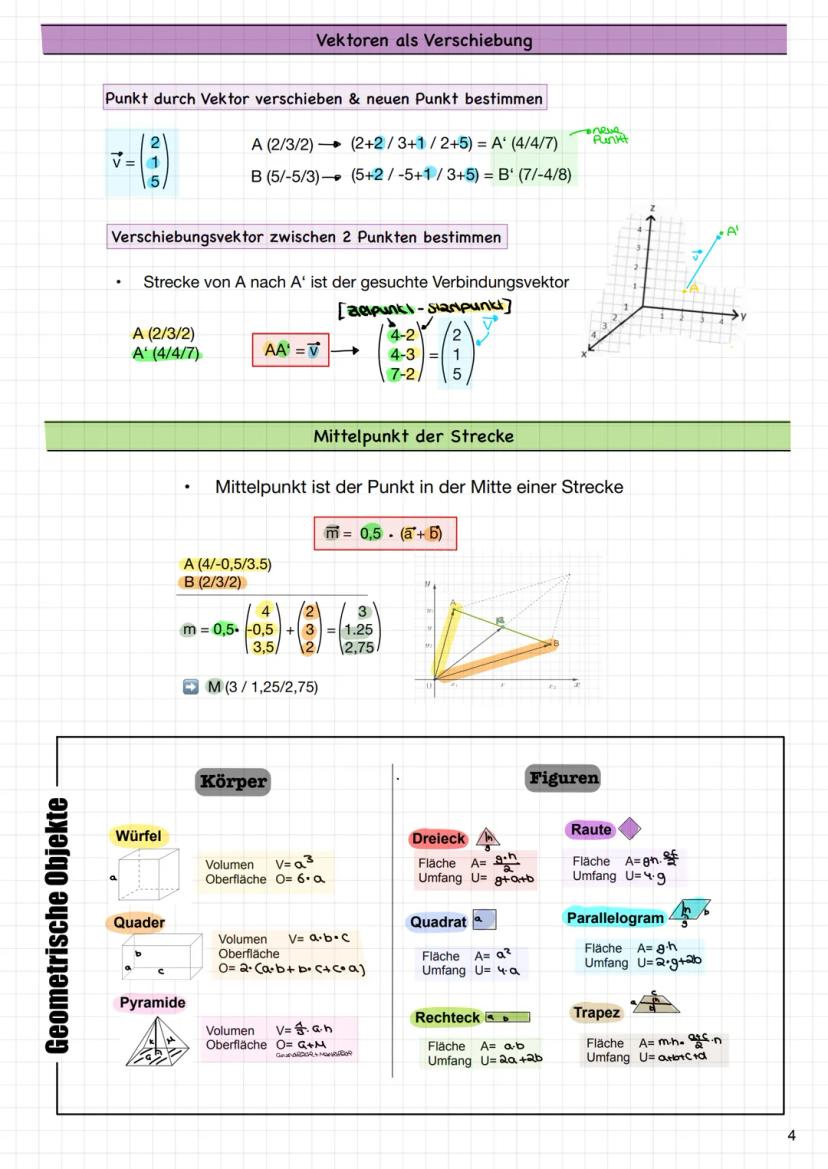
Das Vielfache eines Vektors erhältst du, indem du jede Komponente mit derselben Zahl multiplizierst. Multiplizierst du mit 2, wird der Vektor doppelt so lang. Mit 0,5 wird er halb so lang.
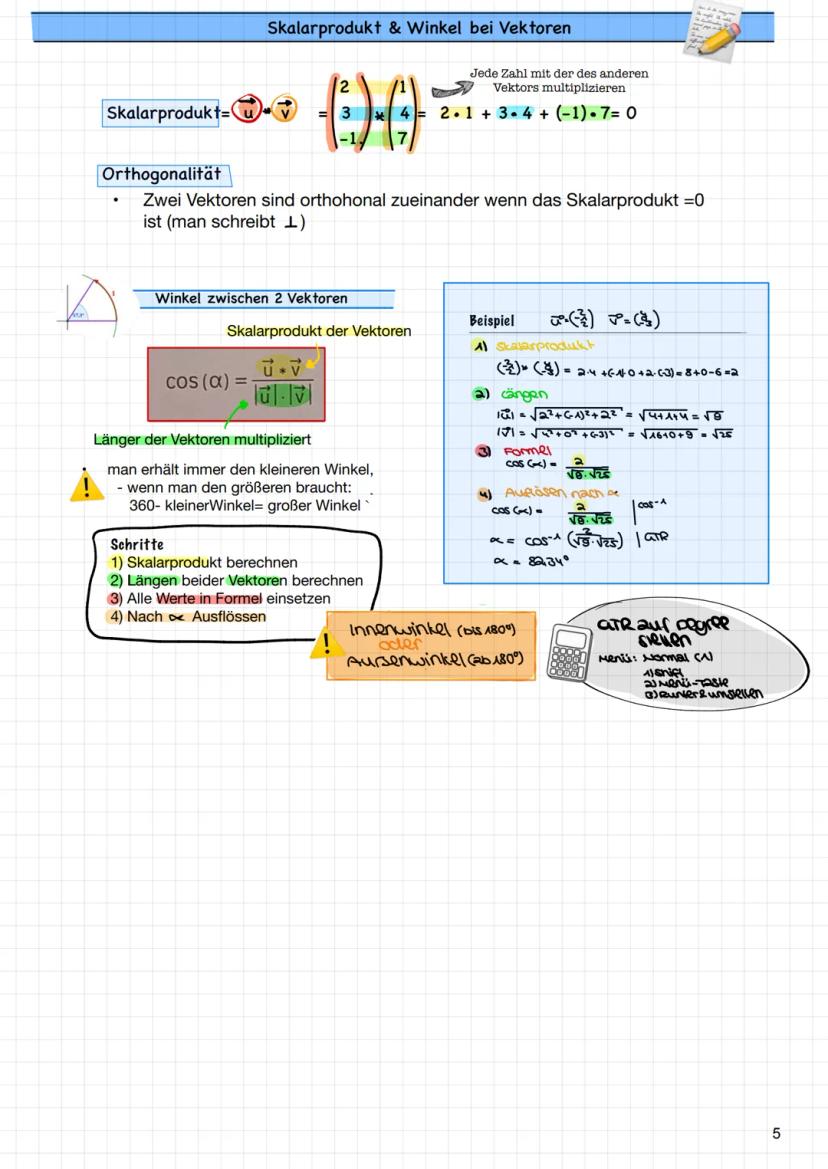
Kollineare Vektoren sind besonders wichtig: Sie sind Vielfache voneinander und liegen auf derselben Geraden. Du erkennst sie, indem du prüfst, ob es eine Zahl r gibt, sodass b⃗ = r·a⃗. Alle drei Komponenten müssen dasselbe r ergeben!
Rechentrick: Wenn du bei der Kollinearitätsprüfung unterschiedliche r-Werte bekommst, sind die Vektoren nicht kollinear!