Wendepunkte und Sattelpunkte
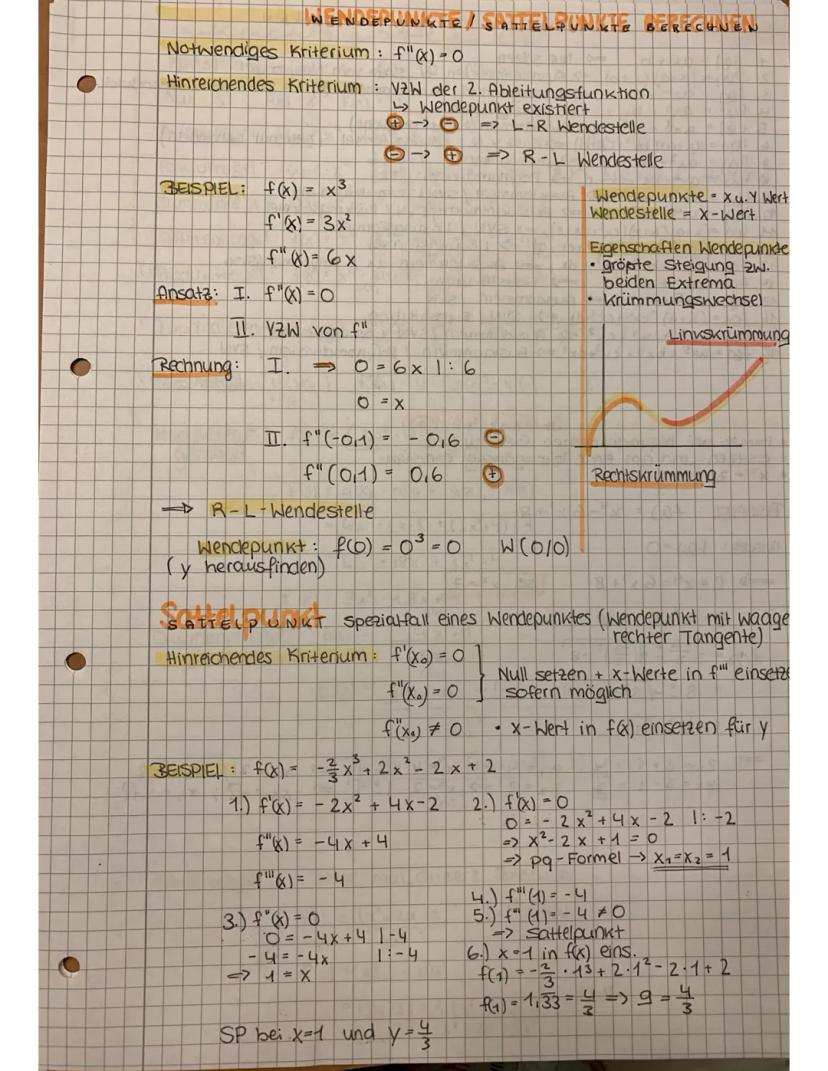
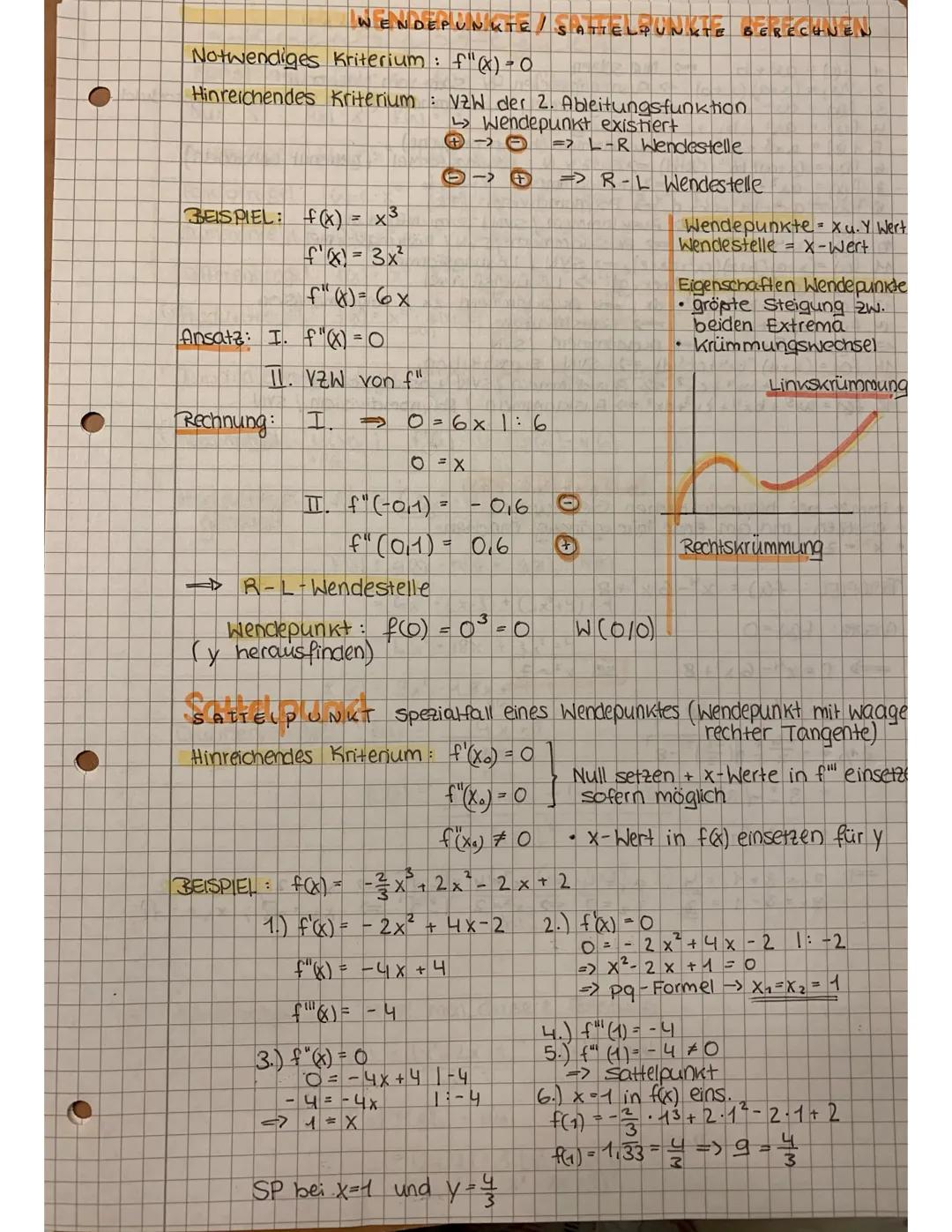
Wendepunkte sind Stellen, wo die Krümmung der Funktion wechselt - von einer Linkskurve zu einer Rechtskurve oder umgekehrt. Das notwendige Kriterium ist f′′(x)=0, das hinreichende prüft den Vorzeichenwechsel der zweiten Ableitung.
Bei einem Vorzeichenwechsel von - nach + hast du eine Links-Rechts-Wendestelle, von + nach - eine Rechts-Links-Wendestelle. Wendepunkte haben oft die größte Steigung zwischen zwei Extrema.
Sattelpunkte sind spezielle Wendepunkte mit waagerechter Tangente. Das erkennst du daran, dass sowohl f′(x0)=0 als auch f′′(x0)=0 gilt. Die Funktion hat dort einen Wendepunkt, aber die Steigung ist null.
Zur Berechnung: Löse f′′(x)=0 für den x-Wert, prüfe den Vorzeichenwechsel und setze den x-Wert in f(x) ein für den y-Wert.
🎢 Anschauung: Wendepunkte sind wie der Übergang von einer Bergfahrt zur Talfahrt auf der Achterbahn!