Extremstellen verstehen und berechnen

Extremstellen sind entweder Hochpunkte (Maxima) oder Tiefpunkte (Minima) einer Funktion. Sie können lokal sein, wenn es in ihrer Umgebung keine höheren/tieferen Punkte gibt, oder global, wenn sie den höchsten/tiefsten Punkt der gesamten Funktion darstellen.

Um Extremstellen zu berechnen, folgst du einem systematischen Verfahren in vier Schritten. Zuerst bestimmst du die erste und zweite Ableitung der Funktion. Dann setzt du die erste Ableitung gleich Null (notwendige Bedingung) und löst nach x auf. Diese x-Werte sind potenzielle Extremstellen.

Im dritten Schritt nutzt du die hinreichende Bedingung: Setze die gefundenen x-Werte in die zweite Ableitung ein. Ist das Ergebnis positiv, handelt es sich um einen Tiefpunkt; ist es negativ, um einen Hochpunkt. Zum Schluss berechnest du die y-Werte, indem du die x-Werte in die Originalfunktion einsetzt.

💡 Merkhilfe: Eine positive zweite Ableitung bedeutet, dass die Funktion nach oben gekrümmt ist – das passt zu einem Tiefpunkt, wo die Funktion "nach oben geht".

Extremstellen-Beispiel

Schauen wir uns ein konkretes Beispiel an: die Funktion f$x$ = x³ - 3x². Um die Extremstellen zu finden, bilden wir zuerst die Ableitungen:

• f'$x$ = 3x² - 6x
• f''$x$ = 6x - 6

Als nächstes suchen wir die Nullstellen der ersten Ableitung (notwendige Bedingung): f'$x$ = 0 3x² - 6x = 0 x$x - 2$ = 0 Das ergibt x₁ = 0 und x₂ = 2 als mögliche Extremstellen.

Jetzt überprüfen wir mit der zweiten Ableitung (hinreichende Bedingung):

• Für x = 0: f''(0) = -6 < 0, also haben wir einen Hochpunkt
• Für x = 2: f''(2) = 6 > 0, also haben wir einen Tiefpunkt

Zum Schluss berechnen wir die y-Koordinaten:

• f(0) = 0 → Hochpunkt bei (0|0)
• f(2) = -4 → Tiefpunkt bei $2|-4$

🔍 Visualisierungstipp: Zeichne die Punkte in ein Koordinatensystem und stelle dir vor, wie die Funktion zwischen ihnen verläuft – der Graph steigt nach dem Tiefpunkt und fällt nach dem Hochpunkt.

Wendepunkte verstehen

Ein Wendepunkt ist eine Stelle, an der die Funktion ihre Krümmungsrichtung ändert – von links nach rechts oder umgekehrt. An diesem Punkt wechselt die zweite Ableitung ihr Vorzeichen.

Das Berechnen von Wendepunkten erfolgt ähnlich wie bei Extremstellen, aber mit einem wichtigen Unterschied. Du benötigst hier die ersten drei Ableitungen der Funktion. Die notwendige Bedingung ist f''$x$ = 0, da wir Punkte suchen, an denen die Krümmung verschwindet.

Bei der hinreichenden Bedingung prüfst du die dritte Ableitung an den potenziellen Wendepunkten. Ist f'''$x$ ≠ 0, liegt tatsächlich ein Wendepunkt vor. Das Vorzeichen der dritten Ableitung zeigt dir zudem die Art der Krümmungsänderung:

• f'''$x$ > 0: Rechts-Links-Krümmung (∩ wird zu ∪)
• f'''$x$ < 0: Links-Rechts-Krümmung (∪ wird zu ∩)

🌀 Visualisierung: Stelle dir einen Wendepunkt wie den Mittelpunkt einer S-Kurve vor – genau hier ändert sich die "Biegung" der Funktion.

Wendepunkt-Beispiel

Betrachten wir die Funktion f$x$ = 0,5x³ - 1,5x². Um den Wendepunkt zu finden, ermitteln wir zunächst die Ableitungen:

• f'$x$ = 1,5x² - 3x
• f''$x$ = 3x - 3
• f'''$x$ = 3

Nun setzen wir die zweite Ableitung gleich Null (notwendige Bedingung): f''$x$ = 0 3x - 3 = 0 x = 1

Der x-Wert 1 ist ein potenzieller Wendepunkt. Zur Überprüfung nutzen wir die hinreichende Bedingung. Da f'''(1) = 3 > 0 ist, handelt es sich um einen Wendepunkt mit Rechts-Links-Krümmung.

Zum Schluss berechnen wir den y-Wert: f(1) = 0,5 · 1³ - 1,5 · 1² = 0,5 - 1,5 = -1

Der Wendepunkt liegt also bei $1|-1$. An diesem Punkt ändert die Funktion ihre Krümmung von nach unten zu nach oben gekrümmt.

📊 Prüfmethode: Teste Punkte links und rechts vom vermuteten Wendepunkt – die zweite Ableitung sollte ihr Vorzeichen wechseln.

Monotonieverhalten von Funktionen

Das Monotonieverhalten beschreibt, wie sich die Funktionswerte verändern, wenn die x-Werte zunehmen. Eine Funktion kann steigend, fallend oder konstant sein.

Bei einer streng monoton steigenden Funktion werden die Funktionswerte größer, wenn die x-Werte zunehmen. Mathematisch ausgedrückt: Wenn x₁ < x₂, dann ist f(x₁) < f(x₂). Beispielsweise ist f$x$ = x² für x > 0 streng monoton steigend.

Im Gegensatz dazu werden bei einer streng monoton fallenden Funktion die Funktionswerte kleiner, wenn die x-Werte zunehmen. Hier gilt: Wenn x₁ < x₂, dann ist f(x₁) > f(x₂). Ein Beispiel hierfür ist f$x$ = -x.

Das Globalverhalten einer Funktion beschreibt, wie sich die Funktion für sehr große oder sehr kleine x-Werte verhält. Dies wird oft durch den führenden Term a·xⁿ bestimmt, wobei a der Koeffizient und n der Exponent ist.

🚀 Praxistipp: Um das Monotonieverhalten schnell zu bestimmen, analysiere das Vorzeichen der ersten Ableitung: Ist f'$x$ > 0, steigt die Funktion; ist f'$x$ < 0, fällt sie.

Globalverhalten von Funktionen

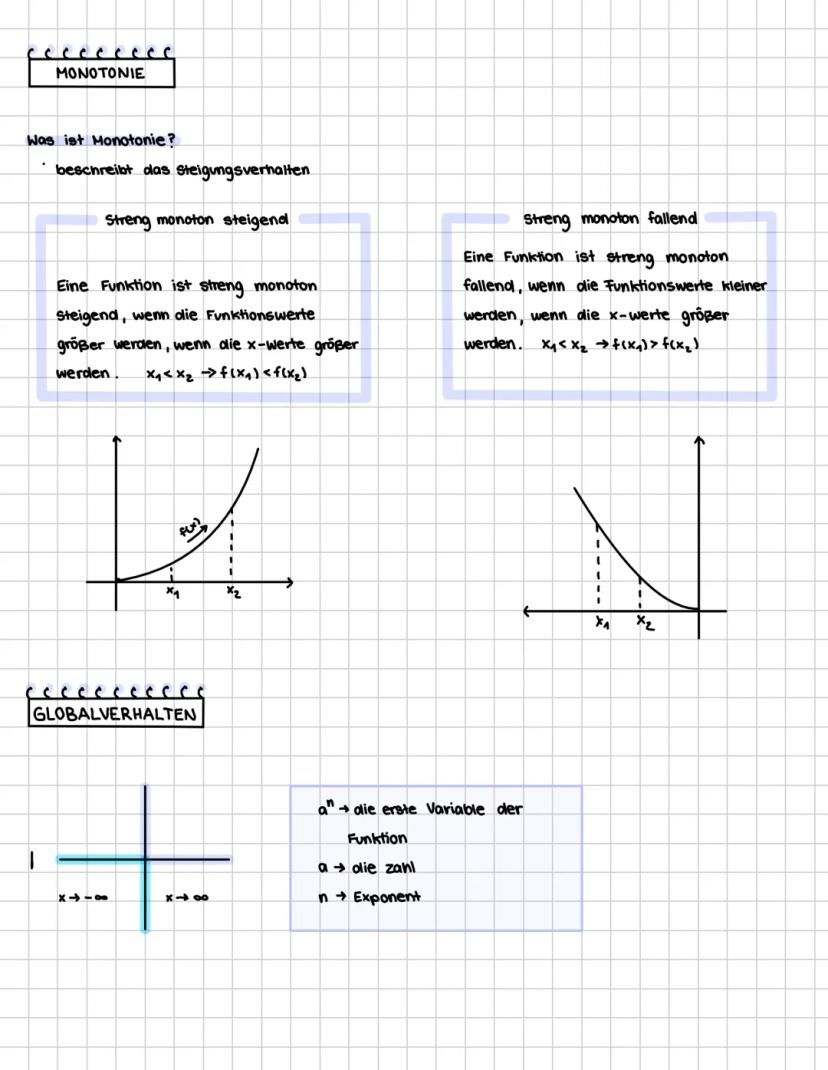
Das Globalverhalten einer Funktion hängt maßgeblich vom führenden Term a·xⁿ ab, wobei sowohl das Vorzeichen von a als auch die Parität (gerade/ungerade) von n entscheidend sind.

Bei Fall 1 (a > 0, n gerade) strebt die Funktion für x → ±∞ gegen +∞. Ein typisches Beispiel ist die Normalparabel f$x$ = x², die für sehr große positive und negative x-Werte immer weiter nach oben steigt.

In Fall 2 (a < 0, n gerade) verhält es sich genau umgekehrt: Die Funktion strebt für x → ±∞ gegen -∞. Beispiel: f$x$ = -x² öffnet sich nach unten.

Bei Fall 3 (a > 0, n ungerade) strebt die Funktion für x → +∞ gegen +∞ und für x → -∞ gegen -∞. Ein klassisches Beispiel ist f$x$ = x³, die links unten beginnt und nach rechts oben verläuft.

In Fall 4 (a < 0, n ungerade) kehrt sich das Verhalten um: Die Funktion strebt für x → +∞ gegen -∞ und für x → -∞ gegen +∞. Beispiel: f$x$ = -x³ verläuft von rechts oben nach links unten.

📈 Anwendungstipp: Das Wissen über das Globalverhalten hilft dir beim Skizzieren von Funktionsgraphen – du weißt sofort, in welche Richtung die "Enden" des Graphen zeigen.