Nullstellen und Extrempunkte
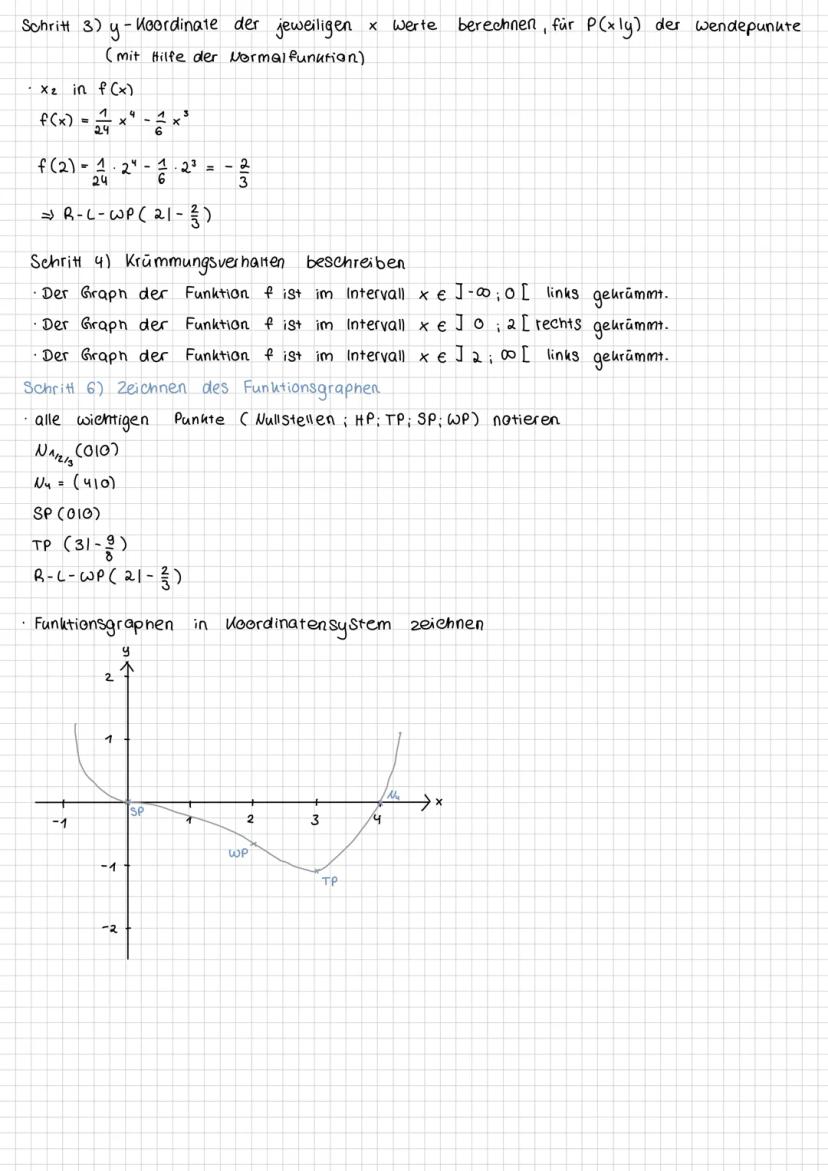
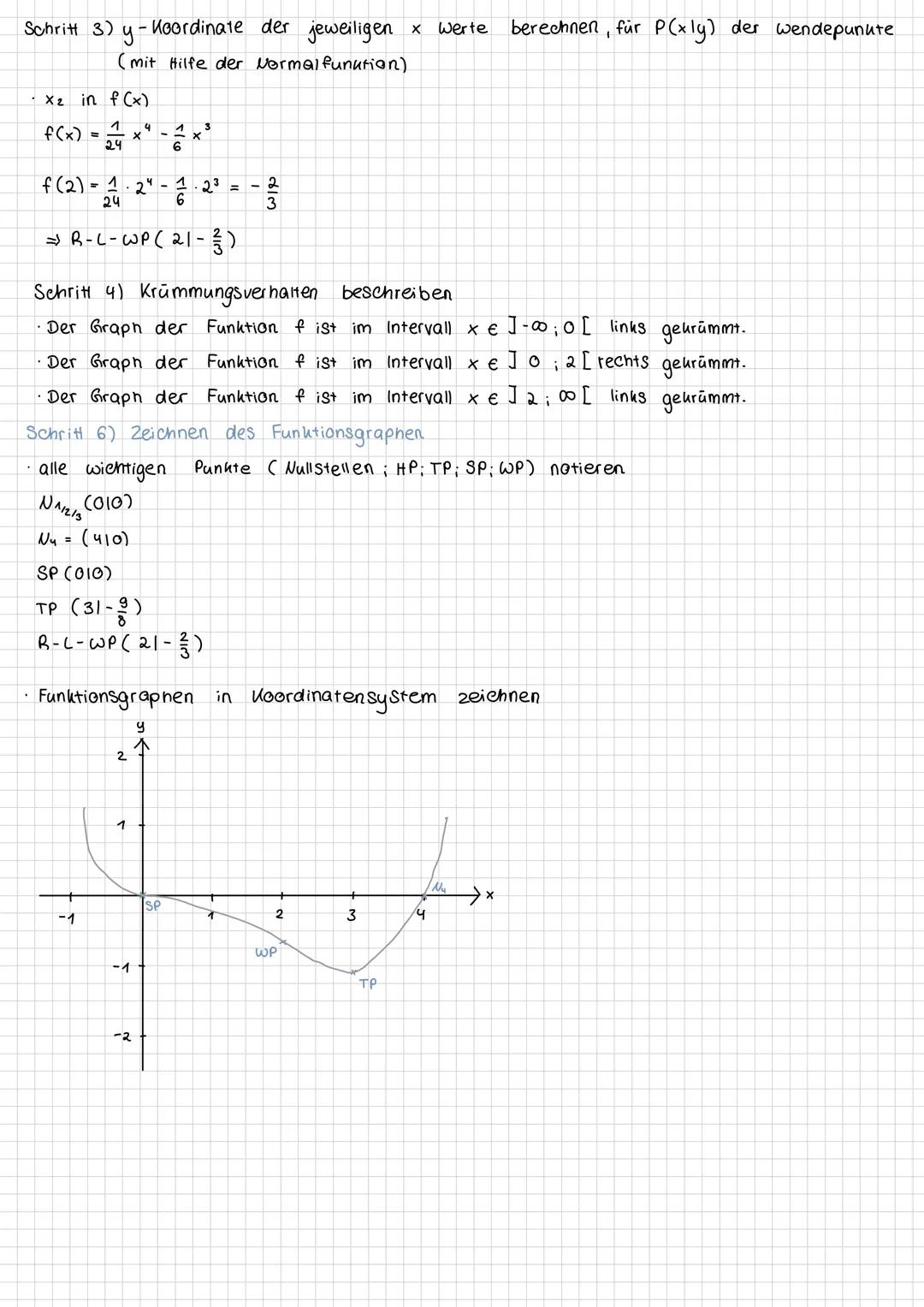
Die Nullstellen findest du durch Lösen der Gleichung f(x) = 0. Bei unserer Funktion erhalten wir x³·(1/24)x−1/6 = 0. Daraus folgen die Nullstellen x₁ = x₂ = x₃ = 0 (dreifache Nullstelle) und x₄ = 4.
Der Schnittpunkt mit der y-Achse liegt bei f(0) = 0, also im Punkt S(0|0).
Für die Extrempunkte benötigen wir die erste Ableitung: f'(x) = (1/6)x³ - (1/2)x². Mit f'(x) = 0 erhalten wir x²·(1/6)x−1/2 = 0, woraus sich x₁ = x₂ = 0 und x₃ = 3 ergeben.
Um festzustellen, ob es sich um Hoch-, Tief- oder Sattelpunkte handelt, bilden wir die zweite Ableitung f''(x) = (1/2)x² - x. Bei f''(0) = 0 liegt ein Sattelpunkt vor, während f''(3) = 1,5 > 0 einen Tiefpunkt anzeigt. Der Tiefpunkt liegt bei TP(3|-9/8).
Wichtig: Bei f''(x) = 0 musst du zusätzlich prüfen, ob ein Extrempunkt oder Wendepunkt vorliegt. Häufig handelt es sich um einen Sattelpunkt, wie in unserem Beispiel bei x = 0.